Difference between revisions of "CSC270 Exercises on FSM"
(→Exercise #1) |
|||
| Line 68: | Line 68: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | <br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Line 74: | Line 75: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | <br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Line 81: | Line 83: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<code><pre> | <code><pre> | ||
# flipflop.py | # flipflop.py | ||
| Line 164: | Line 146: | ||
19 1 1 1 | 19 1 1 1 | ||
| − | + | ||
<br /> | <br /> | ||
Revision as of 15:55, 2 March 2011
--D. Thiebaut 15:24, 28 February 2011 (EST)
Exercise #1
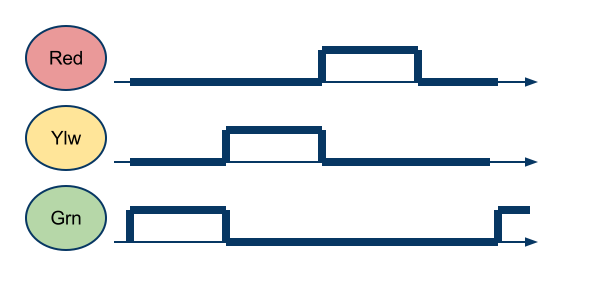
- Implement a sequencer (FSM) which activates 3 Lights: a green light, a yellow light, and a red light. The behavior of the FSM is the following:
- the green light stays on for 30 seconds, then
- the yellow light comes on and stays on for 30 seconds, then
- the red light comes on and stays on for 30 seconds, then we repeat the pattern.
- There is only one light on at a given time.
- What is the frequency of your clock signal?
Exercise #2
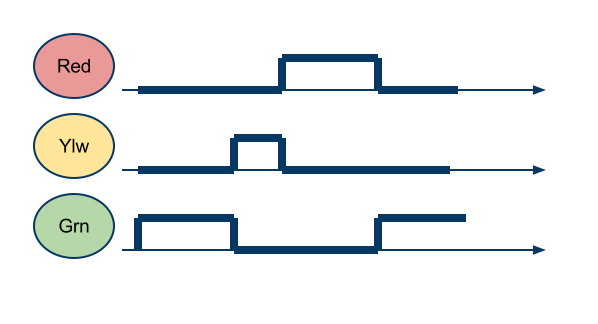
- Same as Exercise 1, but this time the behavior is the following
- the green light comes on after the red light and stays on for 30 seconds,
- the yellow light comes on and stays on for the next for 15 seconds,
- the red light comes on after the yellow light for 30 seconds.
- What is the frequency of your clock signal?
Exercise #3
- Create a "true" frequency divider that divides by 4.
Exercise #4
- What is the state diagram of the 3-flip-flop circuit with the following equations:
D0 = Q0'
D1 = Q0 XOR Q1
D2 = Q1 XOR Q2
Exercise #5
- Same question, but solve it with Python.
# flipflop.py
# implements a simple sequencer
#
def xor( a, b ):
if ( a==b ):
return 0
return 1
def main():
# assume we start in a state where all 3 flip-flops are outputing 0
D0 = 0
D1 = 0
D2 = 0
for t in range( 20 ):
Q0 = D0
Q1 = D1
Q2 = D2
if t==0:
print "%2s %2s %2s %2s" % ( "t", "Q0", "Q1", "Q2" )
print "----|------------"
print "%2d %2d %2d %2d" % ( t, Q0, Q1, Q2 )
D0 = 1 - Q0
D1 = xor( Q0, Q1 )
D2 = xor( Q1, Q2 )
main()
;Output
t Q0 Q1 Q2
|------------
0 0 0 0
1 1 0 0
2 0 1 0
3 1 1 1
4 0 0 0
5 1 0 0
6 0 1 0
7 1 1 1
8 0 0 0
9 1 0 0
10 0 1 0
11 1 1 1
12 0 0 0
13 1 0 0
14 0 1 0
15 1 1 1
16 0 0 0
17 1 0 0
18 0 1 0
19 1 1 1