Difference between revisions of "CSC231 Exercises with Signed Numbers"

From dftwiki3
Jump to: navigation, search
(→‎Binary Addition in Various Systems)
(→‎Exercise 1)
Line 16: Line 16:
  
 
<br />
 
<br />
 +
=Problem #2=
 +
 +
* what is the 8-bit representation of the following '''decimal''' numbers in signed magnitude, 1's complement, and 2's complement?
 +
 +
0
 +
 +
 
 +
1
 +
 +
 
 +
-1
 +
 +
 +
11
 +
 +
 +
-11
 +
 +
 +
127
 +
 +
 +
-127
 +
   
 +
 +
128
 +
 +
 +
-128
 +
 +
 +
=Problem #3=
 +
 +
* Convert the following signed, 2's complement 16-bit binary numbers to their decimal equivalent.
 +
 +
 +
  0000 0000 0000 0001
 +
 +
  1000 0000 0000 0001
 +
 +
  0000 0000 1111 1111
 +
 +
  1111 1111 1111 1111
 +
 +
=Problem #4=
 +
 +
* Perform the binary addition of the following '''decimal''' numbers using 2's complement, and assuming the numbers are 16-bit words
 +
 +
::(for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary)
 +
 +
  23 - 100 =
 +
 +
  23 - 23 =
 +
 +
100 - 23 =
 +
 +
 +
<br />
 +
<br />
 +
<br />
 +
<br />
 +
<br />
 +
<br />
 +
<br />
 +
<br />
 +
<br />
 +
<br />
 +
 +
=Solutions=
 +
<onlydft>
 +
==Problem #1==
 +
 +
0 = 0000 0000 in all 3 systems
 +
 +
1 = 0000 0001 in all 3 systems
 +
 +
-1 = 1000 0001 in signed magnitude
 +
    = 1111 1110 in 1's complement
 +
    = 1111 1111 in 2's complement
 +
 +
11 = 0001 0011 in all 3 systems
 +
 
 +
-11 = 1001 0011 in signed magnitude
 +
      = 1110 1100 in 1's complement
 +
      = 1110 1101 in 2's complement
 +
 +
127 = 0111 1111 in all 3 systems
 +
 +
-127 = 1111 1111 in s.m.
 +
        = 1000 0000 in 1's complement
 +
        = 1000 0001 in 2's complement
 +
 +
128 = 1000 0000 in s.m., but that would make it negative ==> can't represent 128 in s.m.
 +
      = 1000 0000 in 1's complement, but, again, that's not possible ==> can't represent 128 in 1's complement
 +
      = 1000 0000 in 2's complement, but, again, that's not possible ==> can't represent 128 in 2's complement
 +
 +
==Problem #2==
 +
 +
  0000 0000 0000 0001  = 1
 +
 +
  1000 0000 0000 0001  is the opposite of 0111 1111 1111 1110 + 1 which is 0111 1111 1111 1111
 +
                                  which is 7FFF = 32767 decimal.  The number is therefore the representation
 +
                                  of -327676
 +
 +
  0000 0000 1111 1111 is +255 in decimal
 +
 +
  1111 1111 1111 1111 is the opposite of 0000 0000 0000 0000 + 1 = 0000 0000 0000 0001 which is 1.
 +
                                  The all-1 bit pattern is therefore the representation of -1
 +
 +
==Problem #3==
 +
 +
::(for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary)
 +
 +
  23 - 100 =  0001 0111 - 0110 0100 
 +
              =  0001 0111 + ( 1001 1011 + 1 )             
 +
              =  0001 0111 + 1001 1100 = 1011 0011 which is negative.
 +
              this result is the opposite of 0100 1101, which is 64 + 8 + 4 + 1 = 77
 +
              the result must be -77.  It works!
 +
 
 +
  23 - 23 = 0001 0111 - 0001 0111
 +
            = 0001 0111 + ( 1110 1000 + 1 )
 +
            = 0001 0111 + ( 1110 1001 )
 +
            = 0000 0000 (there's a carry that is lost)
 +
            this is 0.  Again, it works!
 +
 +
100 - 23 = 0110 0100 - 0001 0111
 +
              = 0110 0100 + ( 1110 1000 + 1 )
 +
              = 0110 0100 + 1110 1001
 +
              = 0100 1101 (and a carry that is lost)
 +
              = 77.  It works!
 +
 +
 +
</onlydft>
  
 
<br />
 
<br />

Revision as of 08:42, 1 October 2012

--D. Thiebaut 09:37, 1 October 2012 (EDT)


Binary Addition in Various Systems

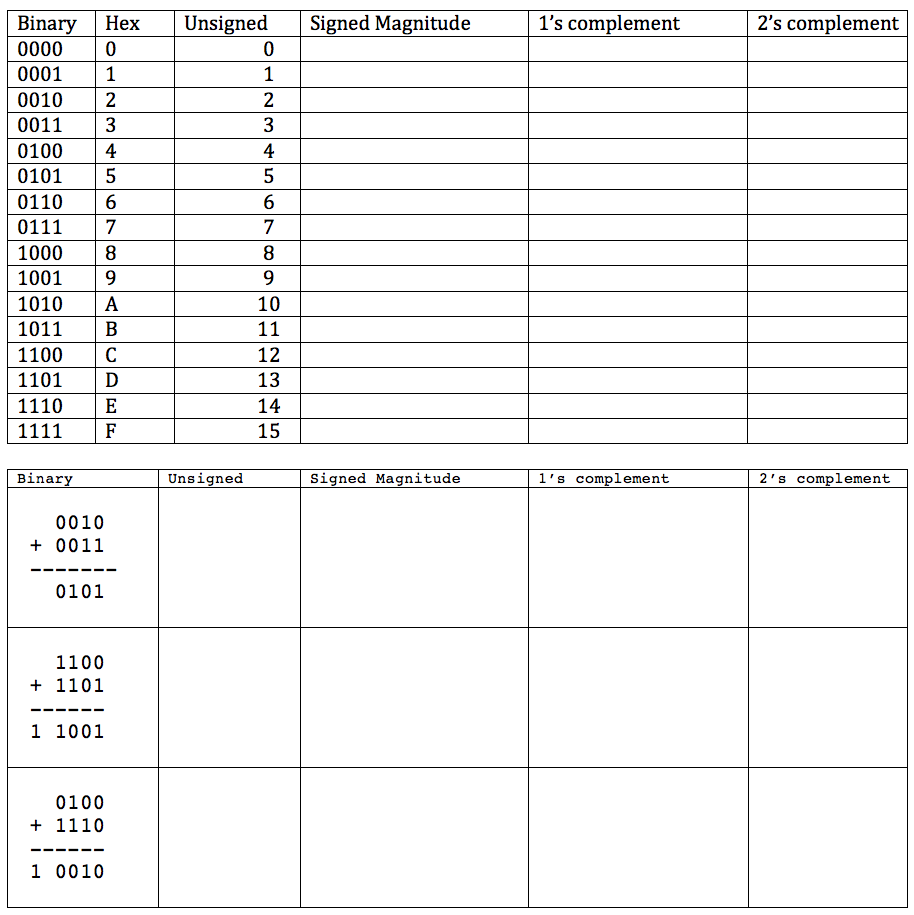
CSC231TableSignedNumbers.png



Exercise 1

An program written in some unspecified language contains an array of 10 bytes. The values of the 10 bytes are 0x10, 0xff, 0xf1, 0x00, 0x00, 0xfe, 0x73, 0x01, 0x02, 0x7f.

Are these values used to represent signed numbers, unsigned numbers, numbers in 2's complement, numbers in 1's complement, or numbers in signed magnitude?



Problem #2

  • what is the 8-bit representation of the following decimal numbers in signed magnitude, 1's complement, and 2's complement?
0

 
1

 
-1 


11


-11


127


-127
   

128


-128

Problem #3

  • Convert the following signed, 2's complement 16-bit binary numbers to their decimal equivalent.


 0000 0000 0000 0001

 1000 0000 0000 0001

 0000 0000 1111 1111

 1111 1111 1111 1111

Problem #4

  • Perform the binary addition of the following decimal numbers using 2's complement, and assuming the numbers are 16-bit words
(for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary)
 23 - 100 =

 23 - 23 =

100 - 23 =












Solutions


...








Retrieved from "http://dominiquethiebaut.com/dftwiki3/index.php?title=CSC231_Exercises_with_Signed_Numbers&oldid=15250"