Difference between revisions of "CSC231 Exercises with Signed Numbers"
(→Exercise 1) |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 77: | Line 77: | ||
| + | =Exercise 6= | ||
| + | * Before doing this exercise, we need to play with these two programs: | ||
| + | ** Playing with int overflow in java: [[CSC231 MultBy3.java Program| MultBy3.java]] | ||
| + | ** Same with Python: [[CSC231 multBy3.py Program | multBy3.py]] | ||
| + | * A badly written software program is supposed to monitor and display the temperature recorded by a thermometer. This thermometer is used in chemical beaker. During an important experiment, the display outputs the following values: | ||
| + | |||
| + | ::56 59 70 81 99 110 -125 | ||
| + | |||
| + | * What was the most likely true value of the last temperature recorded? | ||
| + | * (For reference, 125 in binary is 0111 1101, and -125 in 2's complement is 1000 0011.) | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Line 89: | Line 99: | ||
=Solutions= | =Solutions= | ||
| − | + | ||
==Problem #1== | ==Problem #1== | ||
| + | |||
| + | * What is the range of numbers in a 4-bit unsigned system? in a 4-bit 2's complement system? in an 8-bit unsigned system? In an 8-bit 2's complement system? | ||
| + | |||
| + | * 4-bit unsigned: from 0 to 2<sup>4</sup>-1, or 0-15 | ||
| + | * 4-bit 2's complement: from -2<sup>4-1</sup> to 2<sup>4-1</sup>-1, or -8 to +7. | ||
| + | * 8-bit unsigned: from 0 to <sup>8</sup>-1, or 0 to 255 | ||
| + | * 8-bit 2's complement: from -2<sup>8-1</sup> to 2<sup>8-1</sup>-1, or -128 to +127. | ||
| + | |||
| + | ==Problem #2== | ||
| + | |||
| + | There is no way you can tell. It all depends on what the programmer intends to do with the data, and how she declares these numbers. So, no, you can't tell! | ||
| + | |||
| + | ==Problem #3== | ||
0 = 0000 0000 in all 3 systems | 0 = 0000 0000 in all 3 systems | ||
| Line 116: | Line 139: | ||
= 1000 0000 in 2's complement, but, again, that's not possible ==> can't represent 128 in 2's complement | = 1000 0000 in 2's complement, but, again, that's not possible ==> can't represent 128 in 2's complement | ||
| − | ==Problem # | + | ==Problem #4== |
0000 0000 0000 0001 = 1 | 0000 0000 0000 0001 = 1 | ||
| Line 129: | Line 152: | ||
The all-1 bit pattern is therefore the representation of -1 | The all-1 bit pattern is therefore the representation of -1 | ||
| − | ==Problem # | + | ==Problem #5== |
::(for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary) | ::(for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary) | ||
| Line 151: | Line 174: | ||
= 77. It works! | = 77. It works! | ||
| + | ==Problem #6== | ||
| − | + | * 125 is 0111 1101. | |
| + | * -125 is 1000 0011 | ||
| + | * In 2's complement, the most significant bit of an 8-bit word has weight -128. Why? Because 1000 0000 is -128 in 2's complement. So when we see -125, it's really the result of saying "these bits represent -128 + 3. But if this were an unsigned number, the value would be +128 + 3 = 131. Another way of saying this, is that if we add 256 to -125, we get 131. So, very likely, the temperature we should have see is 131 degrees. | ||
| + | |||
<br /> | <br /> | ||
Latest revision as of 14:19, 4 October 2012
--D. Thiebaut 09:37, 1 October 2012 (EDT)
Binary Addition in Various Systems
Exercise 1
What is the range of numbers in a 4-bit unsigned system? in a 4-bit 2's complement system? in an 8-bit unsigned system? In an 8-bit 2's complement system?
(Revisit the handout on Java's range of data types.)
Exercise 2
An program written in some unspecified language contains an array of 10 bytes. The values of the 10 bytes are 0x10, 0xff, 0xf1, 0x00, 0x00, 0xfe, 0x73, 0x01, 0x02, 0x7f.
Are these values used to represent signed numbers, unsigned numbers, numbers in 2's complement, numbers in 1's complement, or numbers in signed magnitude?
Exercise 3
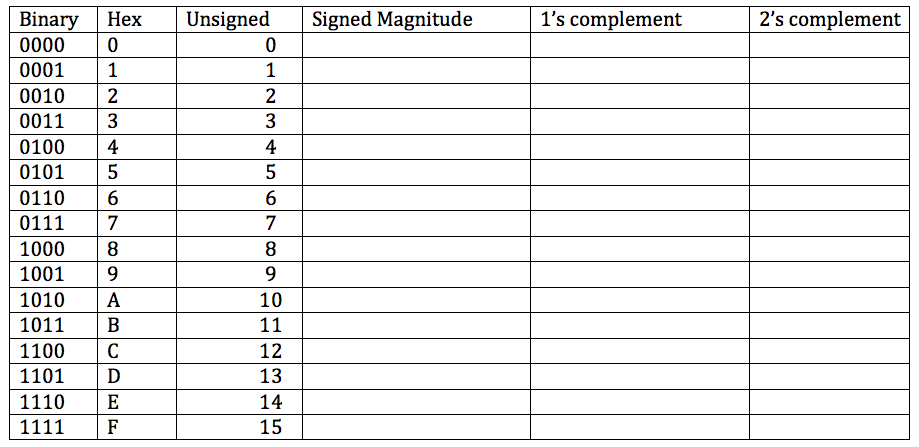
- what is the 8-bit representation of the following decimal numbers in signed magnitude, 1's complement, and 2's complement?
0 1 -1 11 -11 127 -127 128 -128
Exercise #4
- Convert the following signed, 2's complement 16-bit binary numbers to their decimal equivalent.
0000 0000 0000 0001 1000 0000 0000 0001 0000 0000 1111 1111 1111 1111 1111 1111
Exercise 5
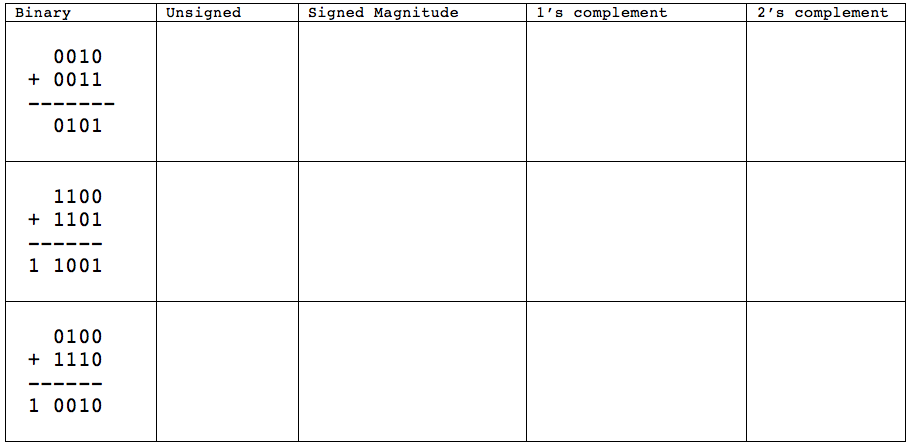
- Perform the binary addition of the following decimal numbers using 2's complement, and assuming the numbers are 16-bit words
- (for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary)
23 - 100 = 23 - 23 = 100 - 23 =
Exercise 6
- Before doing this exercise, we need to play with these two programs:
- Playing with int overflow in java: MultBy3.java
- Same with Python: multBy3.py
- A badly written software program is supposed to monitor and display the temperature recorded by a thermometer. This thermometer is used in chemical beaker. During an important experiment, the display outputs the following values:
- 56 59 70 81 99 110 -125
- What was the most likely true value of the last temperature recorded?
- (For reference, 125 in binary is 0111 1101, and -125 in 2's complement is 1000 0011.)
Solutions
Problem #1
- What is the range of numbers in a 4-bit unsigned system? in a 4-bit 2's complement system? in an 8-bit unsigned system? In an 8-bit 2's complement system?
- 4-bit unsigned: from 0 to 24-1, or 0-15
- 4-bit 2's complement: from -24-1 to 24-1-1, or -8 to +7.
- 8-bit unsigned: from 0 to 8-1, or 0 to 255
- 8-bit 2's complement: from -28-1 to 28-1-1, or -128 to +127.
Problem #2
There is no way you can tell. It all depends on what the programmer intends to do with the data, and how she declares these numbers. So, no, you can't tell!
Problem #3
0 = 0000 0000 in all 3 systems
1 = 0000 0001 in all 3 systems
-1 = 1000 0001 in signed magnitude
= 1111 1110 in 1's complement
= 1111 1111 in 2's complement
11 = 0001 0011 in all 3 systems
-11 = 1001 0011 in signed magnitude
= 1110 1100 in 1's complement
= 1110 1101 in 2's complement
127 = 0111 1111 in all 3 systems
-127 = 1111 1111 in s.m.
= 1000 0000 in 1's complement
= 1000 0001 in 2's complement
128 = 1000 0000 in s.m., but that would make it negative ==> can't represent 128 in s.m.
= 1000 0000 in 1's complement, but, again, that's not possible ==> can't represent 128 in 1's complement
= 1000 0000 in 2's complement, but, again, that's not possible ==> can't represent 128 in 2's complement
Problem #4
0000 0000 0000 0001 = 1
1000 0000 0000 0001 is the opposite of 0111 1111 1111 1110 + 1 which is 0111 1111 1111 1111
which is 7FFF = 32767 decimal. The number is therefore the representation
of -327676
0000 0000 1111 1111 is +255 in decimal
1111 1111 1111 1111 is the opposite of 0000 0000 0000 0000 + 1 = 0000 0000 0000 0001 which is 1.
The all-1 bit pattern is therefore the representation of -1
Problem #5
::(for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary)
23 - 100 = 0001 0111 - 0110 0100
= 0001 0111 + ( 1001 1011 + 1 )
= 0001 0111 + 1001 1100 = 1011 0011 which is negative.
this result is the opposite of 0100 1101, which is 64 + 8 + 4 + 1 = 77
the result must be -77. It works!
23 - 23 = 0001 0111 - 0001 0111
= 0001 0111 + ( 1110 1000 + 1 )
= 0001 0111 + ( 1110 1001 )
= 0000 0000 (there's a carry that is lost)
this is 0. Again, it works!
100 - 23 = 0110 0100 - 0001 0111
= 0110 0100 + ( 1110 1000 + 1 )
= 0110 0100 + 1110 1001
= 0100 1101 (and a carry that is lost)
= 77. It works!
Problem #6
- 125 is 0111 1101.
- -125 is 1000 0011
- In 2's complement, the most significant bit of an 8-bit word has weight -128. Why? Because 1000 0000 is -128 in 2's complement. So when we see -125, it's really the result of saying "these bits represent -128 + 3. But if this were an unsigned number, the value would be +128 + 3 = 131. Another way of saying this, is that if we add 256 to -125, we get 131. So, very likely, the temperature we should have see is 131 degrees.