Difference between revisions of "CSC103 Homework 2 Solution 2013"
(Created page with "--~~~~ ---- =Logic Design Problem= <center>Image:CSC103Homework2Prob1Sol.png</center> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br ...") |
|||
| Line 2: | Line 2: | ||
---- | ---- | ||
| − | =Logic Design Problem= | + | =Logic Design Problem (2 points)= |
| + | |||
| + | The truth table was worth 1 point. | ||
<center>[[Image:CSC103Homework2Prob1Sol.png]]</center> | <center>[[Image:CSC103Homework2Prob1Sol.png]]</center> | ||
| + | |||
| + | You had two options. One was to list all 11 terms corresponding to the 11 True symbols in the last column of the table, and or them together. The other was to take the expression directly from the diagram, which resulted in a much simpler formula. | ||
| + | |||
| + | The first method yielded (I'll list on the first and last of the 11 terms): | ||
| + | |||
| + | f = ( NOT a AND NOT b AND NOT c AND NOT d ) OR ... OR ( a AND b AND c and NOT d ) | ||
| + | |||
| + | The second method yielded: | ||
| + | |||
| + | f = NOT ( ( a AND b ) OR (not c ) AND d ) | ||
| + | |||
| + | The correct expression for f, which ever method was used was worth 1 point. | ||
| + | |||
| + | =LOGIC SIMULATOR (3 points)= | ||
| + | |||
| + | f = ( ( NOT a ) AND b AND ( NOT c ) ) | ||
| + | OR ( a AND ( NOT b ) AND c ) | ||
| + | OR ( a AND b AND ( NOT c ) ) | ||
| + | |||
| + | <center>[[Image:CSC103_HW2_2013_Circuit.png|500px]]</center> | ||
| + | <br /> | ||
<br /> | <br /> | ||
Latest revision as of 12:05, 25 September 2013
--D. Thiebaut (talk) 10:39, 25 September 2013 (EDT)
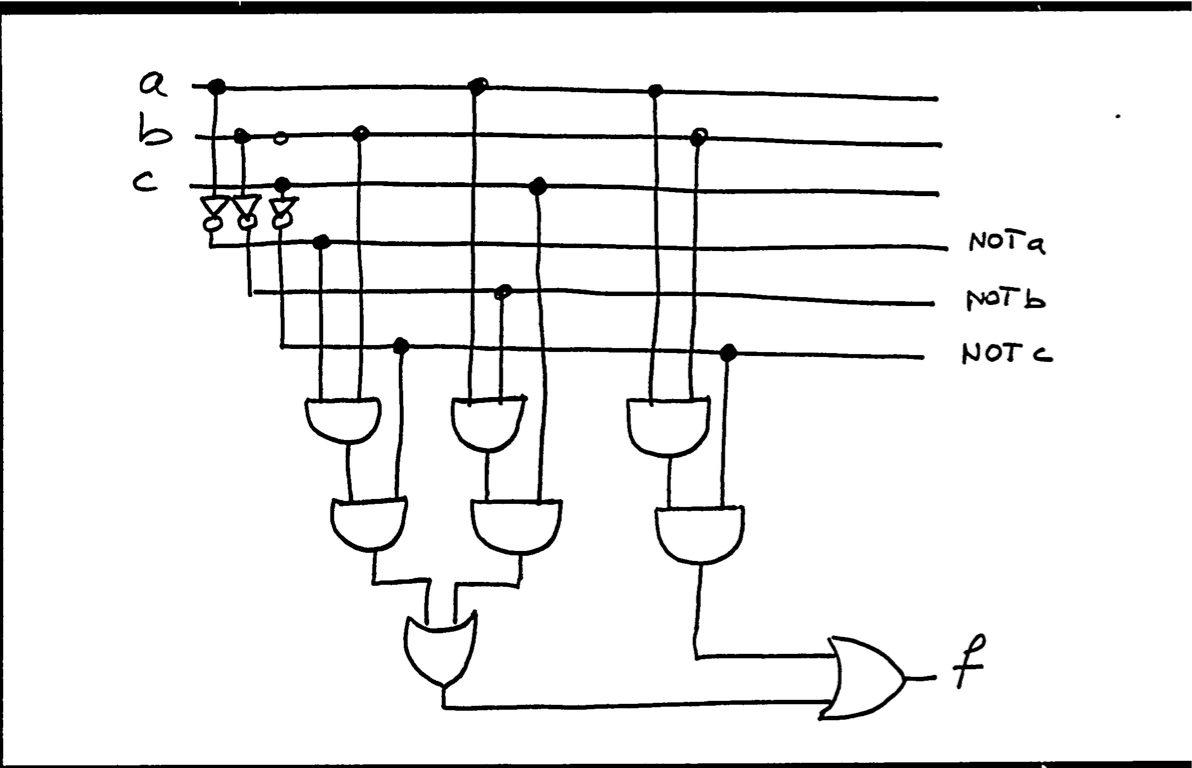
Logic Design Problem (2 points)
The truth table was worth 1 point.
You had two options. One was to list all 11 terms corresponding to the 11 True symbols in the last column of the table, and or them together. The other was to take the expression directly from the diagram, which resulted in a much simpler formula.
The first method yielded (I'll list on the first and last of the 11 terms):
f = ( NOT a AND NOT b AND NOT c AND NOT d ) OR ... OR ( a AND b AND c and NOT d )
The second method yielded:
f = NOT ( ( a AND b ) OR (not c ) AND d )
The correct expression for f, which ever method was used was worth 1 point.
LOGIC SIMULATOR (3 points)
f = ( ( NOT a ) AND b AND ( NOT c ) ) OR ( a AND ( NOT b ) AND c ) OR ( a AND b AND ( NOT c ) )