Difference between revisions of "CSC111 FractalTree.py"
(Created page with "--~~~~ ---- <br /> =Fractal Tree= <br /> <source lang="python"> # practalTree.py # D. Thiebaut # Code taken from http://openbookproject.net/thinkcs/python/english3e/recursion....") |
|||
| Line 2: | Line 2: | ||
---- | ---- | ||
<br /> | <br /> | ||
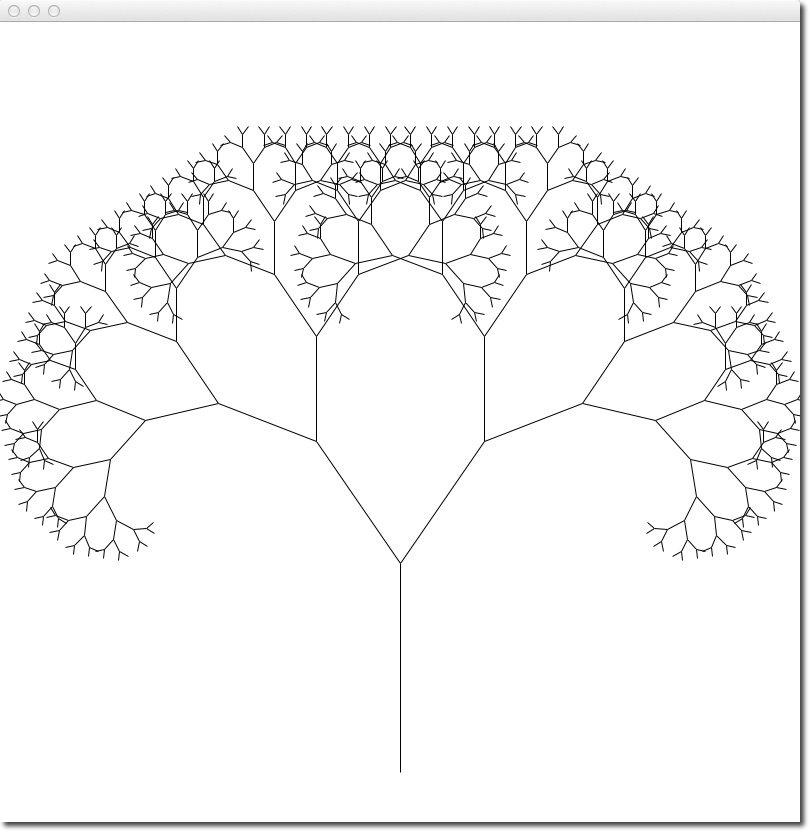
| + | [[Image:FractalTree.png|right|250px]] | ||
=Fractal Tree= | =Fractal Tree= | ||
<br /> | <br /> | ||
| Line 58: | Line 59: | ||
win = GraphicsWindow(MAXWIDTH, MAXHEIGHT) | win = GraphicsWindow(MAXWIDTH, MAXHEIGHT) | ||
canvas = win.canvas() | canvas = win.canvas() | ||
| − | theta = 0. | + | theta = 0.01 # use 0.02 for tall skinny trees, 0.7 for fat trees |
draw_tree(canvas, | draw_tree(canvas, | ||
9, | 9, | ||
Revision as of 07:48, 29 April 2014
--D. Thiebaut (talk) 07:45, 29 April 2014 (EDT)
Fractal Tree
# practalTree.py
# D. Thiebaut
# Code taken from http://openbookproject.net/thinkcs/python/english3e/recursion.html
# and adapted to work with graphics111.py.
#
# Draws a fractal tree on the graphic window.
#
from graphics111 import *
import math
import time
import random
# dimensions of the window
MAXWIDTH = 800
MAXHEIGHT = 800
# recursive tree-drawing function
#
def draw_tree(canvas, # the canvas
order, # the level of recursion. Starts positive.
theta, # angle of new branch leaving this trunk
sz, # size of this branch
x, y, # coordinates of base of this branch
heading # angle of direction of this branch
):
trunk_ratio = 0.29 # How big is the trunk relative to whole tree?
trunk = sz * trunk_ratio # length of trunk
# compute x, y of end of the current branch
delta_x = trunk * math.cos(heading)
delta_y = trunk * math.sin(heading)
x2, y2 = x + delta_x, y + delta_y
# draw current branch
canvas.setFill( 0,0,0 )
canvas.drawLine(x, y, x2, y2)
# if this branch has sub-branches, then recurse
if order > 0:
# make the recursive calls to draw the two subtrees
newsz = sz*(1 - trunk_ratio)
draw_tree(canvas,
order-1, theta, newsz, x2, y2, heading-theta )
draw_tree(canvas,
order-1, theta, newsz, x2, y2, heading+theta )
# draw 1 tree in the middle of the screen, shooting straight up.
def main():
win = GraphicsWindow(MAXWIDTH, MAXHEIGHT)
canvas = win.canvas()
theta = 0.01 # use 0.02 for tall skinny trees, 0.7 for fat trees
draw_tree(canvas,
9,
theta,
MAXWIDTH*0.9, MAXWIDTH//2,
MAXHEIGHT-50,
-math.pi/2)
win.wait()
win.close()
main()