Difference between revisions of "CSC270 Homework 1"
(→Problem 1) |
(→Problem 1) |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
(c) --[[User:Thiebaut|D. Thiebaut]] 22:01, 28 January 2009 (UTC) | (c) --[[User:Thiebaut|D. Thiebaut]] 22:01, 28 January 2009 (UTC) | ||
<br /> | <br /> | ||
| − | [CSC270 | Back ] to Main Page | + | [[CSC270 | Back ]] to Main Page |
---- | ---- | ||
| Line 13: | Line 13: | ||
{| border="1" cellpadding="2" | {| border="1" cellpadding="2" | ||
| − | ! x | + | ! x |
| − | ! y | + | ! y |
| − | ! x U y | + | ! x U y |
|- | |- | ||
| | | | ||
| Line 21: | Line 21: | ||
| | | | ||
α | α | ||
| − | | | + | | |
α | α | ||
|- | |- | ||
| Line 27: | Line 27: | ||
α | α | ||
| | | | ||
| − | & | + | β |
| | | | ||
α | α | ||
|- | |- | ||
| | | | ||
| − | & | + | β |
| | | | ||
α | α | ||
| Line 39: | Line 39: | ||
|- | |- | ||
| | | | ||
| − | & | + | β |
| | | | ||
| − | & | + | β |
| | | | ||
β | β | ||
| Line 50: | Line 50: | ||
{| border="1" cellpadding="2" | {| border="1" cellpadding="2" | ||
| − | ! x | + | ! x |
| − | ! y | + | ! y |
| − | ! x T y | + | ! x T y |
|- | |- | ||
| | | | ||
| Line 64: | Line 64: | ||
α | α | ||
| | | | ||
| − | & | + | β |
| | | | ||
β | β | ||
|- | |- | ||
| | | | ||
| − | & | + | β |
| | | | ||
α | α | ||
| Line 76: | Line 76: | ||
|- | |- | ||
| | | | ||
| − | & | + | β |
| | | | ||
| − | & | + | β |
| | | | ||
β | β | ||
|} | |} | ||
| + | |||
| + | <br /><br /> | ||
| + | Which of these assertions is true? | ||
| + | * α is 1, β is 0, '''U''' is the AND operator, and '''T''' the OR operator | ||
| + | * α is 0, β is 1, '''U''' is the OR operator, and '''T''' is the AND operator | ||
| + | |||
| + | Be sure to explain why one assertion is true, or why it is false! | ||
| + | |||
| + | =Problem 2= | ||
| + | |||
| + | Expand and simplify the function defined as f(a, b, c, d ) = Σ(0, 1, 2, 8, 10, 12, 13, 14, 15) | ||
| + | |||
| + | Expand and simplify the function defined as g(a, b, c, d ) = Σ( 3, 4, 5, 6, 7, 9, 11 ) | ||
| + | |||
| + | |||
| + | Make sure you use your head and think!!! | ||
| + | |||
| + | =Problem 3= | ||
| + | |||
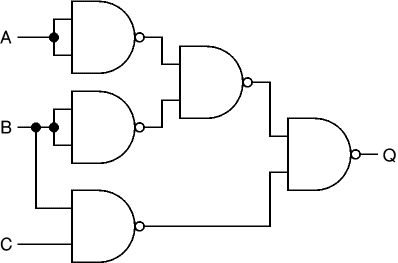
| + | [[Image:CSC270_gates3.gif | right]] | ||
| + | * What is the function Q( A, B, C ) implemented by the circuit shown to the right, where the gates are NAND gates (an AND gate combined with a NOT gate on its output)? | ||
| + | * What is the diagram of Q using only NOT, OR, and AND gates? | ||
| + | * What is the '''minterm canonical form''' of Q? | ||
Latest revision as of 07:03, 29 January 2009
(c) --D. Thiebaut 22:01, 28 January 2009 (UTC)
Back to Main Page
This assignment is due on Wednesday evening, at the beginning of Lab 2.
Problem 1
Assume that we define a Boolean Algebra where the two values possible are { α, β }, and where the operators are U, T, and NOT.
The U operator has the following truth table:
| x | y | x U y |
|---|---|---|
|
α |
α |
α |
|
α |
β |
α |
|
β |
α |
α |
|
β |
β |
β |
The T operator has the following truth table:
| x | y | x T y |
|---|---|---|
|
α |
α |
α |
|
α |
β |
β |
|
β |
α |
β |
|
β |
β |
β |
Which of these assertions is true?
- α is 1, β is 0, U is the AND operator, and T the OR operator
- α is 0, β is 1, U is the OR operator, and T is the AND operator
Be sure to explain why one assertion is true, or why it is false!
Problem 2
Expand and simplify the function defined as f(a, b, c, d ) = Σ(0, 1, 2, 8, 10, 12, 13, 14, 15)
Expand and simplify the function defined as g(a, b, c, d ) = Σ( 3, 4, 5, 6, 7, 9, 11 )
Make sure you use your head and think!!!
Problem 3
- What is the function Q( A, B, C ) implemented by the circuit shown to the right, where the gates are NAND gates (an AND gate combined with a NOT gate on its output)?
- What is the diagram of Q using only NOT, OR, and AND gates?
- What is the minterm canonical form of Q?