Difference between revisions of "CSC270 Homework 3"
(→Exercise 2) |
(→Exercise 2) |
||
| Line 24: | Line 24: | ||
What is the simplified expression of the function g(a, b, c, d, e) expressed by the Karnaugh map above? | What is the simplified expression of the function g(a, b, c, d, e) expressed by the Karnaugh map above? | ||
| + | |||
| + | =Exercise 3= | ||
| + | |||
| + | Draw the logic diagram for the functions h() and k() below with 4-to-1 multiplexers: | ||
| + | |||
| + | * h( a, b, c, d ) = Σ( 0, 1, 2, 3, 4, 6, 12, 14 ) | ||
| + | |||
| + | * k( a, b, c ) = &Sigma( 0, 1, 2, 3, 7 ) | ||
| + | |||
| + | Draw the logic diagram of the same functions with 8-to-1 multiplexers. | ||
| + | |||
| + | |||
| + | =Exercise 4= | ||
| + | |||
| + | Implement a 16-to-1 multiplexer with only 4-to-1 multiplexers. | ||
Revision as of 14:06, 11 February 2009
© D. Thiebaut, 2009
Back to Weekly Schedule
This assignment is due on Wednesday evening, at the beginning of Lab 4.
Contents
Exercise 1
Assume that we have a boolean function f(a, b, c, d) = Σ( 5, 7, 15 ).
- What is its minimal form, as given by a Karnaugh map?
Assume furthermore we know that the the signals a and b are never both equal to 1 at the same time, and that c and d are never both equal to 00 at the same time. So, for example, the signals a, b, c, d will never be in the state 1 1 0 1, because that would require a, and b to be 1. Similarly, the condition a = 0, b=1, c=0, d=0 will never occur either, because c and d are 0 in this case.
How can we use this information to our advantage, as logic designers?
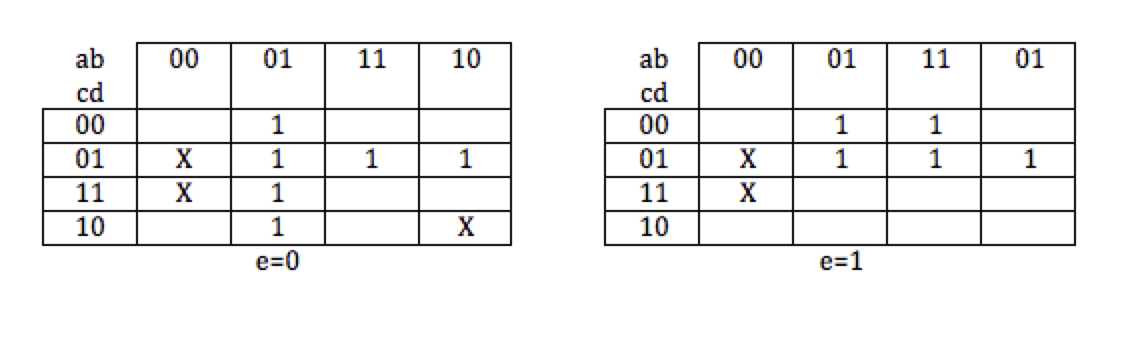
Exercise 2
What is the simplified expression of the function g(a, b, c, d, e) expressed by the Karnaugh map above?
Exercise 3
Draw the logic diagram for the functions h() and k() below with 4-to-1 multiplexers:
- h( a, b, c, d ) = Σ( 0, 1, 2, 3, 4, 6, 12, 14 )
- k( a, b, c ) = &Sigma( 0, 1, 2, 3, 7 )
Draw the logic diagram of the same functions with 8-to-1 multiplexers.
Exercise 4
Implement a 16-to-1 multiplexer with only 4-to-1 multiplexers.