Difference between revisions of "XGrid Tutorial Part 1: Monte Carlo"
(→Starting several instances of montecarlo.py) |
(→First, the serial version of the program) |
||
| (48 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
| width="60%" | __TOC__ | | width="60%" | __TOC__ | ||
| <bluebox> | | <bluebox> | ||
| − | This tutorial is intended for running distributed programs on an | + | This tutorial is intended for running distributed programs on an 8-core MacPro that is setup as an XGrid Controller at Smith College. Most of the steps presented here should work on other Apple grids, except for the specific details of login and host addresses. |
| + | |||
| + | Another document details how to access the 88-processor XGrid in the Science Center at Smith College. | ||
This document supersedes and extends the original tutorial [[CSC334_Introduction_to_the_XGrid_at_Smith_College |CSC334 Introduction to the XGrid at Smith College]]. | This document supersedes and extends the original tutorial [[CSC334_Introduction_to_the_XGrid_at_Smith_College |CSC334 Introduction to the XGrid at Smith College]]. | ||
| Line 8: | Line 10: | ||
|} | |} | ||
| + | This is one of several tutorials on the XGrid at Smith College. | ||
| + | * [[XGrid Tutorial Part 1: Monte Carlo | Part I]]: Monte Carlo | ||
| + | * [[XGrid Tutorial Part 2: Processing Wikipedia Pages | Part II]]: Processing Wikipedia Pages | ||
| + | * [[XGrid Tutorial Part 3: Monte Carlo on the Science Center XGrid | Part III]]: Monte Carlo on Smith's 88-core XGrid. | ||
| + | |||
=Setup= | =Setup= | ||
<tanbox> | <tanbox> | ||
This section assumes that you are using your own computer, or a computer in a lab, and that you have a '''secure shell client''' available on your computer. You will use the secure shell to connect to a host in the XGrid and run your programs from there. | This section assumes that you are using your own computer, or a computer in a lab, and that you have a '''secure shell client''' available on your computer. You will use the secure shell to connect to a host in the XGrid and run your programs from there. | ||
</tanbox> | </tanbox> | ||
| + | |||
| Line 27: | Line 35: | ||
==Important Concepts== | ==Important Concepts== | ||
| − | * '''job''': typically a program or collection of programs, along with their data files submitted to | + | * '''job''': typically a program or collection of programs, along with their data files submitted to an Apple XGrid. |
* '''tasks''': a division of a job into smaller pieces containing a program or programs with its/their data file(s). | * '''tasks''': a division of a job into smaller pieces containing a program or programs with its/their data file(s). | ||
<br /> | <br /> | ||
| Line 42: | Line 50: | ||
* Use one of the Windows, Linux, or Mac computers available to you and open an''' SSH window'''. | * Use one of the Windows, Linux, or Mac computers available to you and open an''' SSH window'''. | ||
| − | * Connect to DT's Mac Pro using your | + | * Connect to DT's Mac Pro using your CSC352 account. |
<onlysmith> | <onlysmith> | ||
| − | '''ssh -Y 352b- | + | '''ssh -Y 352b-xx@xgridmac.dyndns.org''' |
</onlysmith> | </onlysmith> | ||
| − | * When prompted for a '''password''', use the one given | + | * When prompted for a '''password''', use the one given to you. |
* Create a '''.bash_profile''' file in your account on the MacPro for simplifying the connection to the Grid (you will need to do this only once, the first time you connect to the Mac Pro): | * Create a '''.bash_profile''' file in your account on the MacPro for simplifying the connection to the Grid (you will need to do this only once, the first time you connect to the Mac Pro): | ||
| Line 69: | Line 77: | ||
</onlysmith> | </onlysmith> | ||
| − | * Make sure you replace the string '''xxx_xxx_xxx_xxx''' with the one that will be given to you. | + | * Make sure you replace the string '''xxx_xxx_xxx_xxx''' with the one that will be given to you. This password is not the one associated with the 352b-xx account. It is a password to access the XGrid. |
| − | * | + | * Save the file. |
* Make the operating system read this file as if you had just logged in: | * Make the operating system read this file as if you had just logged in: | ||
| Line 94: | Line 102: | ||
:You are discovering the format used by Apple to code information. It is similar to XML, but uses braces. It is called the PLIST format. We'll see it again later, when we deal with batch jobs. | :You are discovering the format used by Apple to code information. It is similar to XML, but uses braces. It is called the PLIST format. We'll see it again later, when we deal with batch jobs. | ||
| + | |||
| + | <greenbox> | ||
| + | [[Image:ComputerLogo.png|right |100px]] | ||
| + | ;Lab Experiment #1: | ||
| + | :Perform all the steps above to verify that you can connect to the XGrid. | ||
| + | </greenbox> | ||
=Your First Distributed Program: Monte Carlo= | =Your First Distributed Program: Monte Carlo= | ||
<tanbox> | <tanbox> | ||
| − | In this section you will learn how to run a Python program on the XGrid in '''synchronous''' and '''asynchronous''' modes. | + | In this section you will learn how to run a Python program on the XGrid in '''synchronous''' and '''asynchronous''' modes. The synchronous is only used for information. The asynchronous approach will be our preferred method. |
</tanbox> | </tanbox> | ||
==First, the serial version of the program== | ==First, the serial version of the program== | ||
[[Image:montecarloPi.gif | 200px | right]] | [[Image:montecarloPi.gif | 200px | right]] | ||
| − | We'll pick something simple to start with: a monte-carlo Python program that generates an approximation of Pi. You can find some good information on the monte-carlo method [http:// | + | We'll pick something simple to start with: a monte-carlo Python program that generates an approximation of Pi. You can find some good information on the monte-carlo method [http://www.cs.nyu.edu/courses/fall06/G22.2112-001/MonteCarlo.pdf here]. A good flash demonstration is available [http://www.hellam.net/piday/carlo.html here] as well. |
The Python code is shown below. | The Python code is shown below. | ||
<source lang="python"> | <source lang="python"> | ||
| + | . | ||
| + | |||
#!/usr/bin/env python | #!/usr/bin/env python | ||
# montecarlo.py | # montecarlo.py | ||
| Line 138: | Line 154: | ||
# print approximation of pi | # print approximation of pi | ||
print 30 * '-' | print 30 * '-' | ||
| − | print | + | print N, ":", 4.0 * count_inside / count |
| + | |||
| + | . | ||
</source> | </source> | ||
| Line 158: | Line 176: | ||
sys 0m0.010s | sys 0m0.010s | ||
| − | * To test several | + | * To test several numbers of samples, we can use a Bash for-loop, as follows (This command can be entered directly at the prompt): |
| Line 198: | Line 216: | ||
</pre></code> | </pre></code> | ||
| − | You see that even with ten million samples, we do not get a very accurate value of Pi (3.14147) and it still | + | You see that even with ten million samples, we do not get a very accurate value of Pi (3.14147) and it still takes 12 seconds of user time. |
===Running the program on 1 Processor, on the XGrid=== | ===Running the program on 1 Processor, on the XGrid=== | ||
| Line 204: | Line 222: | ||
Although we feel that our program contains some parallelism, with all the samples being generated independently of each other, this parallelism cannot be exploited directly by the XGrid. The XGrid only deals with '''tasks''', which are individual programs. The XGrid won't really be able to run our program any differently than the way we have done so far. But at least we can submit the program to the XGrid and get familiar with the process. | Although we feel that our program contains some parallelism, with all the samples being generated independently of each other, this parallelism cannot be exploited directly by the XGrid. The XGrid only deals with '''tasks''', which are individual programs. The XGrid won't really be able to run our program any differently than the way we have done so far. But at least we can submit the program to the XGrid and get familiar with the process. | ||
| − | The XGrid supports two modes of operation: '''synchronous''' and '''asynchronous'''. In '''synchronous''' mode, you send the XGrid your program, | + | The XGrid supports two modes of operation: '''synchronous''' and '''asynchronous'''. |
| + | |||
| + | In '''synchronous''' mode, you send the XGrid server your program, the XGrid server runs it, and then when the program is finished, the XGrid server returns the results back to you. | ||
In the '''asynchronous''' mode, however, you submit your program as a job, and you can continue issuing more Linux commands. Every so often you poll the XGrid to see if the job is done, and if it is, you ask the XGrid for the results generated by your job. | In the '''asynchronous''' mode, however, you submit your program as a job, and you can continue issuing more Linux commands. Every so often you poll the XGrid to see if the job is done, and if it is, you ask the XGrid for the results generated by your job. | ||
| Line 211: | Line 231: | ||
Let's ask the XGrid to run our program: | Let's ask the XGrid to run our program: | ||
| − | xgrid - job run ''montecarlo.py 100000'' | + | xgrid - job '''run''' ''montecarlo.py 100000'' |
Note that the result comes back to the screen. The synchronous submission is fine for running the program once. One reason is that the xgrid command is blocked and won't let us access the prompt until the application has finished. Unfortunately, if we want to launch several different tasks at the same time, this will not be helpful. Instead, the '''asynchronous''' submission will let us do just that. | Note that the result comes back to the screen. The synchronous submission is fine for running the program once. One reason is that the xgrid command is blocked and won't let us access the prompt until the application has finished. Unfortunately, if we want to launch several different tasks at the same time, this will not be helpful. Instead, the '''asynchronous''' submission will let us do just that. | ||
| Line 226: | Line 246: | ||
} | } | ||
| − | Basically the XGrid system | + | Basically the XGrid system behaves as the daily counter your local grocery store: it gives us a ticket with a number on it. We can go do our shopping, and when we're ready we return back to the counter, present our ticket, and if the job is done, we get your results back. |
| − | + | To see if the job is finished, we use the integer specified in the '''jobIdentifier''' line and poll the server: | |
'''xgrid -id''' ''ddddd'' '''-job attributes''' | '''xgrid -id''' ''ddddd'' '''-job attributes''' | ||
| − | + | We get back something like this: | |
| − | |||
| − | |||
{ | { | ||
| Line 270: | Line 288: | ||
Whenever you submit a job asynchronously (the most frequent case), follow these simple rules: | Whenever you submit a job asynchronously (the most frequent case), follow these simple rules: | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
{| style="width:100%" border="1" | {| style="width:100%" border="1" | ||
|- | |- | ||
| Line 285: | Line 306: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | |||
| + | <greenbox> | ||
| + | [[Image:ComputerLogo.png|100px|right]] | ||
| + | ;Lab Experiment 2 | ||
| + | :Create your own version of the Monte-Carlo program and submit it asynchronously, retrieve the results, and delete it. | ||
| + | </greenbox> | ||
====Asynchronous Submission to the XGrid with style!==== | ====Asynchronous Submission to the XGrid with style!==== | ||
| Line 290: | Line 317: | ||
Computer scientists do not like to type commands at the keyboard if they can write a script that will perform the same task. And rightly so. | Computer scientists do not like to type commands at the keyboard if they can write a script that will perform the same task. And rightly so. | ||
| − | We are going to use a script to submit asynchronous jobs. The script will grab the output of the xgrid command when we submit the job, get the jobIdentifier from | + | We are going to use a script to submit asynchronous jobs. |
| + | |||
| + | The script will | ||
| + | # grab the output of the xgrid command when we submit the job, | ||
| + | # get the jobIdentifier from the output and | ||
| + | # keep on polling the grid for the status of the job, until the job has finished. | ||
| + | # When the job has finished, the script will ask for the results back. | ||
| + | # Finally the script will remove the job from the grid. | ||
A (crude and not terribly robust) version of this script is available [[CSC352 getXGridOutput.py | here]]. | A (crude and not terribly robust) version of this script is available [[CSC352 getXGridOutput.py | here]]. | ||
| Line 300: | Line 334: | ||
chmod +x getXGridOutput.py | chmod +x getXGridOutput.py | ||
| − | * Submit the job and pipe it through the | + | * Submit the job and pipe it through the script: |
xgrid -job submit montecarlo.py 100000 | getXGridOutput.py | xgrid -job submit montecarlo.py 100000 | getXGridOutput.py | ||
| Line 309: | Line 343: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | <greenbox> | ||
| + | [[Image:ComputerLogo.png|100px|right]] | ||
| + | ;Lab Experiment #3: | ||
| + | : Create your own version of [[CSC352 getXGridOutput.py |getXGridOutput.py]], make it executable, and use it to get the output of the XGrid job submission of '''montecarlo.py'''. | ||
| + | |||
| + | </greenbox> | ||
==Finally, Some Parallelism== | ==Finally, Some Parallelism== | ||
| Line 316: | Line 356: | ||
Ok, time to put all this together and figure out a way to generate an approximation of Pi with a large number of samples utilizing as much parallelism as possible, or as much parallelism as required to reach the shortest execution time. | Ok, time to put all this together and figure out a way to generate an approximation of Pi with a large number of samples utilizing as much parallelism as possible, or as much parallelism as required to reach the shortest execution time. | ||
| − | Think of the problem at hand: we want to generate a huge number of samples | + | Think of the problem at hand: we want to generate a huge number of samples, but in parallel, gather the number of points falling inside the different circles, and in the different squares, and figure out how we can combine the results together to get our approximation of Pi. |
| − | + | Do you see a simple solution? | |
| − | An obvious one is to discover that if we have two different experiments, one counting the number of inside samples as ''ni_1'' and the total number of samples as ''N'', and the other experiments counting them as ''ni_2'' and ''N'', then we can get a better estimate as 4 * (''ni_1'' + ''ni_2'' ) / ( ''N'' + ''N'' ) = 4 * ( ''ni_1''/(2''N'') + ''ni_2''/(2''N'') ) = ( ''Pi_1'' + ''Pi_2'' )/2, where ''Pi_1'' and ''Pi_2'' are the approximations computed in the two experiments. | + | An obvious one is to discover that if we have two different experiments, one counting the number of inside samples as ''ni_1'' and the total number of samples as ''N'', and the other experiments counting them as ''ni_2'' and ''N'', then we can combine these numbers and get a better estimate of Pi as 4 * (''ni_1'' + ''ni_2'' ) / ( ''N'' + ''N'' ) = 4 * ( ''ni_1''/(2''N'') + ''ni_2''/(2''N'') ) = ( ''Pi_1'' + ''Pi_2'' )/2, where ''Pi_1'' and ''Pi_2'' are the approximations computed in the two experiments. |
<center> | <center> | ||
| Line 337: | Line 377: | ||
<br /> | <br /> | ||
So, all we need is to get the different approximations generated by different '''montecarlo.py''' experiments and average them out, and we'll get a better approximation, hopefully. | So, all we need is to get the different approximations generated by different '''montecarlo.py''' experiments and average them out, and we'll get a better approximation, hopefully. | ||
| − | |||
===Starting several instances of montecarlo.py=== | ===Starting several instances of montecarlo.py=== | ||
| Line 343: | Line 382: | ||
Here's how we can start several (in this case 4) copies of the program and run them in parallel on the XGrid: | Here's how we can start several (in this case 4) copies of the program and run them in parallel on the XGrid: | ||
| − | for i in {1..4}; do '''xgrid -job submit montecarlo.py 100000'''; done | getXGridOutput.py | + | for i in {1..4}; do '''xgrid -job submit montecarlo.py 100000'''; done | ./getXGridOutput.py |
The for-loop is taken from the examples appearing in http://www.cyberciti.biz/faq/bash-for-loop/ | The for-loop is taken from the examples appearing in http://www.cyberciti.biz/faq/bash-for-loop/ | ||
| − | The output of the execution of the 4 commands '''xgrid -job submit montecarlo.py 100000''' is ''piped'' through the getXGridOutput.py program which is clever enough | + | The output of the execution of the 4 commands '''xgrid -job submit montecarlo.py 100000''' is ''piped'' through the getXGridOutput.py program which is clever enough to discover that there are 4 tasks running, and which will gather the 4 individual outputs and will delete the 4 tasks from the server when they're done. |
The output will be something like this: | The output will be something like this: | ||
| Line 370: | Line 409: | ||
Total execution time: 0.000000 seconds | Total execution time: 0.000000 seconds | ||
| − | + | <font color="red">Note that we have modified the output of '''montecarlo.py''' so that it displays '''N''' and '''pi''' on two separate lines. </font> | |
| + | |||
| + | <br /> | ||
| − | Below is a simple attempt at performing this task. The fully documented version is available [[CSC352 gatherResultsMonteCarlo.py | here]]: | + | All we have to do now is either store this output to a file, then read it, gather the values of pi, and average them out, or better, pipe this output to '''another Python program''' that will read and parse these lines, gather the values of pi, and output the average. |
| + | |||
| + | Below is a simple attempt at performing this task. The fully documented version of this new program is available [[CSC352 gatherResultsMonteCarlo.py | here]]: | ||
<source lang="python"> | <source lang="python"> | ||
#! /usr/bin/env python | #! /usr/bin/env python | ||
| + | # gatherResults.py | ||
import sys | import sys | ||
| Line 402: | Line 446: | ||
</source> | </source> | ||
| − | = | + | We use it as follows: |
| − | + | ||
| − | + | for i in {1..4}; do xgrid -job submit montecarlo.py 100000; done | ./getXGridOutput.py | ./gatherResults.py | |
| − | + | ||
| − | + | The output looks as follows: | |
| − | == | + | |
| − | + | Job 1315 stopped: Execution time: 0.000000 seconds | |
| + | ------------------------------ | ||
| + | N= 100000 | ||
| + | pi= 3.138 | ||
| + | Job 1316 stopped: Execution time: 0.000000 seconds | ||
| + | ------------------------------ | ||
| + | N= 100000 | ||
| + | pi= 3.14744 | ||
| + | Job 1317 stopped: Execution time: 1.000000 seconds | ||
| + | ------------------------------ | ||
| + | N= 100000 | ||
| + | pi= 3.1412 | ||
| + | Job 1314 stopped: Execution time: 0.000000 seconds | ||
| + | ------------------------------ | ||
| + | N= 100000 | ||
| + | pi= 3.13408 | ||
| + | |||
| + | Total execution time: 1.000000 seconds | ||
| + | |||
| + | |||
| + | <font color="magenta">Average pi = 3.14018 | ||
| + | Total Execution time = 1.0</font> | ||
| − | + | <greenbox> | |
| − | + | [[Image:ComputerLogo.png|100px|right]] | |
| + | ;Lab Experiment #4 | ||
| + | : Create the new Python script in your directory, and practice running '''montecarlo.py''' on several XGrid ''agents''. Make sure you can keep an eye on the XGrid GUI Monitoring tool as you submit jobs. | ||
| + | </greenbox> | ||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | =Lab Summary= | ||
| + | {| | ||
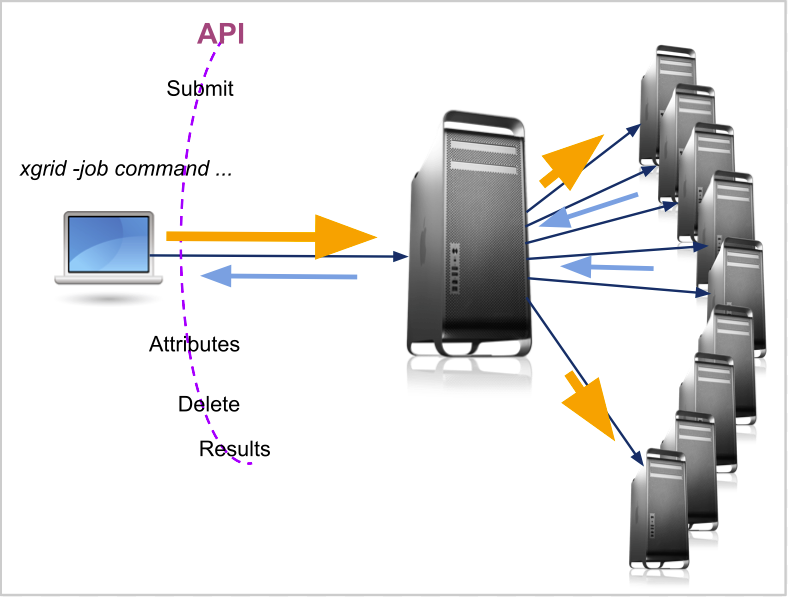
| + | |[[Image:XGridAPI.png | 500px]] | ||
| + | | | ||
| + | * xgrid provides an API | ||
| + | ** submit | ||
| + | ** attributes | ||
| + | ** results | ||
| + | ** delete | ||
| + | * xgrid command runs locally | ||
| + | * xgrid controller out of our control | ||
| + | |- | ||
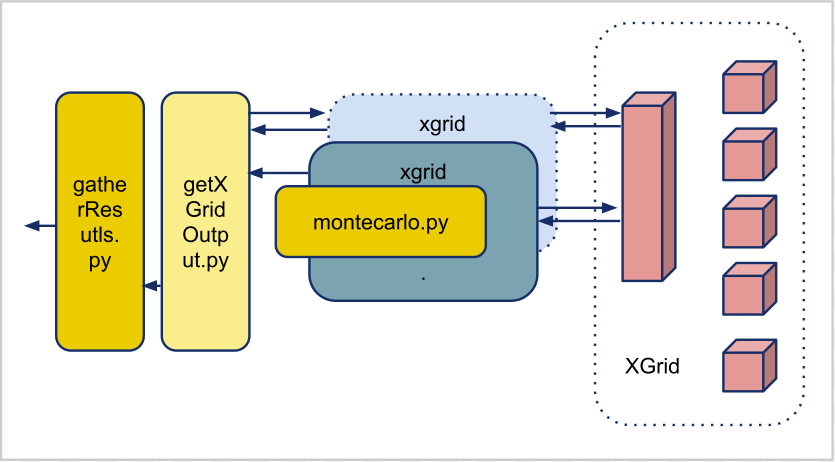
| + | | [[Image:XGrid_Piping.png | 500px]]</center> | ||
| + | | | ||
| + | * montecarlo.py sandwiched and packaged | ||
| + | * piping gathers and coalesces the results | ||
| + | ** getXGridOUtput polls and gets outputs. Independent of application. | ||
| + | ** gatherResults gets outputs and generates final estimates of Pi. Is extension of montecarlo program. | ||
| + | |} | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | |||
| − | |||
| − | + | <greenbox> | |
| − | + | [[Image:ComputerLogo.png|100px|right]] | |
| − | + | ;Lab Experiment 5 | |
| − | + | :The following [[CSC352 StrangeShape.py | Python program]] contains a class representing a ''strange'' shape contained in the unit square (1x1). You can quiz an object generated from this class and ask if a given Point (x, y) is inside or outside the shape. Your problem: find an XGrid solution for figuring out the area of the shape... | |
| − | + | :Work in a group! | |
| + | </greenbox> | ||
| + | |||
| + | =For Mac Users...= | ||
| + | |||
| + | If you have a Mac and Want to Monitor your Distributed Programs you may find this [[XGrid on a Mac| page]] of interest! | ||
| + | |||
| + | =Continue on to Lab 2= | ||
| + | |||
| + | Lab 2 deals with pipelines of commands and processing Wikipedia pages: [[XGrid Tutorial Part 2: Processing Wikipedia Pages | Lab 2]] | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Line 437: | Line 527: | ||
<br /> | <br /> | ||
| − | [[Category:XGrid]][[Category:CSC352]][[Category:Tutorials]] | + | [[Category:XGrid]][[Category:CSC352]][[Category:Tutorials]][[Category:Python]] |
Latest revision as of 09:37, 5 December 2016
| This tutorial is intended for running distributed programs on an 8-core MacPro that is setup as an XGrid Controller at Smith College. Most of the steps presented here should work on other Apple grids, except for the specific details of login and host addresses. Another document details how to access the 88-processor XGrid in the Science Center at Smith College. This document supersedes and extends the original tutorial CSC334 Introduction to the XGrid at Smith College. |
This is one of several tutorials on the XGrid at Smith College.
- Part I: Monte Carlo
- Part II: Processing Wikipedia Pages
- Part III: Monte Carlo on Smith's 88-core XGrid.
Setup
This section assumes that you are using your own computer, or a computer in a lab, and that you have a secure shell client available on your computer. You will use the secure shell to connect to a host in the XGrid and run your programs from there.
XGrid General Setup
(taken from http://www.macresearch.org/the_xgrid_tutorials_part_i_xgrid_basics)
Important Concepts
- job: typically a program or collection of programs, along with their data files submitted to an Apple XGrid.
- tasks: a division of a job into smaller pieces containing a program or programs with its/their data file(s).
- controller: the main computer in the XGrid in charge of distributing work to the agents
- agent: the other computers in the XGrid
- client: the user or computer where the user sits, where jobs are issued.
Connection, Bash Profile, Test
The XGrid system is available for the Mac platform only. In order to use it, you will have to connect to a Mac Pro that is a client and also the server of a grid (named XGrid).
- Use one of the Windows, Linux, or Mac computers available to you and open an SSH window.
- Connect to DT's Mac Pro using your CSC352 account.
- When prompted for a password, use the one given to you.
- Create a .bash_profile file in your account on the MacPro for simplifying the connection to the Grid (you will need to do this only once, the first time you connect to the Mac Pro):
emacs -nw .bash_profile
- Copy/paste the text below in it.
export EDITOR=/usr/bin/emacs export TERM=xterm-color export PATH=$PATH:. #export PS1="\w> " PS1='[\h]\n[\t] \w\$: ' PS2='> '# setup xgrid access
- Make sure you replace the string xxx_xxx_xxx_xxx with the one that will be given to you. This password is not the one associated with the 352b-xx account. It is a password to access the XGrid.
- Save the file.
- Make the operating system read this file as if you had just logged in:
source .bash_profile
- (Another way would have been to logout and login again.)
- Check that the XGrid is up and that you can connect to it:
xgrid -grid attributes -gid 0
- the output should be similar to what is shown below:
{
gridAttributes = {
gridMegahertz = 0;
isDefault = YES;
name = Xgrid;
};
}
- You are discovering the format used by Apple to code information. It is similar to XML, but uses braces. It is called the PLIST format. We'll see it again later, when we deal with batch jobs.
 |  | |
| ||
 |  |
Your First Distributed Program: Monte Carlo
In this section you will learn how to run a Python program on the XGrid in synchronous and asynchronous modes. The synchronous is only used for information. The asynchronous approach will be our preferred method.
First, the serial version of the program
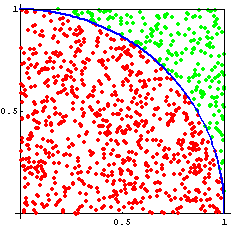
We'll pick something simple to start with: a monte-carlo Python program that generates an approximation of Pi. You can find some good information on the monte-carlo method here. A good flash demonstration is available here as well.
The Python code is shown below.
.
#!/usr/bin/env python
# montecarlo.py
# taken from http://www.eveandersson.com/pi/monte-carlo-circle
# Usage:
# python montecarlo.py N
# or
# ./montecarlo N
#
# where N is the number of samples wanted.
# the approximation of pi is printed after the samples have been
# generated.
#
import random
import math
import sys
# get the number of samples from the command line
# or assign 1E6 as the default number of samples.
N = 1000000
if len( sys.argv ) > 1:
N = int( sys.argv[1] )
# generate the samples and keep track of counts
count_inside = 0
for count in range( N ):
d = math.hypot(random.random(), random.random())
if d < 1: count_inside += 1
count += 1
# print approximation of pi
print 30 * '-'
print N, ":", 4.0 * count_inside / count
.
Running the serial program
- Store the program in a file called montecarlo.py, and make it executable as follows:
chmod +x montecarlo.py
- Run the program and measure its execution time for 1000 samples:
time ./montecarlo.py 1000 ------------------------------ 1000 : 3.136 real 0m0.026s user 0m0.016s sys 0m0.010s
- To test several numbers of samples, we can use a Bash for-loop, as follows (This command can be entered directly at the prompt):
for N in 1000 10000 100000 1000000 10000000; do time ./montecarlo.py $N; done
- Here's the output:
------------------------------
1000 : 3.136
real 0m0.026s
user 0m0.016s
sys 0m0.010s
------------------------------
10000 : 3.1592
real 0m0.035s
user 0m0.026s
sys 0m0.009s
------------------------------
100000 : 3.14472
real 0m0.141s
user 0m0.130s
sys 0m0.011s
------------------------------
1000000 : 3.14366
real 0m1.208s
user 0m1.183s
sys 0m0.023s
------------------------------
10000000 : 3.1414768
real 0m11.901s
user 0m11.732s
sys 0m0.162s
You see that even with ten million samples, we do not get a very accurate value of Pi (3.14147) and it still takes 12 seconds of user time.
Running the program on 1 Processor, on the XGrid
Although we feel that our program contains some parallelism, with all the samples being generated independently of each other, this parallelism cannot be exploited directly by the XGrid. The XGrid only deals with tasks, which are individual programs. The XGrid won't really be able to run our program any differently than the way we have done so far. But at least we can submit the program to the XGrid and get familiar with the process.
The XGrid supports two modes of operation: synchronous and asynchronous.
In synchronous mode, you send the XGrid server your program, the XGrid server runs it, and then when the program is finished, the XGrid server returns the results back to you.
In the asynchronous mode, however, you submit your program as a job, and you can continue issuing more Linux commands. Every so often you poll the XGrid to see if the job is done, and if it is, you ask the XGrid for the results generated by your job.
Synchronous Submission
Let's ask the XGrid to run our program:
xgrid - job run montecarlo.py 100000
Note that the result comes back to the screen. The synchronous submission is fine for running the program once. One reason is that the xgrid command is blocked and won't let us access the prompt until the application has finished. Unfortunately, if we want to launch several different tasks at the same time, this will not be helpful. Instead, the asynchronous submission will let us do just that.
Asynchronous Submission
Let's do the same thing, i.e. submit the program to the XGrid, and run it on one processor, but asynchronously.
xgrid -job submit montecarlo.py 100000
You will not get the results of your program. Instead you get something like this:
{
jobIdentifier = ddddd;
}
Basically the XGrid system behaves as the daily counter your local grocery store: it gives us a ticket with a number on it. We can go do our shopping, and when we're ready we return back to the counter, present our ticket, and if the job is done, we get your results back.
To see if the job is finished, we use the integer specified in the jobIdentifier line and poll the server:
xgrid -id ddddd -job attributes
We get back something like this:
{
jobAttributes = {
activeCPUPower = 0;
applicationIdentifier = "com.apple.xgrid.cli";
dateNow = 2010-02-15 18:04:17 -0500;
dateStarted = 2010-02-15 18:03:59 -0500;
dateStopped = 2010-02-15 18:04:00 -0500;
dateSubmitted = 2010-02-15 18:03:59 -0500;
jobStatus = Finished;
name = "montecarlo.py";
percentDone = 100;
taskCount = 1;
undoneTaskCount = 0;
};
}
When we see that the jobStatus is Finished, we can ask for the results back:
xgrid -id ddddd -job results ------------------------------ 1000000 : 3.139436
Finally, we should clean up the XGrid and remove our job, as the XGrid will keep it in memory otherwise:
xgrid -id ddddd -job delete
{
}
Asynchronous Submission Rules
Whenever you submit a job asynchronously (the most frequent case), follow these simple rules:
|
 |  | |
| ||
 |  |
Asynchronous Submission to the XGrid with style!
Computer scientists do not like to type commands at the keyboard if they can write a script that will perform the same task. And rightly so.
We are going to use a script to submit asynchronous jobs.
The script will
- grab the output of the xgrid command when we submit the job,
- get the jobIdentifier from the output and
- keep on polling the grid for the status of the job, until the job has finished.
- When the job has finished, the script will ask for the results back.
- Finally the script will remove the job from the grid.
A (crude and not terribly robust) version of this script is available here.
- Use emacs and copy/paste to create your own copy of it.
- Make it executable
chmod +x getXGridOutput.py
- Submit the job and pipe it through the script:
xgrid -job submit montecarlo.py 100000 | getXGridOutput.py
- Verify that you get the result from montecarlo.py.
 |  | |
| ||
 |  |
Finally, Some Parallelism
Let's think about it...
Ok, time to put all this together and figure out a way to generate an approximation of Pi with a large number of samples utilizing as much parallelism as possible, or as much parallelism as required to reach the shortest execution time.
Think of the problem at hand: we want to generate a huge number of samples, but in parallel, gather the number of points falling inside the different circles, and in the different squares, and figure out how we can combine the results together to get our approximation of Pi.
Do you see a simple solution?
An obvious one is to discover that if we have two different experiments, one counting the number of inside samples as ni_1 and the total number of samples as N, and the other experiments counting them as ni_2 and N, then we can combine these numbers and get a better estimate of Pi as 4 * (ni_1 + ni_2 ) / ( N + N ) = 4 * ( ni_1/(2N) + ni_2/(2N) ) = ( Pi_1 + Pi_2 )/2, where Pi_1 and Pi_2 are the approximations computed in the two experiments.
|
Pi ~ 4 * (ni_1)/(N) |
Pi ~ 4 * (ni_2)/(N) |
So, all we need is to get the different approximations generated by different montecarlo.py experiments and average them out, and we'll get a better approximation, hopefully.
Starting several instances of montecarlo.py
Here's how we can start several (in this case 4) copies of the program and run them in parallel on the XGrid:
for i in {1..4}; do xgrid -job submit montecarlo.py 100000; done | ./getXGridOutput.py
The for-loop is taken from the examples appearing in http://www.cyberciti.biz/faq/bash-for-loop/
The output of the execution of the 4 commands xgrid -job submit montecarlo.py 100000 is piped through the getXGridOutput.py program which is clever enough to discover that there are 4 tasks running, and which will gather the 4 individual outputs and will delete the 4 tasks from the server when they're done.
The output will be something like this:
Job 1083 stopped: Execution time: 0.000000 seconds ------------------------------ N= 100000 pi= 3.14432 Job 1084 stopped: Execution time: 0.000000 seconds ------------------------------ N= 100000 pi= 3.14052 Job 1085 stopped: Execution time: 0.000000 seconds ------------------------------ N= 100000 pi= 3.14216 Job 1082 stopped: Execution time: 0.000000 seconds ------------------------------ N= 100000 pi= 3.1398 Total execution time: 0.000000 seconds
Note that we have modified the output of montecarlo.py so that it displays N and pi on two separate lines.
All we have to do now is either store this output to a file, then read it, gather the values of pi, and average them out, or better, pipe this output to another Python program that will read and parse these lines, gather the values of pi, and output the average.
Below is a simple attempt at performing this task. The fully documented version of this new program is available here:
#! /usr/bin/env python
# gatherResults.py
import sys
pis = []
# get the lines generated by getXGridOutput.py
for line in sys.stdin:
print line, # print line for user to see
# look for pi
if line.find( "pi=" ) != -1:
pi = float( line.split( '=' )[-1] )
pis.append( pi )
continue
# get total execution time
if line.find( "Total execution" )!= -1:
totalExec = float( line.split( )[3] )
# we're done reading the output. Pring summary
print "Average pi = ", sum( pis )/len( pis )
print "Total Execution time = ", totalExec
We use it as follows:
for i in {1..4}; do xgrid -job submit montecarlo.py 100000; done | ./getXGridOutput.py | ./gatherResults.py
The output looks as follows:
Job 1315 stopped: Execution time: 0.000000 seconds ------------------------------ N= 100000 pi= 3.138 Job 1316 stopped: Execution time: 0.000000 seconds ------------------------------ N= 100000 pi= 3.14744 Job 1317 stopped: Execution time: 1.000000 seconds ------------------------------ N= 100000 pi= 3.1412 Job 1314 stopped: Execution time: 0.000000 seconds ------------------------------ N= 100000 pi= 3.13408 Total execution time: 1.000000 seconds Average pi = 3.14018 Total Execution time = 1.0
 |  | |
| ||
 |  |
Lab Summary
 |  | |
| ||
 |  |
For Mac Users...
If you have a Mac and Want to Monitor your Distributed Programs you may find this page of interest!
Continue on to Lab 2
Lab 2 deals with pipelines of commands and processing Wikipedia pages: Lab 2