CSC270 Lab 3 2012

--D. Thiebaut 15:09, 14 February 2012 (EST)

---

This lab deals with decoders, and in particular the 74LS42, and will have you look at using the decoder as a building block of combinational circuits, or as a dedicated decoder.

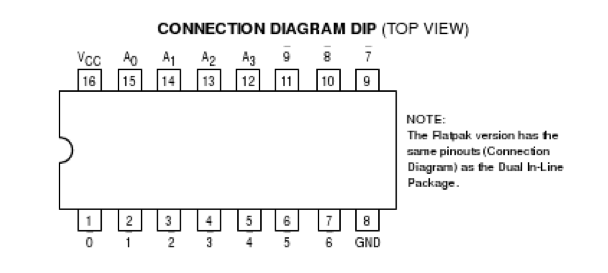
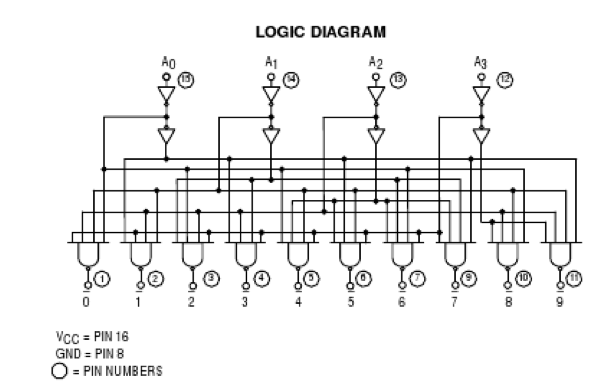
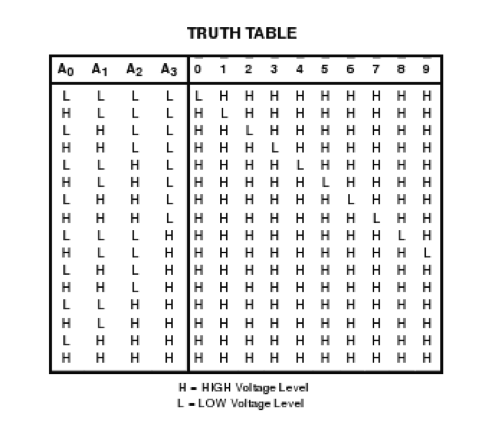
The 74LS42 Datasheet

Experiment #1

Study the 74LS42 data-sheet. Observe it carefully and figure out what kind of decoder it is:

Question 1

Is it a 3-to-8 decoder? A 4-to-16 decoder? If not, then what?

Question 2

Does it have an enable input signal?

Question 3

Are the outputs active high or active low?

Using the schematics as your guide, design a 3-to-8 decoder with enable and active-low outputs using the 74LS42 as your main circuit. The challenge here is that you only have 4 LEDs to show outputs. You cannot use one LED connected to two different outputs, or one of the outputs will get damaged in the process. You'll have to switch back and forth between LEDs and signals to show one set of outputs, for example the lower 4 output bits, and the other set of outputs, i.e. the upper 4 output bits.

Experiment #2: Challenge of the day

Use a 74LS42 to implement one of two different circuits, depending on your mood:

• a majority voter of 3 input signals.
• a two-bit binary adder

Use as few extra circuits (not gates, circuits) as possible, in addition to the 74LS42!

Experiment #3

We should have seen in class the basic concept of a multiplexer. (Wikipedia has a nice description of a multiplexer.)

Pick a simple design for a multiplexer, implement it (use Karnaugh maps!), and demonstrate that it works.