Difference between revisions of "CSC111 Lab 13 2014"
(→First Modification) |
(→Binary Search) |
||
| (15 intermediate revisions by the same user not shown) | |||
| Line 111: | Line 111: | ||
:*Explain the pattern made by the printed lines. Why this shape? | :*Explain the pattern made by the printed lines. Why this shape? | ||
:*Where does the stopping condition appear in the printed lines? In other words, where is the printed statement that indicates that '''fact()''' just received a value of ''n'' equal to 1? Why isn't this statement at the end of the printout? | :*Where does the stopping condition appear in the printed lines? In other words, where is the printed statement that indicates that '''fact()''' just received a value of ''n'' equal to 1? Why isn't this statement at the end of the printout? | ||
| + | <br /> | ||
| + | =Thinking Recursively= | ||
| + | <br /> | ||
| + | All the challenges below require you to put together a recursive function for a simple problem. | ||
| + | |||
| + | Thinking recursively is extremely challenging and takes a while to master! So don't despair. | ||
| + | |||
| + | Here is a simple set of points to remember when building a recursive function: | ||
| + | <br /> | ||
| + | <tanbox> | ||
| + | :# First figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's should expect to receive back from a call to itself.<br /><br /> | ||
| + | :# What is the '''stopping condition'''? What is the smallest problem you can solve without recursion? That's the first thing you want to test for and do in your recursive function.<br /><br /> | ||
| + | :# If the stopping condition doesn't apply, and the function has to do some work, figure out how to make one or several recursive calls to the function, get some intermediate results back, combine them together and get the final answer. That's the '''recursive step'''.<br /> | ||
| + | </tanbox> | ||
| + | <br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Line 122: | Line 137: | ||
<br /> | <br /> | ||
| − | * Given a number ''n'', compute recursively the sum of all the numbers from 1 to ''n''. For example, if you pass ''n'' = 5 to the solution function, it will return 5+4+3+2+1 | + | * Given a number ''n'', compute recursively the sum of all the numbers from 1 to ''n''. For example, if you pass ''n'' = 5 to the solution function, it will return 15 (which is equal to 5+4+3+2+1) |
<br /> | <br /> | ||
<br /> | <br /> | ||
| Line 160: | Line 175: | ||
* Write a recursive function that returns the largest element of a list L using the following formula: | * Write a recursive function that returns the largest element of a list L using the following formula: | ||
<br /> | <br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | {| width="100%" | ||
| + | | style="width: 20%; text-align:right;" | | ||
| + | ''largest''( L ) | ||
| + | | style="width: 40%;" | | ||
| + | = L[0] | ||
| + | | style="width: 40%;" | | ||
| + | if len( L ) == 1 | ||
| + | |- | ||
| + | | | ||
| + | | ||
| + | | | ||
| + | = max( L[0], largest( L[1:] ) ) | ||
| + | | | ||
| + | otherwise. We assume N=len(L) | ||
| + | |} | ||
:Test your program on different Arrays of varying sizes. We assume that the arrays will always have at least one element. | :Test your program on different Arrays of varying sizes. We assume that the arrays will always have at least one element. | ||
| Line 190: | Line 213: | ||
| style="width: 20%; text-align:right;" | | | style="width: 20%; text-align:right;" | | ||
''largest''( L ) | ''largest''( L ) | ||
| − | | style="width: | + | | style="width: 40%;" | |
| − | = | + | = L[0] |
| − | | style="width: | + | | style="width: 40%;" | |
if len( L ) == 1 | if len( L ) == 1 | ||
|- | |- | ||
| Line 251: | Line 274: | ||
<br /> | <br /> | ||
| + | <!-- | ||
{| style="width:100%; background:silver" | {| style="width:100%; background:silver" | ||
|- | |- | ||
| Line 265: | Line 289: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | + | --> | |
<br /> | <br /> | ||
<br /> | <br /> | ||
| Line 271: | Line 295: | ||
<br /> | <br /> | ||
| + | <!-- | ||
=Binary Search= | =Binary Search= | ||
<br /> | <br /> | ||
| Line 298: | Line 323: | ||
* Run your program and pick keys that are either listed in the array of 10 consecutive array items, or pick keys that are in between some of the 10 numbers (i.e. not in the list). Observe how few steps are required to see if the keys are in the list or not. | * Run your program and pick keys that are either listed in the array of 10 consecutive array items, or pick keys that are in between some of the 10 numbers (i.e. not in the list). Observe how few steps are required to see if the keys are in the list or not. | ||
| − | * Make your List of size 1,000,000. Predict how many recursive steps are required to find whether a kew is in the list or not. Verify if your intuition is correct or not. | + | * Make your List of size 1,000,000. Predict how many recursive steps are required to find whether a kew is in the list or not. Verify if your intuition is correct or not. '''Note: your program will spend a few seconds at the beginning creating and sorting the array. Be patient!''' |
| − | + | * Is the number of steps required to find a number always the same? Could it be possible to find a number in the list with just one probe? See if you can make it happen and demonstrate your solution to me! | |
<br /> | <br /> | ||
| + | --> | ||
<!-- | <!-- | ||
==Optional and for fun: Exploring a Maze== | ==Optional and for fun: Exploring a Maze== | ||
| Line 352: | Line 378: | ||
--> | --> | ||
<br /> | <br /> | ||
| + | |||
| + | <br /> | ||
| + | |||
| + | =Fractal Trees= | ||
| + | [[File:FractalTree.png|right|250px]] | ||
| + | <br /> | ||
| + | This is just something for you to play with. You do not have to include this into your '''lab13.py''' program. Just create a new program with the code you'll find on [[CSC111_FractalTree.py| this page]], put it in the same directory where you store your '''graphics111.py''' directory. You may want to call your program '''fractalTree.py'''. | ||
| + | |||
| + | The program generates a ''fractal'' tree. Fractals are self-similar objects: they look the same on a small scale as they do on a larger scale. | ||
| + | |||
| + | * Run the program first | ||
| + | * Then look at the code and see if you can figure out how the recursion works. | ||
| + | * To see how the different parameters influence the drawing of the ''fractal tree'', modify the following parameters, one at a time, and give them different values: | ||
| + | |||
| + | ; theta | ||
| + | : in the main program, change the angle '''theta''' which controls how much a branch will diverge from the direction of the branch that supports it. Try 0.4 first. Then try values between 0 and 0.8. | ||
| + | |||
| + | ; level of recursion | ||
| + | : the main program passes '''9''' to the function as a starting level of recursion. Try passing smaller numbers first, then larger numbers (but less than 13 or so). | ||
| + | |||
| + | ; trunk_ratio | ||
| + | : recursive function defines this as 0.29 and that represents the length of the trunk relative to its two branches. Try ratios between 0.1 (10%) and 0.9 (90%). | ||
| + | |||
| + | <br /> | ||
| + | |||
=Submission= | =Submission= | ||
<br /> | <br /> | ||
| − | Submit the program ''' | + | Submit the program '''lab13.py''' to this URL: [http://cs.smith.edu/~thiebaut/111b/submitL13.php http://cs.smith.edu/~thiebaut/111b/submitL13.php]. |
| + | |||
| + | <br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | <!-- | ||
| + | =Solution Program= | ||
<br /> | <br /> | ||
| + | <source lang="python"> | ||
| + | # solution programs for Lab13 | ||
| + | # | ||
| + | # | ||
| + | from random import randrange | ||
| + | |||
| + | def fact( n ): | ||
| + | print( "fact function started. Received n =", n ) | ||
| + | print( "testing if %d is >= 1" % (n) ) | ||
| + | |||
| + | if n<=1: | ||
| + | print( "n == 1. Returning 1" ) | ||
| + | return 1 | ||
| + | |||
| + | print( "n > 1. Calling fact( %d )" % (n-1) ) | ||
| + | y = fact( n-1 ) | ||
| + | print( "setting y to %d" % y ) | ||
| + | result = n * y | ||
| + | print( "returning result = %d * %d = %d" % (n, y, n*y) ) | ||
| + | return result | ||
| + | |||
| + | def fact2( n, indent ): | ||
| + | print( indent, "fact2(%d) started" % n ) | ||
| + | print( indent, "comparing %d to 1" % n ) | ||
| + | if n<=1: | ||
| + | print( indent, "%d is <= 1. Returning 1" % 1 ) | ||
| + | return 1 | ||
| + | |||
| + | print( indent, "%d is not <= 1. Calling fact2(%d) and storing it in y" % (n, n-1) ) | ||
| + | y = fact2( n-1, indent + " " ) | ||
| + | print( indent, "just received %d from fact2( %d )." % ( y, n-1 ) ) | ||
| + | result = n * y | ||
| + | print( indent, "multiplied %d by %d. It's %d. Returning %d to caller" % ( n, y, result, result ) ) | ||
| + | return result | ||
| + | |||
| + | def sum1( n ): | ||
| + | if n==1: | ||
| + | return 1 | ||
| + | return n + sum1( n-1 ) | ||
| + | |||
| + | def evenSum1( n ): | ||
| + | if n <= 1: | ||
| + | return 0 | ||
| + | |||
| + | if n%2 == 0: | ||
| + | return n + evenSum1( n-2 ) | ||
| + | if n%2 == 1: | ||
| + | return evenSum1( n-1 ) | ||
| + | |||
| + | def recurseMax( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | return L[0] | ||
| + | |||
| + | return max( L[0], recurseMax( L[1:] ) ) | ||
| + | |||
| + | def divideConquerLargest( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | return L[0] | ||
| + | |||
| + | return max( divideConquerLargest( L[0:N//2] ), | ||
| + | divideConquerLargest( L[N//2: ] ) ) | ||
| + | |||
| + | def divideConquerMin( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | return L[0] | ||
| + | |||
| + | return min( divideConquerMin( L[0:N//2] ), | ||
| + | divideConquerMin( L[N//2: ] ) ) | ||
| + | |||
| + | |||
| + | def divideConquerSum( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | return L[0] | ||
| + | |||
| + | return divideConquerSum( L[0:N//2] ) + divideConquerSum( L[N//2: ] ) | ||
| + | |||
| + | |||
| + | def divideConquerAbs( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | L[0] = abs( L[0] ) | ||
| + | return L | ||
| + | |||
| + | return divideConquerAbs( L[0:N//2] ) + divideConquerAbs( L[N//2: ] ) | ||
| + | |||
| + | |||
| + | #------------------------------------------------------------------ | ||
| + | def createArray( n ): | ||
| + | """Creates a list of n random numbers in sorted order""" | ||
| + | A= [] | ||
| + | for i in range( n ): | ||
| + | A.append( randrange( n * 10 ) ) | ||
| + | |||
| + | A.sort() | ||
| + | return A | ||
| + | |||
| + | #------------------------------------------------------------------ | ||
| + | def binsearch( A, low, high, key ): | ||
| + | """a recursive function that searches the list A to see if | ||
| + | it contains the item key between the indexes "low" and "high". | ||
| + | returns the index where the key was found, or -1 otherwise | ||
| + | """ | ||
| + | |||
| + | print( "low=%10d high=%10d key=%10d" % (low, high, key) ) | ||
| + | |||
| + | if low>high: | ||
| + | return -1 | ||
| + | |||
| + | mid = ( low + high )//2 | ||
| + | if A[mid]==key: | ||
| + | return mid | ||
| + | |||
| + | if key < A[mid]: | ||
| + | return binsearch( A, low, mid-1, key ) | ||
| + | else: | ||
| + | return binsearch( A, mid+1, high, key ) | ||
| + | |||
| + | |||
| + | |||
| + | def main(): | ||
| + | # fact | ||
| + | """ | ||
| + | n = int( input( "Enter a positive number: " ) ) | ||
| + | x = fact( n ) | ||
| + | print( "the factorial of %d is %d." % ( n , x ) ) | ||
| + | """ | ||
| + | |||
| + | # fact2 | ||
| + | """ | ||
| + | n = int( input( "Enter a positive number: " ) ) | ||
| + | x = fact2( n, " " ) | ||
| + | print( "the factorial of %d is %d." % ( n , x ) ) | ||
| + | """ | ||
| + | |||
| + | # sum1 | ||
| + | """ | ||
| + | n = int( input( "Enter a positive number: " ) ) | ||
| + | print( "sum of all numbers from 1 to %d = %d" % (n, sum1(n) ) ) | ||
| + | """ | ||
| + | |||
| + | # evenSum1 | ||
| + | """ | ||
| + | for n in range( 12 ): | ||
| + | print( " n = %d sumEven(%d) returns %d" % (n, n, evenSum1(n) ) ) | ||
| + | """ | ||
| + | |||
| + | # recursive max | ||
| + | """ | ||
| + | L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] | ||
| + | print( "recurseMax( %s ) = %d" % ( L, recurseMax( L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # divideConquerLargest | ||
| + | """ | ||
| + | L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] | ||
| + | print( "divideConquerLargest( %s ) = %d" % (L, divideConquerLargest(L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # divideConquerMin | ||
| + | """ | ||
| + | L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] | ||
| + | print( "divideConquerMin( %s ) = %d" % (L, divideConquerMin(L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # divideConquerSum | ||
| + | """ | ||
| + | L = [1, 2, 3, 10, 101, 100, 100] | ||
| + | print( "divideConquerSum( %s ) = %d" % (L, divideConquerSum(L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # divideConquerAbs | ||
| + | """ | ||
| + | L = [1, 2, 3, -10, -101, 100, 100] | ||
| + | print( "divideConquerAbs( %s ) = %s" % (L, divideConquerAbs(L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # binSearch | ||
| + | #A = createArray( 20 ) | ||
| + | #print( "A = ", A ) | ||
| + | |||
| + | A = createArray( 1000000 ) | ||
| + | print( A[100:110] ) | ||
| + | |||
| + | while True: | ||
| + | print | ||
| + | key = int( input( "search for what number? " ) ) | ||
| + | if key==-1: break | ||
| + | index = binsearch( A, 0, len( A )-1, key ) | ||
| + | if index != -1: | ||
| + | print( "found %d at index %d" % ( key, index ) ) | ||
| + | else: | ||
| + | print( "%d not in A" % key ) | ||
| + | main() | ||
| + | |||
| + | </source> | ||
| + | --> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
[[Category:CSC111]][[Category:Python]][[Category:Labs]] | [[Category:CSC111]][[Category:Python]][[Category:Labs]] | ||
Latest revision as of 16:22, 30 April 2014
--D. Thiebaut (talk) 19:43, 28 April 2014 (EDT)
|
This lab deals with recursive functions, and solving problems recursively. |
Program Name
- Call your program lab13.py
Visualizing Recursive Factorial At Work
Create a copy of this simple example:
# factorial.py
# Demonstrates a recursive factorial function
def fact( n ):
if n<=1:
return 1
y = fact( n-1 )
result = n * y
return result
def main():
n = int( input( "Enter a positive number: " ) )
x = fact( n )
print( "the factorial of %d is %d." % ( n , x ) )
main()
- Run your program
- It will prompt you for a number and will return its factorial.
- Verify that it computes the correct result. Below are some factorials numbers to compare your output to.
1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 6! = 720 7! = 5040 8! = 40320 9! = 362880 10! = 3628800 11! = 39916800 12! = 479001600 13! = 6227020800 14! = 87178291200
Visualizing, Step 1
- Add print statements to your fact() function so that it will let you know exactly what it does. For example, before it tests to see if n is less than equal to 1, you could print:
print( "fact function started. Receives n =", n )
print( "testing if %d is >= 1" % (n) )
- Add print statements that will show the values of y and result.
- Run your program and observe its output. Can you see better how the function fact() recursively calls itself?
Visualizing, Step 2
- Create the more sophisticated program shown below. Observe it well first, and try to figure out what the indent variable does.
# factorialPrint.py # Demonstrates a recursive factorial function def fact2( n, indent ): print( indent, "fact2(%d) started" % n ) print( indent, "comparing %d to 1" % n ) if n<=1: print( indent, "%d is <= 1. Returning 1" % 1 ) return 1 print( indent, "%d is not <= 1. Calling fact2(%d) and storing it in y" % (n, n-1) ) y = fact2( n-1, indent + " " ) print( indent, "just received %d from fact2( %d )." % ( y, n-1 ) ) result = n * y print( indent, "multiplied %d by %d. It's %d. Returning %d to caller" % ( n, y, result, result ) ) return result def main(): n = input( "Enter a positive integer: " ) print( "Main calls fact( %d )" % n ) y = fact2( n, " " ) print( "Main receives result = ", y ) main()
- Run the program
- Explain the pattern made by the printed lines. Why this shape?
- Where does the stopping condition appear in the printed lines? In other words, where is the printed statement that indicates that fact() just received a value of n equal to 1? Why isn't this statement at the end of the printout?
Thinking Recursively
All the challenges below require you to put together a recursive function for a simple problem.
Thinking recursively is extremely challenging and takes a while to master! So don't despair.
Here is a simple set of points to remember when building a recursive function:
- First figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's should expect to receive back from a call to itself.
- What is the stopping condition? What is the smallest problem you can solve without recursion? That's the first thing you want to test for and do in your recursive function.
- If the stopping condition doesn't apply, and the function has to do some work, figure out how to make one or several recursive calls to the function, get some intermediate results back, combine them together and get the final answer. That's the recursive step.
- First figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's should expect to receive back from a call to itself.
Challenge 1: Recursive Sum |
- Given a number n, compute recursively the sum of all the numbers from 1 to n. For example, if you pass n = 5 to the solution function, it will return 15 (which is equal to 5+4+3+2+1)
Challenge 2: Recursive Even Sum |
- Given a number n, compute recursively the sum of all the even and positive numbers less than or equal to n.
- This is trickier than it seems! Here is an example of running a loop and asking the recursive function to compute the sum of all the even numbers up to n when n ranges from 0 to 12.
n = 0 sumEven(0) returns 0 n = 1 sumEven(1) returns 0 n = 2 sumEven(2) returns 2 n = 3 sumEven(3) returns 2 n = 4 sumEven(4) returns 6 n = 5 sumEven(5) returns 6 n = 6 sumEven(6) returns 12 n = 7 sumEven(7) returns 12 n = 8 sumEven(8) returns 20 n = 9 sumEven(9) returns 20 n = 10 sumEven(10) returns 30 n = 11 sumEven(11) returns 30
Challenge 3: Recursive Max |
- Write a recursive function that returns the largest element of a list L using the following formula:
|
largest( L ) |
= L[0] |
if len( L ) == 1 |
|
|
= max( L[0], largest( L[1:] ) ) |
otherwise. We assume N=len(L) |
- Test your program on different Arrays of varying sizes. We assume that the arrays will always have at least one element.
- Hints
- the function definition is simply def largest( L ):
- write the stopping condition first (if len(L)...)
- if the stopping condition is not met, compute the max() of L[0] and largest( L minus the first element )
def largest( A ):
if len( A )==1:
return A[0]
return max( A[0], largest( A[1:] ) )
Divide and Conquer Recursion
- We now take a slightly different approach. This time we take a list, divide it two halves, recursively process the two halves, and combine the result of the results obtained on both sides.
- As an example, assume we have to find the largest item in a list L. Here's a possible way to describe the recursive divide-and-conquer approach:
|
largest( L ) |
= L[0] |
if len( L ) == 1 |
|
|
= max( largest( L[0:N/2], largest( L[N/2:] ) ) |
otherwise. We assume N=len(L) |
The code equivalent to this definition is shown below:
def divideConquerLargest( L ): N = len( L ) if N==1: return L[0] return max( divideConquerLargest( L[0:N//2] ), divideConquerLargest( L[N//2: ] ) )
- Run this code, and verify that it returns the largest element of an unsorted list of integers.
L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] print( "divideConquerLargest( %s ) = %d" % (L, divideConquerLargest(L ) ) )
Challenge 4: Divide-and-Conquer Min |
- Write a recursive function that uses the divide and conquer approach to find the smallest element in a list L.
Challenge 5: Divide-and-Conquer Sum |
- Write a recursive function that uses the divide and conquer approach to compute the sum of all the elements in a list L.
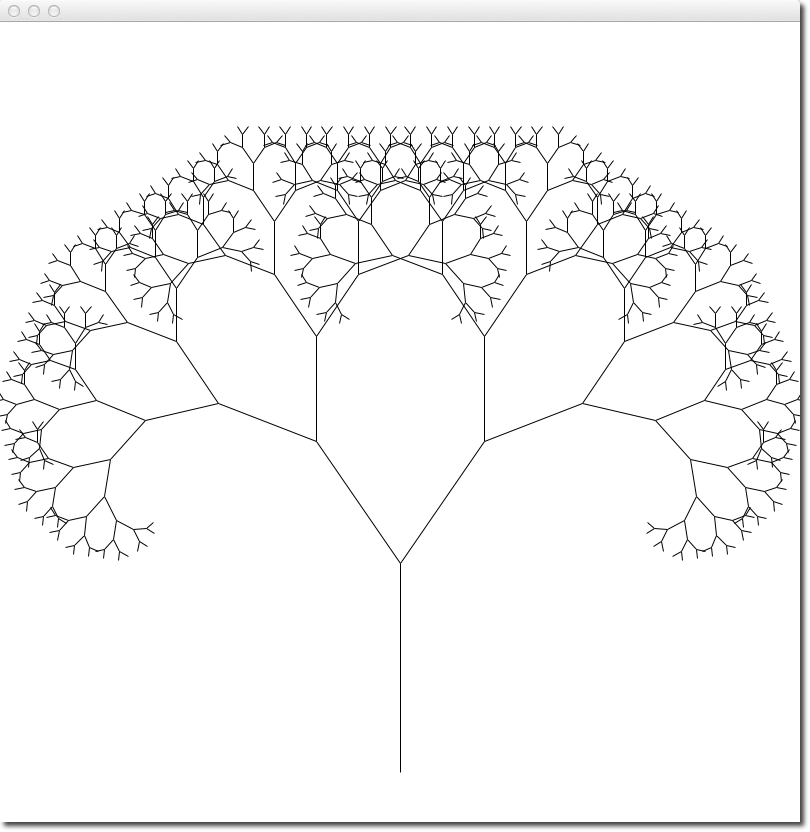
Fractal Trees
This is just something for you to play with. You do not have to include this into your lab13.py program. Just create a new program with the code you'll find on this page, put it in the same directory where you store your graphics111.py directory. You may want to call your program fractalTree.py.
The program generates a fractal tree. Fractals are self-similar objects: they look the same on a small scale as they do on a larger scale.
- Run the program first
- Then look at the code and see if you can figure out how the recursion works.
- To see how the different parameters influence the drawing of the fractal tree, modify the following parameters, one at a time, and give them different values:
- theta
- in the main program, change the angle theta which controls how much a branch will diverge from the direction of the branch that supports it. Try 0.4 first. Then try values between 0 and 0.8.
- level of recursion
- the main program passes 9 to the function as a starting level of recursion. Try passing smaller numbers first, then larger numbers (but less than 13 or so).
- trunk_ratio
- recursive function defines this as 0.29 and that represents the length of the trunk relative to its two branches. Try ratios between 0.1 (10%) and 0.9 (90%).
Submission
Submit the program lab13.py to this URL: http://cs.smith.edu/~thiebaut/111b/submitL13.php.