Difference between revisions of "CSC111 FractalTree.py"
| (3 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
<br /> | <br /> | ||
<source lang="python"> | <source lang="python"> | ||
| − | # | + | # fractalTree.py |
# D. Thiebaut | # D. Thiebaut | ||
# Code taken from http://openbookproject.net/thinkcs/python/english3e/recursion.html | # Code taken from http://openbookproject.net/thinkcs/python/english3e/recursion.html | ||
| Line 75: | Line 75: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | =Some Fractal Trees from the Web= | ||
<br /> | <br /> | ||
| + | <center>[[Image:fractalTree1.jpg|500px]]</center> | ||
| + | <br /><center>From [http://ictisocs.blogspot.com/2010_10_01_archive.html http://ictisocs.blogspot.com/2010_10_01_archive.html]</center> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | ==Toy Story. Watch the trees in the chase scene!== | ||
| + | <br /> | ||
| + | <center><videoflash>dIsFg3FSpEQ</videoflash></center> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
Latest revision as of 11:33, 29 April 2014
--D. Thiebaut (talk) 07:45, 29 April 2014 (EDT)
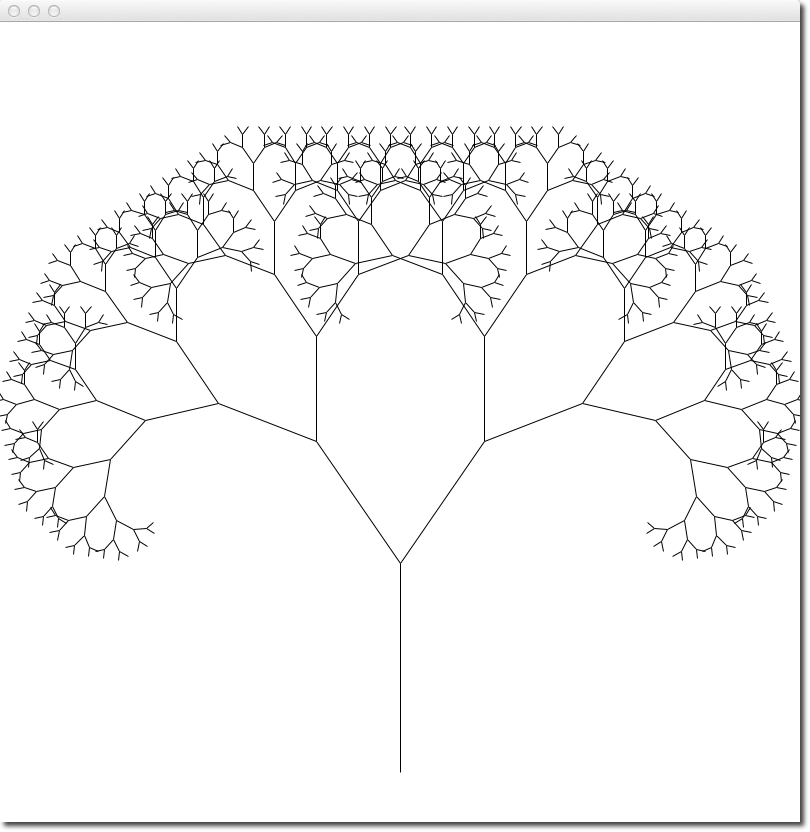
Fractal Tree
# fractalTree.py
# D. Thiebaut
# Code taken from http://openbookproject.net/thinkcs/python/english3e/recursion.html
# and adapted to work with graphics111.py.
#
# Draws a fractal tree on the graphic window.
#
from graphics111 import *
import math
import time
import random
# dimensions of the window
MAXWIDTH = 800
MAXHEIGHT = 800
# recursive tree-drawing function
#
def draw_tree(canvas, # the canvas
order, # the level of recursion. Starts positive.
theta, # angle of new branch leaving this trunk
sz, # size of this branch
x, y, # coordinates of base of this branch
heading # angle of direction of this branch
):
trunk_ratio = 0.29 # How big is the trunk relative to whole tree?
trunk = sz * trunk_ratio # length of trunk
# compute x, y of end of the current branch
delta_x = trunk * math.cos(heading)
delta_y = trunk * math.sin(heading)
x2, y2 = x + delta_x, y + delta_y
# draw current branch
canvas.setFill( 0,0,0 )
canvas.drawLine(x, y, x2, y2)
# if this branch has sub-branches, then recurse
if order > 0:
# make the recursive calls to draw the two subtrees
newsz = sz*(1 - trunk_ratio)
draw_tree(canvas,
order-1, theta, newsz, x2, y2, heading-theta )
draw_tree(canvas,
order-1, theta, newsz, x2, y2, heading+theta )
# draw 1 tree in the middle of the screen, shooting straight up.
def main():
win = GraphicsWindow(MAXWIDTH, MAXHEIGHT)
canvas = win.canvas()
theta = 0.01 # use 0.02 for tall skinny trees, 0.7 for fat trees
draw_tree(canvas,
9,
theta,
MAXWIDTH*0.9, MAXWIDTH//2,
MAXHEIGHT-50,
-math.pi/2)
win.wait()
win.close()
main()
Some Fractal Trees from the Web

Toy Story. Watch the trees in the chase scene!