Difference between revisions of "CSC111 Lab 12 2015"
(→Optional and for fun: Exploring a Maze) |
|||
| (15 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
<bluebox> | <bluebox> | ||
This lab deals with recursive functions. Programming recursive functions is a challenging concept to master. The best way to proceed is to write many different recursive solutions and observe the behavior of the functions as they perform their work. Eventually recursion will start making sense. It is normal to not fully understand it at first. Keep at it. Little by little, it will become natural thinking. | This lab deals with recursive functions. Programming recursive functions is a challenging concept to master. The best way to proceed is to write many different recursive solutions and observe the behavior of the functions as they perform their work. Eventually recursion will start making sense. It is normal to not fully understand it at first. Keep at it. Little by little, it will become natural thinking. | ||
| + | <br /> | ||
| + | Feel free to work in ''pair-programming'' mode for this lab. There is nothing to submit on Moodle this week, but do not skip another opportunity to program and practice Python to get ready for the final exam! | ||
</bluebox> | </bluebox> | ||
|} | |} | ||
<br /> | <br /> | ||
| − | = | + | |
| + | |||
| + | |||
| + | <showafterdate after="20150422 12:00" before="20150601 00:00"> | ||
<br /> | <br /> | ||
| + | =Visualizing Recursive Factorial At Work= | ||
| + | <br /> | ||
| + | |||
Create a copy of this simple example: | Create a copy of this simple example: | ||
| − | + | ||
| − | <source lang="python"> | + | ::<source lang="python"> |
| − | # | + | # factorial.py |
| − | # | + | # Demonstrates a recursive factorial function |
| − | |||
def fact( n ): | def fact( n ): | ||
| + | # stopping condition | ||
if n<=1: | if n<=1: | ||
return 1 | return 1 | ||
| + | # recursive step | ||
y = fact( n-1 ) | y = fact( n-1 ) | ||
result = n * y | result = n * y | ||
| Line 31: | Line 40: | ||
n = int( input( "Enter a positive number: " ) ) | n = int( input( "Enter a positive number: " ) ) | ||
x = fact( n ) | x = fact( n ) | ||
| − | print( "the factorial of" | + | print( "the factorial of %d is %d." % ( n , x ) ) |
main() | main() | ||
| − | |||
</source> | </source> | ||
| Line 56: | Line 64: | ||
13! = 6227020800 | 13! = 6227020800 | ||
14! = 87178291200 | 14! = 87178291200 | ||
| + | <br /> | ||
| + | ==Visualizing, Step 1== | ||
| + | <br /> | ||
| + | :*Add print statements to your '''fact()''' function so that it will let you know exactly what it does. For example, before it tests to see if ''n'' is less than equal to 1, you could print: | ||
| − | + | <br /> | |
| − | + | <source lang="python"> | |
| − | + | print( "fact function started. Receives n =", n ) | |
| − | + | print( "testing if %d is >= 1" % (n) ) | |
| − | print("fact function started. Receives n =", n ) | + | </source> |
| − | print( "testing if | + | <br /> |
| − | |||
:*Add print statements that will show the values of '''y''' and '''result'''. | :*Add print statements that will show the values of '''y''' and '''result'''. | ||
| − | :*Run your program and observe its output. | + | :*Run your program and observe its output. Can you see better how the function ''fact()'' recursively calls itself? |
<br /> | <br /> | ||
| − | = | + | ==Visualizing, Step 2== |
<br /> | <br /> | ||
| − | * Create the more sophisticated program shown below. Observe it well first, and try to figure out what the '''indent''' variable does. | + | :*Create the more sophisticated program shown below. Observe it well first, and try to figure out what the '''indent''' variable does. |
<br /> | <br /> | ||
::<source lang="python"> | ::<source lang="python"> | ||
# factorialPrint.py | # factorialPrint.py | ||
| − | # Demonstrates a recursive factorial function | + | # Demonstrates a recursive factorial function |
| − | + | ||
| − | def | + | def fact2( n, indent ): |
| − | print( indent, " | + | print( indent, "fact2(%d) started" % n ) |
| − | print( indent, "comparing | + | print( indent, "comparing %d to 1" % n ) |
if n<=1: | if n<=1: | ||
| − | print( indent | + | print( indent, "%d is <= 1. Returning 1" % 1 ) |
return 1 | return 1 | ||
| − | print( indent | + | print( indent, "%d is not <= 1. Calling fact2(%d) and storing it in y" % (n, n-1) ) |
| − | + | y = fact2( n-1, indent + " " ) | |
| − | y = | + | print( indent, "just received %d from fact2( %d )." % ( y, n-1 ) ) |
| − | |||
| − | print( indent, "just received" | ||
result = n * y | result = n * y | ||
| − | print( indent, "multiplied" | + | print( indent, "multiplied %d by %d. It's %d. Returning %d to caller" % ( n, y, result, result ) ) |
return result | return result | ||
def main(): | def main(): | ||
| − | |||
n = int( input( "Enter a positive integer: " ) ) | n = int( input( "Enter a positive integer: " ) ) | ||
| − | print( "Main calls fact(" | + | print( "Main calls fact( %d )" % n ) |
| − | + | y = fact2( n, " " ) | |
| − | y = | + | print( "Main receives result = ", y ) |
| − | |||
| − | print( "Main receives result | ||
main() | main() | ||
| − | + | ||
</source> | </source> | ||
| − | *Run the program | + | :*Run the program |
| − | *Explain the pattern made by the printed lines. Why this shape? | + | :*Explain the pattern made by the printed lines. Why this shape? |
| − | *Where does the stopping condition appear in the printed lines? In other words, where is the printed statement that indicates that '''fact()''' just received a value of ''n'' equal to 1? Why isn't this statement at the end of the printout? | + | :*Where does the stopping condition appear in the printed lines? In other words, where is the printed statement that indicates that '''fact()''' just received a value of ''n'' equal to 1? Why isn't this statement at the end of the printout? |
| + | <br /> | ||
| + | =Thinking Recursively= | ||
| + | <br /> | ||
| + | All the challenges below require you to put together a recursive function for a simple problem. | ||
| + | |||
| + | Thinking recursively is quite challenging and takes a while to master. So don't despair! | ||
| + | Here are points to remember when building a recursive function: | ||
| + | <br /> | ||
| + | <tanbox> | ||
| + | :# First, figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's what it should expect to receive back from a call to itself.<br /><br /> | ||
| + | :# What is the '''stopping condition'''? What is the smallest problem you can solve without recursion? That's the first thing you want to test for and do in your recursive function.<br /><br /> | ||
| + | :# If the stopping condition doesn't apply, and the function has to do some work, figure out how to make one or several recursive calls to the function, get some intermediate results back, combine them together and get the final answer. That's the '''recursive step'''.<br /> | ||
| + | </tanbox> | ||
<br /> | <br /> | ||
| − | |||
<br /> | <br /> | ||
| − | |||
| − | |||
<br /> | <br /> | ||
| + | {| style="width:100%; background:silver" | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==Challenge 1: Recursive Sum== | ||
| + | |} | ||
| + | [[Image:QuestionMark1.jpg|right|120px]] | ||
<br /> | <br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * Given a number ''n'', compute recursively the sum of all the numbers from 1 to ''n''. For example, if you pass ''n'' = 5 to the solution function, it will return 15 (which is equal to 5+4+3+2+1) | |
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | {| style="width:100%; background:silver" | ||
| + | |- | ||
| + | | | ||
| − | * | + | ==Challenge 2: Recursive Even Sum== |
| + | |} | ||
| + | [[Image:QuestionMark2.jpg|right|120px]] | ||
| + | <br /> | ||
| + | * Given a number ''n'', compute recursively the sum of all the positive '''even''' numbers less than or equal to n. | ||
| + | * This is trickier than it seems! Here is an example of running a loop and asking the recursive function to compute the sum of all the even numbers up to ''n'' when ''n'' ranges from 0 to 12. | ||
| + | <br /> | ||
| + | n = 0 sumEven(0) returns 0 | ||
| + | n = 1 sumEven(1) returns 0 | ||
| + | n = 2 sumEven(2) returns 2 | ||
| + | n = 3 sumEven(3) returns 2 | ||
| + | n = 4 sumEven(4) returns 6 | ||
| + | n = 5 sumEven(5) returns 6 | ||
| + | n = 6 sumEven(6) returns 12 | ||
| + | n = 7 sumEven(7) returns 12 | ||
| + | n = 8 sumEven(8) returns 20 | ||
| + | n = 9 sumEven(9) returns 20 | ||
| + | n = 10 sumEven(10) returns 30 | ||
| + | n = 11 sumEven(11) returns 30 | ||
| + | <br /> | ||
| + | <br /> | ||
| + | {| style="width:100%; background:silver" | ||
| + | |- | ||
| + | | | ||
| + | ==Challenge 3: Recursive Max== | ||
| + | |} | ||
| + | [[Image:QuestionMark3.jpg|right|120px]] | ||
| + | <br /> | ||
| + | * Write a '''recursive function''' that returns the largest element of a list L using the following formula: | ||
| + | <br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | {| width="100%" | ||
| + | | style="width: 20%; text-align:right;" | | ||
| + | ''largest''( L ) | ||
| + | | style="width: 40%;" | | ||
| + | = L[0] | ||
| + | | style="width: 40%;" | | ||
| + | if len( L ) == 1 | ||
| + | |- | ||
| + | | | ||
| + | | ||
| + | | | ||
| + | = max( L[0], largest( L[1:] ) ) | ||
| + | | | ||
| + | otherwise. We assume N=len(L) | ||
| + | |} | ||
| − | + | :Test your program on different lists of varying sizes. We assume that the lists will always have at least one element. | |
| − | |||
| − | |||
| − | |||
| + | : ''' ''Hints'' ''' | ||
| + | :* the function definition is simply '''def largest( L ):''' | ||
| + | :* write the stopping condition first ('''if len(L)...''') | ||
| + | :* if the stopping condition is not met, compute the '''max()''' of '''L[0]''' and '''largest( ''L minus the first element'' )''' | ||
<font color="white"><tt>def largest( A ):<br /> if len( A )==1:<br /> return A[0]<br /> return max( A[0], largest( A[1:] ) ) | <font color="white"><tt>def largest( A ):<br /> if len( A )==1:<br /> return A[0]<br /> return max( A[0], largest( A[1:] ) ) | ||
</tt></font> | </tt></font> | ||
| + | |||
| + | =Divide and Conquer Recursion= | ||
<br /> | <br /> | ||
| − | + | * We now take a slightly different approach. This time we take a list, divide it two halves, recursively process the two halves, and combine the result of the results obtained on both sides. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | * As an example, assume we have to find the largest item in a list '''L'''. Here's a possible way to describe the recursive ''divide-and-conquer'' approach: | ||
<br /> | <br /> | ||
| − | |||
<br /> | <br /> | ||
| − | + | {| width="100%" | |
| − | + | | style="width: 20%; text-align:right;" | | |
| + | ''largest''( L ) | ||
| + | | style="width: 40%;" | | ||
| + | = L[0] | ||
| + | | style="width: 40%;" | | ||
| + | if len( L ) == 1 | ||
| + | |- | ||
| + | | | ||
| + | | ||
| + | | | ||
| + | = max( ''largest''( L[0:N/2], ''largest''( L[N/2:] ) ) | ||
| + | | | ||
| + | otherwise. We assume N=len(L) | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
| − | : | + | The code equivalent to this definition is shown below: |
| − | + | <br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | :<source lang="Python"> | |
| − | + | def divideConquerLargest( L ): | |
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | return L[0] | ||
| + | return max( divideConquerLargest( L[0:N//2] ), | ||
| + | divideConquerLargest( L[N//2: ] ) ) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</source> | </source> | ||
| + | <br /> | ||
| + | * Run this code, and verify that it returns the largest element of an unsorted list of integers. | ||
| + | <br /> | ||
| + | :<source lang="python"> | ||
| + | L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] | ||
| + | print( "divideConquerLargest( %s ) = %d" % (L, divideConquerLargest(L ) ) ) | ||
| + | </source> | ||
| + | <br /> | ||
| + | {| style="width:100%; background:silver" | ||
| + | |- | ||
| + | | | ||
| − | :* | + | ==Challenge 4: Divide-and-Conquer Min== |
| + | |} | ||
| + | [[Image:QuestionMark4.jpg|right|120px]] | ||
| + | <br /> | ||
| + | * Write a recursive function that uses the divide and conquer approach to find the smallest element in a list '''L'''. | ||
| − | : | + | <br /> |
| + | <br /> | ||
| + | {| style="width:100%; background:silver" | ||
| + | |- | ||
| + | | | ||
| − | + | ==Challenge 5: Divide-and-Conquer Sum== | |
| − | : | + | |} |
| − | + | [[Image:QuestionMark6.jpg|right|120px]] | |
| − | + | <br /> | |
| − | + | * Write a recursive function that uses the divide and conquer approach to compute the sum of all the elements in a list '''L'''. | |
| + | <br /> | ||
| + | <br /> | ||
| − | = | + | <!-- |
| − | [[ | + | {| style="width:100%; background:silver" |
| + | |- | ||
| + | | | ||
| + | |||
| + | ==Challenge 6: Divide-and-Conquer Absolute Value== | ||
| + | |} | ||
| + | [[Image:QuestionMark5.jpg|right|120px]] | ||
<br /> | <br /> | ||
| − | + | * Write a recursive function that uses the divide and conquer approach to change all the numbers in a list L to their absolute value. | |
| − | + | :(Hints: the code is much simpler than you think!) | |
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | --> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| − | * Run the program | + | <!-- |
| − | * | + | =Binary Search= |
| − | * | + | <br /> |
| + | * Create a copy of the [[CSC111_BinarySearch.py | binary search program]] we saw in class. | ||
| + | * Read the whole program. Figure out what is going on. | ||
| + | * Run the program and verify that the search function does a good job reporting whether a key entered by the user is in the list or not. | ||
| + | <br /> | ||
| + | ==First Modification== | ||
| + | <br /> | ||
| + | * Modify the recursive function and make it print its parameters (with the exception of A which will be printed in main and does not change). | ||
| + | * Run the program. | ||
| + | * Observe how the binary function quickly reduces the search domain to zoom in the place where the key should be located, if it is in the list. | ||
| + | <br /> | ||
| − | + | ==Second question== | |
| − | + | <br /> | |
| − | + | * Keep the modification you performed in the previous step. | |
| − | + | * Modify the main program as follows | |
| − | + | <br /> | |
| − | + | :<source lang="python"> | |
| − | : | + | A = createArray( 10000 ) |
| + | print( A[100:110] ) | ||
| + | </source> | ||
| + | <br /> | ||
| + | :This way you will have a large array and your program will show a small section of 10 consecutive numbers stored in it. | ||
| + | * Run your program and pick keys that are either listed in the array of 10 consecutive array items, or pick keys that are in between some of the 10 numbers (i.e. not in the list). Observe how few steps are required to see if the keys are in the list or not. | ||
| + | * Make your List of size 1,000,000. Predict how many recursive steps are required to find whether a kew is in the list or not. Verify if your intuition is correct or not. '''Note: your program will spend a few seconds at the beginning creating and sorting the array. Be patient!''' | ||
| + | * Is the number of steps required to find a number always the same? Could it be possible to find a number in the list with just one probe? See if you can make it happen and demonstrate your solution to me! | ||
<br /> | <br /> | ||
| − | = | + | --> |
| + | <!-- | ||
| + | ==Optional and for fun: Exploring a Maze== | ||
<br /> | <br /> | ||
| Line 265: | Line 376: | ||
* Repeat the same experiment as before and change the order in which the recursive function visits the different directions, and observe if this makes the function find the exit faster. | * Repeat the same experiment as before and change the order in which the recursive function visits the different directions, and observe if this makes the function find the exit faster. | ||
| − | == Treasures in the maze== | + | === Treasures in the maze=== |
* Let's change the rules of the game, and make your program find a path to a treasure, rather than a path to an exit. In our case the treasure will be a special character, say '&', inside the maze. | * Let's change the rules of the game, and make your program find a path to a treasure, rather than a path to an exit. In our case the treasure will be a special character, say '&', inside the maze. | ||
* Modify your the visitMaze() function so that it now returns true if it finds the treasure, and not an exit. Verify that your program displays at the end the path to the treasure. | * Modify your the visitMaze() function so that it now returns true if it finds the treasure, and not an exit. Verify that your program displays at the end the path to the treasure. | ||
| + | --> | ||
| + | <br /> | ||
| + | |||
| + | <br /> | ||
| + | |||
| + | =Fractal Trees= | ||
| + | [[File:FractalTree.png|right|250px]] | ||
| + | <br /> | ||
| + | * This exercise is for you to explore recursion in the context of graphics. | ||
| + | |||
| + | * Create a new program with the code you'll find on [[CSC111_FractalTree_2015.py| this page]], put it in the same directory where you store your '''graphics.py''' directory. You may want to call your program '''fractalTree.py'''. | ||
| + | |||
| + | * The program will generate a ''fractal'' tree. Fractals are self-similar objects: they look the same on a small scale as they do on a larger scale. | ||
| + | |||
| + | * Run the program first. | ||
| + | * Look at the code and see if you can figure out how the recursion works. | ||
| + | * To see how the different parameters influence the drawing of the ''fractal tree'', modify the following parameters, one at a time, and give them different values: | ||
| + | |||
| + | ; theta | ||
| + | : in the main program, change the angle '''theta''' which controls how much a branch will diverge from the direction of the branch that supports it. Try 0.4 first. Then try values between 0 and 0.8. | ||
| + | |||
| + | ; level of recursion | ||
| + | : the main program passes '''9''' to the function as a starting level of recursion. Try passing smaller numbers first, then larger numbers (but less than 13 or so). | ||
| + | |||
| + | ; trunk_ratio | ||
| + | : recursive function defines this as 0.29 and that represents the length of the trunk relative to its two branches. Try ratios between 0.1 (10%) and 0.9 (90%). | ||
| + | |||
| + | <br /> | ||
| + | |||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
| + | =Exploration: Visiting a Maze= | ||
| + | |||
| + | <br /> | ||
| + | <tanbox> | ||
| + | Here is an example of a complex problem that can be (relatively) easily solved using a recursive program. | ||
| + | </tanbox> | ||
| + | <br /> | ||
| + | * Go to [[CSC111 visitMaze.py | this pag]][http://cs.smith.edu/dftwiki/index.php/CSC111_visitMaze.py e], copy the program in the '''Python 3 Graphics''' section. Make sure you have the graphics.py program in the same directory where you will save your program. The name you use for your program does not matter for this lab. | ||
| + | * Run the program. | ||
| + | |||
| + | * Observe how the recursive '''visitMaze()''' function leaves "bread crumbs" as red circles behind the cells that it visits, and colors in grey the cells that lead to impasses. | ||
| + | |||
| + | * Edit the program and switch the order in which the function visits cells in the 4 directions. Make the recursive function decide to go up first, then left, then right, and finally down. | ||
| + | |||
| + | * Run the program and see how this change influences the way the program explores the maze. | ||
| + | |||
| + | * Rename the '''mazeText''' string and call it '''mazeText0'''. | ||
| + | * Rename the '''mazeText1''' string and call it '''mazeText'''. | ||
| + | |||
| + | * Look at '''mazeText''' and predict the path that the program is going to take when visiting it. | ||
| + | |||
| + | * Change the order in which the recursive function visits the different directions, and observe if this modification makes the function find the exit faster. | ||
| + | |||
| + | * Edit '''mazeText''' and put the exit on the left side. Run your program again. Same questions about predicting the path the program takes. | ||
| + | |||
| + | == Treasures in the maze== | ||
| + | |||
| + | * Let's change the rules of the game, and make your program find a path to a treasure, rather than a path to an exit. In our case the treasure will be a special character, say '&', inside the maze, which you can represent as a yellow circle. | ||
| + | |||
| + | * Modify your the visitMaze() function so that it now returns true if it finds the treasure, and false if it doesn't find any treasure. Finding an exit will now not be a condition of success. Verify that your program displays at the end the path to the treasure. | ||
| + | </showafterdate> | ||
<br /> | <br /> | ||
| + | <!-- ====================================================================== --> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | <showafterdate after="20150424 12:00" before="20150601 00:00"> | ||
| + | <br /> | ||
| + | =Solution Programs= | ||
| + | <br /> | ||
| + | <source lang="python"> | ||
| + | # solution programs for Lab12 2015 | ||
| + | # | ||
| + | # | ||
| + | from random import randrange | ||
| + | |||
| + | def fact( n ): | ||
| + | print( "fact function started. Received n =", n ) | ||
| + | print( "testing if %d is >= 1" % (n) ) | ||
| + | |||
| + | if n<=1: | ||
| + | print( "n == 1. Returning 1" ) | ||
| + | return 1 | ||
| + | |||
| + | print( "n > 1. Calling fact( %d )" % (n-1) ) | ||
| + | y = fact( n-1 ) | ||
| + | print( "setting y to %d" % y ) | ||
| + | result = n * y | ||
| + | print( "returning result = %d * %d = %d" % (n, y, n*y) ) | ||
| + | return result | ||
| + | |||
| + | def fact2( n, indent ): | ||
| + | print( indent, "fact2(%d) started" % n ) | ||
| + | print( indent, "comparing %d to 1" % n ) | ||
| + | if n<=1: | ||
| + | print( indent, "%d is <= 1. Returning 1" % 1 ) | ||
| + | return 1 | ||
| + | |||
| + | print( indent, "%d is not <= 1. Calling fact2(%d) and storing it in y" % (n, n-1) ) | ||
| + | y = fact2( n-1, indent + " " ) | ||
| + | print( indent, "just received %d from fact2( %d )." % ( y, n-1 ) ) | ||
| + | result = n * y | ||
| + | print( indent, "multiplied %d by %d. It's %d. Returning %d to caller" % ( n, y, result, result ) ) | ||
| + | return result | ||
| + | |||
| + | def sum1( n ): | ||
| + | if n==1: | ||
| + | return 1 | ||
| + | return n + sum1( n-1 ) | ||
| + | |||
| + | def evenSum1( n ): | ||
| + | if n <= 1: | ||
| + | return 0 | ||
| + | |||
| + | if n%2 == 0: | ||
| + | return n + evenSum1( n-2 ) | ||
| + | if n%2 == 1: | ||
| + | return evenSum1( n-1 ) | ||
| + | |||
| + | def recurseMax( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | return L[0] | ||
| + | |||
| + | return max( L[0], recurseMax( L[1:] ) ) | ||
| + | |||
| + | def divideConquerLargest( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | return L[0] | ||
| + | |||
| + | return max( divideConquerLargest( L[0:N//2] ), | ||
| + | divideConquerLargest( L[N//2: ] ) ) | ||
| + | |||
| + | def divideConquerMin( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | return L[0] | ||
| + | |||
| + | return min( divideConquerMin( L[0:N//2] ), | ||
| + | divideConquerMin( L[N//2: ] ) ) | ||
| + | |||
| + | |||
| + | def divideConquerSum( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | return L[0] | ||
| + | |||
| + | return divideConquerSum( L[0:N//2] ) + divideConquerSum( L[N//2: ] ) | ||
| + | |||
| + | |||
| + | def divideConquerAbs( L ): | ||
| + | N = len( L ) | ||
| + | if N==1: | ||
| + | L[0] = abs( L[0] ) | ||
| + | return L | ||
| + | |||
| + | return divideConquerAbs( L[0:N//2] ) + divideConquerAbs( L[N//2: ] ) | ||
| + | |||
| + | |||
| + | #------------------------------------------------------------------ | ||
| + | def createArray( n ): | ||
| + | """Creates a list of n random numbers in sorted order""" | ||
| + | A= [] | ||
| + | for i in range( n ): | ||
| + | A.append( randrange( n * 10 ) ) | ||
| + | |||
| + | A.sort() | ||
| + | return A | ||
| + | |||
| + | #------------------------------------------------------------------ | ||
| + | def binsearch( A, low, high, key ): | ||
| + | """a recursive function that searches the list A to see if | ||
| + | it contains the item key between the indexes "low" and "high". | ||
| + | returns the index where the key was found, or -1 otherwise | ||
| + | """ | ||
| + | |||
| + | print( "low=%10d high=%10d key=%10d" % (low, high, key) ) | ||
| + | |||
| + | if low>high: | ||
| + | return -1 | ||
| + | |||
| + | mid = ( low + high )//2 | ||
| + | if A[mid]==key: | ||
| + | return mid | ||
| + | |||
| + | if key < A[mid]: | ||
| + | return binsearch( A, low, mid-1, key ) | ||
| + | else: | ||
| + | return binsearch( A, mid+1, high, key ) | ||
| + | |||
| + | |||
| + | |||
| + | def main(): | ||
| + | # fact | ||
| + | """ | ||
| + | n = int( input( "Enter a positive number: " ) ) | ||
| + | x = fact( n ) | ||
| + | print( "the factorial of %d is %d." % ( n , x ) ) | ||
| + | """ | ||
| + | |||
| + | # fact2 | ||
| + | """ | ||
| + | n = int( input( "Enter a positive number: " ) ) | ||
| + | x = fact2( n, " " ) | ||
| + | print( "the factorial of %d is %d." % ( n , x ) ) | ||
| + | """ | ||
| + | |||
| + | # sum1 | ||
| + | """ | ||
| + | n = int( input( "Enter a positive number: " ) ) | ||
| + | print( "sum of all numbers from 1 to %d = %d" % (n, sum1(n) ) ) | ||
| + | """ | ||
| + | |||
| + | # evenSum1 | ||
| + | """ | ||
| + | for n in range( 12 ): | ||
| + | print( " n = %d sumEven(%d) returns %d" % (n, n, evenSum1(n) ) ) | ||
| + | """ | ||
| + | |||
| + | # recursive max | ||
| + | """ | ||
| + | L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] | ||
| + | print( "recurseMax( %s ) = %d" % ( L, recurseMax( L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # divideConquerLargest | ||
| + | """ | ||
| + | L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] | ||
| + | print( "divideConquerLargest( %s ) = %d" % (L, divideConquerLargest(L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # divideConquerMin | ||
| + | """ | ||
| + | L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] | ||
| + | print( "divideConquerMin( %s ) = %d" % (L, divideConquerMin(L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # divideConquerSum | ||
| + | """ | ||
| + | L = [1, 2, 3, 10, 101, 100, 100] | ||
| + | print( "divideConquerSum( %s ) = %d" % (L, divideConquerSum(L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # divideConquerAbs | ||
| + | """ | ||
| + | L = [1, 2, 3, -10, -101, 100, 100] | ||
| + | print( "divideConquerAbs( %s ) = %s" % (L, divideConquerAbs(L ) ) ) | ||
| + | """ | ||
| + | |||
| + | # binSearch | ||
| + | #A = createArray( 20 ) | ||
| + | #print( "A = ", A ) | ||
| + | |||
| + | A = createArray( 1000000 ) | ||
| + | print( A[100:110] ) | ||
| + | |||
| + | while True: | ||
| + | print | ||
| + | key = int( input( "search for what number? " ) ) | ||
| + | if key==-1: break | ||
| + | index = binsearch( A, 0, len( A )-1, key ) | ||
| + | if index != -1: | ||
| + | print( "found %d at index %d" % ( key, index ) ) | ||
| + | else: | ||
| + | print( "%d not in A" % key ) | ||
| + | main() | ||
| + | |||
| + | </source> | ||
| + | <br /> | ||
| + | ==Mazes and Treasures== | ||
| + | <br /> | ||
| + | ::<source lang="python"> | ||
| + | # graphicsVisitMaze.py | ||
| + | # D. Thiebaut | ||
| + | # Generates a maze and displays it in a graphics window. | ||
| + | # The maze is defined as a collection of lines of text. | ||
| + | # MazeText is the variable containing the raw definition. | ||
| + | # MazeText is split into lines and the list of lines is kept | ||
| + | # in the variable maze. | ||
| + | # Each line in mazeText contains # or . characters. A #-character | ||
| + | # indicates a wall, while a . indicates an empty space. | ||
| + | # MazeText is cleaned up and all the dots are replaced by spaces. | ||
| + | # Then the maze is displayed in the graphic window. | ||
| + | # The program maintains the status of the visit in the variable | ||
| + | # maze. A '.' will represent a breadcrumb, i.e. a place that has | ||
| + | # been visited and that is potentially on the path to the exit. An | ||
| + | # 'i' character indicates a visited place that leads to an impass. | ||
| + | # The program starts by visiting location STARTi (line number) | ||
| + | # and STARTj (column number). | ||
| + | # | ||
| + | import time | ||
| + | import os | ||
| + | from graphics import * | ||
| + | |||
| + | |||
| + | # Dimensions of the graphics window | ||
| + | WIDTH = 800 | ||
| + | HEIGHT = 600 | ||
| + | |||
| + | mazeText = """ | ||
| + | ######################### | ||
| + | .............&..........# | ||
| + | ##############.########## | ||
| + | ..#.#........#.#........# | ||
| + | #.#.#.########.########.# | ||
| + | #.#.#.................#.# | ||
| + | #.#.###.#####.#####.#...# | ||
| + | #...........#.#&#.#.##### | ||
| + | #.#########.#.#.#.#.....# | ||
| + | #.#.#.#.#.#.#.#.#######.# | ||
| + | #.#.........#.#.......#.# | ||
| + | #.###############.#####.# | ||
| + | #...............#.......# | ||
| + | #.###########.#########.# | ||
| + | #........#..............# | ||
| + | ######################### | ||
| + | """ | ||
| + | |||
| + | mazeText1 = """ | ||
| + | ######################### | ||
| + | ........................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #........................ | ||
| + | #.......................# | ||
| + | ######################### | ||
| + | """ | ||
| + | |||
| + | mazeText2 = """ | ||
| + | ######################### | ||
| + | ........................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #######################.# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #.####################### | ||
| + | #.......................# | ||
| + | #.......................# | ||
| + | #........................ | ||
| + | #.......................# | ||
| + | ######################### | ||
| + | """ | ||
| + | |||
| + | # | ||
| + | STARTi = 1 # line number | ||
| + | STARTj = 0 # column number | ||
| + | |||
| + | NOLINES = len( mazeText.strip().split("\n") ) | ||
| + | NOCHARS = len( mazeText.strip().split("\n")[1] ) | ||
| + | BLOCKWIDTH = WIDTH // NOCHARS | ||
| + | BLOCKHEIGHT = HEIGHT / NOLINES | ||
| + | |||
| + | |||
| + | def getMazeFromFile( fileName ): | ||
| + | """reads the definition of the maze from a file""" | ||
| + | |||
| + | try: | ||
| + | lines = open( fileName, 'r' ).read() | ||
| + | except: | ||
| + | print( "I/O Error: could not open", fileName ) | ||
| + | return None | ||
| + | |||
| + | return getMaze( lines ) | ||
| + | |||
| + | def getMaze( mazeText ): | ||
| + | """take the string representing the maze and | ||
| + | break it down into an array of lines""" | ||
| + | maze=[] | ||
| + | for i, line in enumerate( mazeText.split( '\n' ) ): | ||
| + | line = line.strip() | ||
| + | #print( "%d [%s]" % (i, line ) ) | ||
| + | if len( line ) < 2: | ||
| + | continue | ||
| + | line = line.replace( '.', ' ' ) | ||
| + | maze.append( line ) | ||
| + | return maze | ||
| + | |||
| + | def printMaze( maze ): | ||
| + | for line in maze: | ||
| + | print( line ) | ||
| + | for i in range( len( maze ) ): | ||
| + | for j in range( len( maze[0] ) ): | ||
| + | print( maze[i][j], sep="", end="" ) | ||
| + | print() | ||
| + | print() | ||
| + | |||
| + | def setBreakCrumb( i, j, win ): | ||
| + | global BLOCKWIDTH | ||
| + | global BLOCKHEIGHT | ||
| + | radius = BLOCKWIDTH // 4 | ||
| + | brd = Circle( Point( (j+0.5)*BLOCKWIDTH, (i+0.5)*BLOCKHEIGHT ), radius ) | ||
| + | brd.setFill( "red" ) | ||
| + | brd.draw( win ) | ||
| + | |||
| + | # rest a tiny bit to slow down the program | ||
| + | time.sleep( 0.1 ) | ||
| + | |||
| + | def setTreasure( i, j, win ): | ||
| + | global BLOCKWIDTH | ||
| + | global BLOCKHEIGHT | ||
| + | radius = BLOCKWIDTH // 4 | ||
| + | brd = Circle( Point( (j+0.5)*BLOCKWIDTH, (i+0.5)*BLOCKHEIGHT ), radius ) | ||
| + | brd.setFill( "orange" ) | ||
| + | brd.draw( win ) | ||
| + | |||
| + | |||
| + | def setImpass( i, j, win ): | ||
| + | global BLOCKWIDTH | ||
| + | global BLOCKHEIGHT | ||
| + | radius = BLOCKWIDTH // 4 | ||
| + | blk = Rectangle( Point( j*BLOCKWIDTH, i*BLOCKHEIGHT ), | ||
| + | Point( (j+1)*BLOCKWIDTH, (i+1)*BLOCKHEIGHT ) ) | ||
| + | blk.setFill( "lightgrey" ) | ||
| + | blk.setOutline( "lightgrey" ) | ||
| + | blk.draw( win ) | ||
| + | |||
| + | # rest a tiny bit to slow down the program | ||
| + | time.sleep( 0.1 ) | ||
| + | |||
| + | |||
| + | def displayMaze( maze, win ): | ||
| + | """ display the maze and wait for some amount of time""" | ||
| + | global BLOCKWIDTH | ||
| + | global BLOCKHEIGHT | ||
| + | global NOLINES | ||
| + | global NOCHARS | ||
| + | |||
| + | blocks = [] | ||
| + | for i in range (NOLINES ): | ||
| + | for j in range( NOCHARS ): | ||
| + | if maze[i][j]=="#": | ||
| + | r = Rectangle( Point( j*BLOCKWIDTH, i*BLOCKHEIGHT ), | ||
| + | Point( (j+1)*BLOCKWIDTH, (i+1)*BLOCKHEIGHT ) ) | ||
| + | r.setFill( "blue" ) | ||
| + | r.setOutline( "blue" ) | ||
| + | r.draw( win ) | ||
| + | blocks.append( r ) | ||
| + | if maze[i][j]=="&": | ||
| + | setTreasure( i, j, win ) | ||
| + | |||
| + | return blocks | ||
| + | |||
| + | def setChar( maze, i, j, char ): | ||
| + | """puts the character char at position i, | ||
| + | j in the maze""" | ||
| + | line = maze[i] | ||
| + | letters = [] | ||
| + | for letter in line: | ||
| + | letters.append( letter ) | ||
| + | letters[j] = char | ||
| + | maze[i] = ''.join( letters ) | ||
| + | |||
| + | def visitMaze( maze, i, j, win ): | ||
| + | """recursive visit of the maze. Returns True when it | ||
| + | has found the exit, False otherwise""" | ||
| + | |||
| + | print( "visiting cell( %d, %d) containing '%s'" | ||
| + | % (i, j, maze[i][j] ) ) | ||
| + | |||
| + | #printMaze( maze ) | ||
| + | if ( i != STARTi or j != STARTj ) and maze[i][j]=='&': | ||
| + | #and ( (i==0 or i==len( maze )-1 ) or (j==0 or j==len( maze[0] )-1 ) ): | ||
| + | return True | ||
| + | |||
| + | # put a bread crum where we are | ||
| + | setBreakCrumb( i, j, win ) | ||
| + | setChar( maze, i, j, '.' ) | ||
| + | |||
| + | #--- try the four directions around where we are --- | ||
| + | #--- to the right? --- | ||
| + | if j+1< len( maze[0] ) and maze[i][j+1] in " &": | ||
| + | if visitMaze( maze, i, j+1, win ) == True: | ||
| + | return True # found an exit by going right! | ||
| + | |||
| + | #--- down? --- | ||
| + | if i+1< len( maze ) and maze[i+1][j] in " &": | ||
| + | if visitMaze( maze, i+1, j, win ) == True: | ||
| + | return True # found an exit by going down! | ||
| + | |||
| + | #--- up? --- | ||
| + | if i-1>=0 and maze[i-1][j] in " &": | ||
| + | if visitMaze( maze, i-1, j, win ) == True: | ||
| + | return True # found an exit by going up! | ||
| + | |||
| + | #--- to the left? --- | ||
| + | if j-1>=0 and maze[i][j-1] in " &": | ||
| + | if visitMaze( maze, i, j-1, win ) == True: | ||
| + | return True # found an exit by going left! | ||
| + | |||
| + | #--- if we're here, none of the 4 directions was successful --- | ||
| + | #--- in bringing us to an exit, we have to mark our cell with-- | ||
| + | #--- a v, and return false to our caller, indicating that we--- | ||
| + | #--- couldn't find a path --- | ||
| + | |||
| + | setImpass( i, j, win ) | ||
| + | setChar( maze, i, j, 'v' ) | ||
| + | #printMaze( maze ) | ||
| + | return False | ||
| + | |||
| + | |||
| + | def main(): | ||
| + | """gets the maze, visit and display it""" | ||
| + | #maze = getMazeFromFile( 'largemaze.txt' ) | ||
| + | win = GraphWin("Maze", WIDTH, HEIGHT ) | ||
| + | |||
| + | maze = getMaze( mazeText ) | ||
| + | |||
| + | #printMaze( maze ) | ||
| + | blocks = displayMaze( maze, win ) | ||
| + | printMaze( maze ) | ||
| + | success = visitMaze( maze, STARTi, STARTj, win ) | ||
| + | |||
| + | #--- print the maze without the v-characters --- | ||
| + | #printMazeNoVs( maze ) | ||
| + | |||
| + | if success: | ||
| + | print( "A path was found!" ) | ||
| + | else: | ||
| + | print( "No path to an exit found..." ) | ||
| + | |||
| + | win.getMouse() | ||
| + | win.close() | ||
| + | |||
| + | main() | ||
| + | </source> | ||
| + | <br /> | ||
| + | </showafterdate> | ||
| + | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
Latest revision as of 06:31, 22 April 2015
--D. Thiebaut (talk) 11:31, 19 April 2015 (EDT)
|
This lab deals with recursive functions. Programming recursive functions is a challenging concept to master. The best way to proceed is to write many different recursive solutions and observe the behavior of the functions as they perform their work. Eventually recursion will start making sense. It is normal to not fully understand it at first. Keep at it. Little by little, it will become natural thinking.
|
<showafterdate after="20150422 12:00" before="20150601 00:00">
Visualizing Recursive Factorial At Work
Create a copy of this simple example:
# factorial.py # Demonstrates a recursive factorial function def fact( n ): # stopping condition if n<=1: return 1 # recursive step y = fact( n-1 ) result = n * y return result def main(): n = int( input( "Enter a positive number: " ) ) x = fact( n ) print( "the factorial of %d is %d." % ( n , x ) ) main()
- Run your program
- It will prompt you for a number and will return its factorial.
- Verify that it computes the correct result. Below are some factorials numbers to compare your output to.
1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 6! = 720 7! = 5040 8! = 40320 9! = 362880 10! = 3628800 11! = 39916800 12! = 479001600 13! = 6227020800 14! = 87178291200
Visualizing, Step 1
- Add print statements to your fact() function so that it will let you know exactly what it does. For example, before it tests to see if n is less than equal to 1, you could print:
print( "fact function started. Receives n =", n )
print( "testing if %d is >= 1" % (n) )
- Add print statements that will show the values of y and result.
- Run your program and observe its output. Can you see better how the function fact() recursively calls itself?
Visualizing, Step 2
- Create the more sophisticated program shown below. Observe it well first, and try to figure out what the indent variable does.
# factorialPrint.py # Demonstrates a recursive factorial function def fact2( n, indent ): print( indent, "fact2(%d) started" % n ) print( indent, "comparing %d to 1" % n ) if n<=1: print( indent, "%d is <= 1. Returning 1" % 1 ) return 1 print( indent, "%d is not <= 1. Calling fact2(%d) and storing it in y" % (n, n-1) ) y = fact2( n-1, indent + " " ) print( indent, "just received %d from fact2( %d )." % ( y, n-1 ) ) result = n * y print( indent, "multiplied %d by %d. It's %d. Returning %d to caller" % ( n, y, result, result ) ) return result def main(): n = int( input( "Enter a positive integer: " ) ) print( "Main calls fact( %d )" % n ) y = fact2( n, " " ) print( "Main receives result = ", y ) main()
- Run the program
- Explain the pattern made by the printed lines. Why this shape?
- Where does the stopping condition appear in the printed lines? In other words, where is the printed statement that indicates that fact() just received a value of n equal to 1? Why isn't this statement at the end of the printout?
Thinking Recursively
All the challenges below require you to put together a recursive function for a simple problem.
Thinking recursively is quite challenging and takes a while to master. So don't despair!
Here are points to remember when building a recursive function:
- First, figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's what it should expect to receive back from a call to itself.
- What is the stopping condition? What is the smallest problem you can solve without recursion? That's the first thing you want to test for and do in your recursive function.
- If the stopping condition doesn't apply, and the function has to do some work, figure out how to make one or several recursive calls to the function, get some intermediate results back, combine them together and get the final answer. That's the recursive step.
- First, figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's what it should expect to receive back from a call to itself.
Challenge 1: Recursive Sum |
- Given a number n, compute recursively the sum of all the numbers from 1 to n. For example, if you pass n = 5 to the solution function, it will return 15 (which is equal to 5+4+3+2+1)
Challenge 2: Recursive Even Sum |
- Given a number n, compute recursively the sum of all the positive even numbers less than or equal to n.
- This is trickier than it seems! Here is an example of running a loop and asking the recursive function to compute the sum of all the even numbers up to n when n ranges from 0 to 12.
n = 0 sumEven(0) returns 0 n = 1 sumEven(1) returns 0 n = 2 sumEven(2) returns 2 n = 3 sumEven(3) returns 2 n = 4 sumEven(4) returns 6 n = 5 sumEven(5) returns 6 n = 6 sumEven(6) returns 12 n = 7 sumEven(7) returns 12 n = 8 sumEven(8) returns 20 n = 9 sumEven(9) returns 20 n = 10 sumEven(10) returns 30 n = 11 sumEven(11) returns 30
Challenge 3: Recursive Max |
- Write a recursive function that returns the largest element of a list L using the following formula:
|
largest( L ) |
= L[0] |
if len( L ) == 1 |
|
|
= max( L[0], largest( L[1:] ) ) |
otherwise. We assume N=len(L) |
- Test your program on different lists of varying sizes. We assume that the lists will always have at least one element.
- Hints
- the function definition is simply def largest( L ):
- write the stopping condition first (if len(L)...)
- if the stopping condition is not met, compute the max() of L[0] and largest( L minus the first element )
def largest( A ):
if len( A )==1:
return A[0]
return max( A[0], largest( A[1:] ) )
Divide and Conquer Recursion
- We now take a slightly different approach. This time we take a list, divide it two halves, recursively process the two halves, and combine the result of the results obtained on both sides.
- As an example, assume we have to find the largest item in a list L. Here's a possible way to describe the recursive divide-and-conquer approach:
|
largest( L ) |
= L[0] |
if len( L ) == 1 |
|
|
= max( largest( L[0:N/2], largest( L[N/2:] ) ) |
otherwise. We assume N=len(L) |
The code equivalent to this definition is shown below:
def divideConquerLargest( L ): N = len( L ) if N==1: return L[0] return max( divideConquerLargest( L[0:N//2] ), divideConquerLargest( L[N//2: ] ) )
- Run this code, and verify that it returns the largest element of an unsorted list of integers.
L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] print( "divideConquerLargest( %s ) = %d" % (L, divideConquerLargest(L ) ) )
Challenge 4: Divide-and-Conquer Min |
- Write a recursive function that uses the divide and conquer approach to find the smallest element in a list L.
Challenge 5: Divide-and-Conquer Sum |
- Write a recursive function that uses the divide and conquer approach to compute the sum of all the elements in a list L.
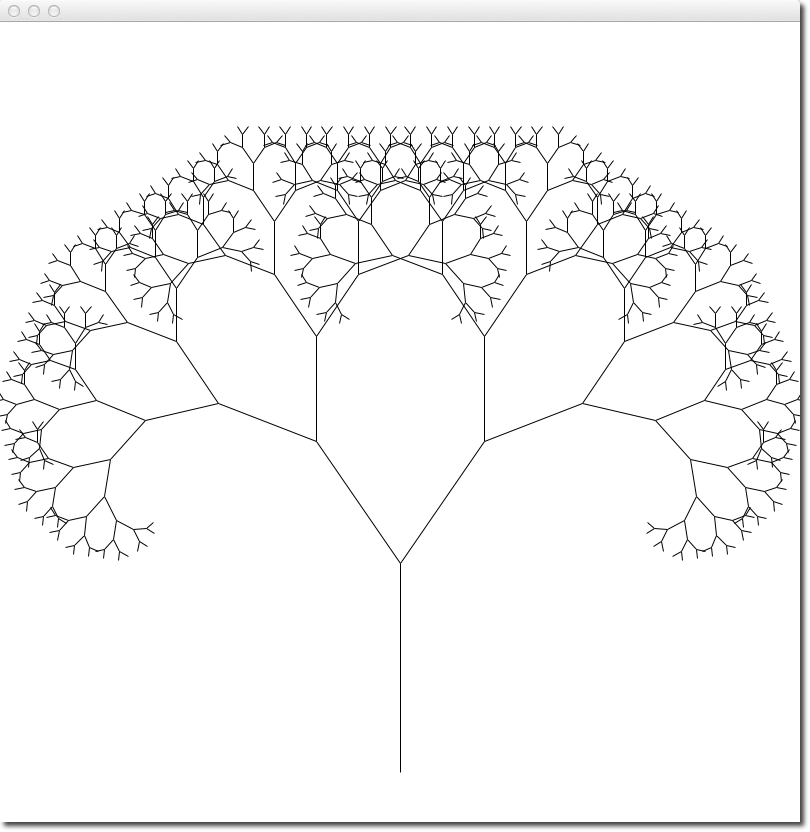
Fractal Trees
- This exercise is for you to explore recursion in the context of graphics.
- Create a new program with the code you'll find on this page, put it in the same directory where you store your graphics.py directory. You may want to call your program fractalTree.py.
- The program will generate a fractal tree. Fractals are self-similar objects: they look the same on a small scale as they do on a larger scale.
- Run the program first.
- Look at the code and see if you can figure out how the recursion works.
- To see how the different parameters influence the drawing of the fractal tree, modify the following parameters, one at a time, and give them different values:
- theta
- in the main program, change the angle theta which controls how much a branch will diverge from the direction of the branch that supports it. Try 0.4 first. Then try values between 0 and 0.8.
- level of recursion
- the main program passes 9 to the function as a starting level of recursion. Try passing smaller numbers first, then larger numbers (but less than 13 or so).
- trunk_ratio
- recursive function defines this as 0.29 and that represents the length of the trunk relative to its two branches. Try ratios between 0.1 (10%) and 0.9 (90%).
Exploration: Visiting a Maze
Here is an example of a complex problem that can be (relatively) easily solved using a recursive program.
- Go to this page, copy the program in the Python 3 Graphics section. Make sure you have the graphics.py program in the same directory where you will save your program. The name you use for your program does not matter for this lab.
- Run the program.
- Observe how the recursive visitMaze() function leaves "bread crumbs" as red circles behind the cells that it visits, and colors in grey the cells that lead to impasses.
- Edit the program and switch the order in which the function visits cells in the 4 directions. Make the recursive function decide to go up first, then left, then right, and finally down.
- Run the program and see how this change influences the way the program explores the maze.
- Rename the mazeText string and call it mazeText0.
- Rename the mazeText1 string and call it mazeText.
- Look at mazeText and predict the path that the program is going to take when visiting it.
- Change the order in which the recursive function visits the different directions, and observe if this modification makes the function find the exit faster.
- Edit mazeText and put the exit on the left side. Run your program again. Same questions about predicting the path the program takes.
Treasures in the maze
- Let's change the rules of the game, and make your program find a path to a treasure, rather than a path to an exit. In our case the treasure will be a special character, say '&', inside the maze, which you can represent as a yellow circle.
- Modify your the visitMaze() function so that it now returns true if it finds the treasure, and false if it doesn't find any treasure. Finding an exit will now not be a condition of success. Verify that your program displays at the end the path to the treasure.
</showafterdate>
<showafterdate after="20150424 12:00" before="20150601 00:00">
Solution Programs
# solution programs for Lab12 2015
#
#
from random import randrange
def fact( n ):
print( "fact function started. Received n =", n )
print( "testing if %d is >= 1" % (n) )
if n<=1:
print( "n == 1. Returning 1" )
return 1
print( "n > 1. Calling fact( %d )" % (n-1) )
y = fact( n-1 )
print( "setting y to %d" % y )
result = n * y
print( "returning result = %d * %d = %d" % (n, y, n*y) )
return result
def fact2( n, indent ):
print( indent, "fact2(%d) started" % n )
print( indent, "comparing %d to 1" % n )
if n<=1:
print( indent, "%d is <= 1. Returning 1" % 1 )
return 1
print( indent, "%d is not <= 1. Calling fact2(%d) and storing it in y" % (n, n-1) )
y = fact2( n-1, indent + " " )
print( indent, "just received %d from fact2( %d )." % ( y, n-1 ) )
result = n * y
print( indent, "multiplied %d by %d. It's %d. Returning %d to caller" % ( n, y, result, result ) )
return result
def sum1( n ):
if n==1:
return 1
return n + sum1( n-1 )
def evenSum1( n ):
if n <= 1:
return 0
if n%2 == 0:
return n + evenSum1( n-2 )
if n%2 == 1:
return evenSum1( n-1 )
def recurseMax( L ):
N = len( L )
if N==1:
return L[0]
return max( L[0], recurseMax( L[1:] ) )
def divideConquerLargest( L ):
N = len( L )
if N==1:
return L[0]
return max( divideConquerLargest( L[0:N//2] ),
divideConquerLargest( L[N//2: ] ) )
def divideConquerMin( L ):
N = len( L )
if N==1:
return L[0]
return min( divideConquerMin( L[0:N//2] ),
divideConquerMin( L[N//2: ] ) )
def divideConquerSum( L ):
N = len( L )
if N==1:
return L[0]
return divideConquerSum( L[0:N//2] ) + divideConquerSum( L[N//2: ] )
def divideConquerAbs( L ):
N = len( L )
if N==1:
L[0] = abs( L[0] )
return L
return divideConquerAbs( L[0:N//2] ) + divideConquerAbs( L[N//2: ] )
#------------------------------------------------------------------
def createArray( n ):
"""Creates a list of n random numbers in sorted order"""
A= []
for i in range( n ):
A.append( randrange( n * 10 ) )
A.sort()
return A
#------------------------------------------------------------------
def binsearch( A, low, high, key ):
"""a recursive function that searches the list A to see if
it contains the item key between the indexes "low" and "high".
returns the index where the key was found, or -1 otherwise
"""
print( "low=%10d high=%10d key=%10d" % (low, high, key) )
if low>high:
return -1
mid = ( low + high )//2
if A[mid]==key:
return mid
if key < A[mid]:
return binsearch( A, low, mid-1, key )
else:
return binsearch( A, mid+1, high, key )
def main():
# fact
"""
n = int( input( "Enter a positive number: " ) )
x = fact( n )
print( "the factorial of %d is %d." % ( n , x ) )
"""
# fact2
"""
n = int( input( "Enter a positive number: " ) )
x = fact2( n, " " )
print( "the factorial of %d is %d." % ( n , x ) )
"""
# sum1
"""
n = int( input( "Enter a positive number: " ) )
print( "sum of all numbers from 1 to %d = %d" % (n, sum1(n) ) )
"""
# evenSum1
"""
for n in range( 12 ):
print( " n = %d sumEven(%d) returns %d" % (n, n, evenSum1(n) ) )
"""
# recursive max
"""
L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1]
print( "recurseMax( %s ) = %d" % ( L, recurseMax( L ) ) )
"""
# divideConquerLargest
"""
L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1]
print( "divideConquerLargest( %s ) = %d" % (L, divideConquerLargest(L ) ) )
"""
# divideConquerMin
"""
L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1]
print( "divideConquerMin( %s ) = %d" % (L, divideConquerMin(L ) ) )
"""
# divideConquerSum
"""
L = [1, 2, 3, 10, 101, 100, 100]
print( "divideConquerSum( %s ) = %d" % (L, divideConquerSum(L ) ) )
"""
# divideConquerAbs
"""
L = [1, 2, 3, -10, -101, 100, 100]
print( "divideConquerAbs( %s ) = %s" % (L, divideConquerAbs(L ) ) )
"""
# binSearch
#A = createArray( 20 )
#print( "A = ", A )
A = createArray( 1000000 )
print( A[100:110] )
while True:
print
key = int( input( "search for what number? " ) )
if key==-1: break
index = binsearch( A, 0, len( A )-1, key )
if index != -1:
print( "found %d at index %d" % ( key, index ) )
else:
print( "%d not in A" % key )
main()
Mazes and Treasures
# graphicsVisitMaze.py # D. Thiebaut # Generates a maze and displays it in a graphics window. # The maze is defined as a collection of lines of text. # MazeText is the variable containing the raw definition. # MazeText is split into lines and the list of lines is kept # in the variable maze. # Each line in mazeText contains # or . characters. A #-character # indicates a wall, while a . indicates an empty space. # MazeText is cleaned up and all the dots are replaced by spaces. # Then the maze is displayed in the graphic window. # The program maintains the status of the visit in the variable # maze. A '.' will represent a breadcrumb, i.e. a place that has # been visited and that is potentially on the path to the exit. An # 'i' character indicates a visited place that leads to an impass. # The program starts by visiting location STARTi (line number) # and STARTj (column number). # import time import os from graphics import * # Dimensions of the graphics window WIDTH = 800 HEIGHT = 600 mazeText = """ ######################### .............&..........# ##############.########## ..#.#........#.#........# #.#.#.########.########.# #.#.#.................#.# #.#.###.#####.#####.#...# #...........#.#&#.#.##### #.#########.#.#.#.#.....# #.#.#.#.#.#.#.#.#######.# #.#.........#.#.......#.# #.###############.#####.# #...............#.......# #.###########.#########.# #........#..............# ######################### """ mazeText1 = """ ######################### ........................# #.......................# #.......................# #.......................# #.......................# #.......................# #.......................# #.......................# #.......................# #.......................# #.......................# #.......................# #.......................# #........................ #.......................# ######################### """ mazeText2 = """ ######################### ........................# #.......................# #.......................# #.......................# #.......................# #.......................# #.......................# #######################.# #.......................# #.......................# #.......................# #.......................# #.####################### #.......................# #.......................# #........................ #.......................# ######################### """ # STARTi = 1 # line number STARTj = 0 # column number NOLINES = len( mazeText.strip().split("\n") ) NOCHARS = len( mazeText.strip().split("\n")[1] ) BLOCKWIDTH = WIDTH // NOCHARS BLOCKHEIGHT = HEIGHT / NOLINES def getMazeFromFile( fileName ): """reads the definition of the maze from a file""" try: lines = open( fileName, 'r' ).read() except: print( "I/O Error: could not open", fileName ) return None return getMaze( lines ) def getMaze( mazeText ): """take the string representing the maze and break it down into an array of lines""" maze=[] for i, line in enumerate( mazeText.split( '\n' ) ): line = line.strip() #print( "%d [%s]" % (i, line ) ) if len( line ) < 2: continue line = line.replace( '.', ' ' ) maze.append( line ) return maze def printMaze( maze ): for line in maze: print( line ) for i in range( len( maze ) ): for j in range( len( maze[0] ) ): print( maze[i][j], sep="", end="" ) print() print() def setBreakCrumb( i, j, win ): global BLOCKWIDTH global BLOCKHEIGHT radius = BLOCKWIDTH // 4 brd = Circle( Point( (j+0.5)*BLOCKWIDTH, (i+0.5)*BLOCKHEIGHT ), radius ) brd.setFill( "red" ) brd.draw( win ) # rest a tiny bit to slow down the program time.sleep( 0.1 ) def setTreasure( i, j, win ): global BLOCKWIDTH global BLOCKHEIGHT radius = BLOCKWIDTH // 4 brd = Circle( Point( (j+0.5)*BLOCKWIDTH, (i+0.5)*BLOCKHEIGHT ), radius ) brd.setFill( "orange" ) brd.draw( win ) def setImpass( i, j, win ): global BLOCKWIDTH global BLOCKHEIGHT radius = BLOCKWIDTH // 4 blk = Rectangle( Point( j*BLOCKWIDTH, i*BLOCKHEIGHT ), Point( (j+1)*BLOCKWIDTH, (i+1)*BLOCKHEIGHT ) ) blk.setFill( "lightgrey" ) blk.setOutline( "lightgrey" ) blk.draw( win ) # rest a tiny bit to slow down the program time.sleep( 0.1 ) def displayMaze( maze, win ): """ display the maze and wait for some amount of time""" global BLOCKWIDTH global BLOCKHEIGHT global NOLINES global NOCHARS blocks = [] for i in range (NOLINES ): for j in range( NOCHARS ): if maze[i][j]=="#": r = Rectangle( Point( j*BLOCKWIDTH, i*BLOCKHEIGHT ), Point( (j+1)*BLOCKWIDTH, (i+1)*BLOCKHEIGHT ) ) r.setFill( "blue" ) r.setOutline( "blue" ) r.draw( win ) blocks.append( r ) if maze[i][j]=="&": setTreasure( i, j, win ) return blocks def setChar( maze, i, j, char ): """puts the character char at position i, j in the maze""" line = maze[i] letters = [] for letter in line: letters.append( letter ) letters[j] = char maze[i] = ''.join( letters ) def visitMaze( maze, i, j, win ): """recursive visit of the maze. Returns True when it has found the exit, False otherwise""" print( "visiting cell( %d, %d) containing '%s'" % (i, j, maze[i][j] ) ) #printMaze( maze ) if ( i != STARTi or j != STARTj ) and maze[i][j]=='&': #and ( (i==0 or i==len( maze )-1 ) or (j==0 or j==len( maze[0] )-1 ) ): return True # put a bread crum where we are setBreakCrumb( i, j, win ) setChar( maze, i, j, '.' ) #--- try the four directions around where we are --- #--- to the right? --- if j+1< len( maze[0] ) and maze[i][j+1] in " &": if visitMaze( maze, i, j+1, win ) == True: return True # found an exit by going right! #--- down? --- if i+1< len( maze ) and maze[i+1][j] in " &": if visitMaze( maze, i+1, j, win ) == True: return True # found an exit by going down! #--- up? --- if i-1>=0 and maze[i-1][j] in " &": if visitMaze( maze, i-1, j, win ) == True: return True # found an exit by going up! #--- to the left? --- if j-1>=0 and maze[i][j-1] in " &": if visitMaze( maze, i, j-1, win ) == True: return True # found an exit by going left! #--- if we're here, none of the 4 directions was successful --- #--- in bringing us to an exit, we have to mark our cell with-- #--- a v, and return false to our caller, indicating that we--- #--- couldn't find a path --- setImpass( i, j, win ) setChar( maze, i, j, 'v' ) #printMaze( maze ) return False def main(): """gets the maze, visit and display it""" #maze = getMazeFromFile( 'largemaze.txt' ) win = GraphWin("Maze", WIDTH, HEIGHT ) maze = getMaze( mazeText ) #printMaze( maze ) blocks = displayMaze( maze, win ) printMaze( maze ) success = visitMaze( maze, STARTi, STARTj, win ) #--- print the maze without the v-characters --- #printMazeNoVs( maze ) if success: print( "A path was found!" ) else: print( "No path to an exit found..." ) win.getMouse() win.close() main()
</showafterdate>