Difference between revisions of "CSC231 Lab 3 (Digital Electronics)"
(→3-Bit Adder) |
(→3-Bit Adder) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | © D. Thiebaut, 2010 | ||
| Line 9: | Line 10: | ||
<br /> | <br /> | ||
| − | + | <bluebox>This lab is the continuation of [[CSC231 Lab 2 (Digital Electronics) | Lab 2]] | |
| − | + | ||
| + | </bluebox> | ||
| + | |||
| + | =Preamble= | ||
| + | |||
| + | * Assume that we have two boolean variables, a and b. How could you prove that the following equality always holds? | ||
| + | |||
| + | a + a'. b = a + b | ||
| + | |||
| + | :(a' represents ''not'' a ) | ||
| + | |||
| + | =3-Bit Adder= | ||
| + | |||
| + | * Write down all 8 possible additions of 3 bits, and show the two bits that result: ''Carry'' and ''Sum'', in a manner similar to the example below | ||
| + | |||
| + | <source lang="text"> | ||
| + | 0 | ||
| + | + 0 | ||
| + | + 0 | ||
| + | ------ | ||
| + | X X | ||
| + | </source> | ||
| + | |||
| + | * Fill out the truth table below where '''a''', '''b''', and '''d''' are the three bits that are added together, '''C''' is the carry, and '''S''' the sum. | ||
| + | |||
| + | |||
| + | |||
| + | <source lang="text"> | ||
| + | a b d | C S | ||
| + | -----------+-------- | ||
| + | 0 0 0 | | ||
| + | 0 0 1 | | ||
| + | 0 1 0 | | ||
| + | 0 1 1 | | ||
| + | 1 0 0 | | ||
| + | 1 0 1 | | ||
| + | 1 1 0 | | ||
| + | 1 1 1 | | ||
| + | </source> | ||
| + | |||
| + | |||
| + | * Generate the boolean expressions for C and S. This steps will require the whole class to work together! Keep on simplifying until you find an expression for S with only 2 operators, and an expression for C with only 5 operators! | ||
| + | |||
| + | * Generate the schematics for the circuit generating C and S | ||
| + | |||
| + | * Use the data sheets provided to assign pin numbers to the gates. | ||
| + | |||
| + | * Wire it up and demonstrate that you can correctly add 3 bits together! | ||
| + | |||
| + | =Useful Gates= | ||
| + | {| | ||
| + | | | ||
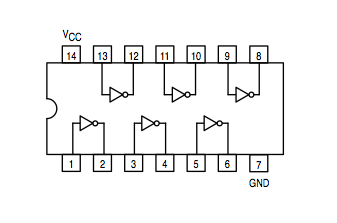
| + | [[Image:7404.png]] | ||
| + | | | ||
| + | Inverter: 74LS04 | ||
| + | |- | ||
| + | | | ||
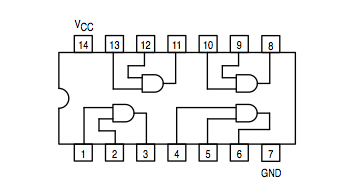
| + | [[Image:7408.png]] | ||
| + | | | ||
| + | AND gate: 74LS08 | ||
| + | |- | ||
| + | | | ||
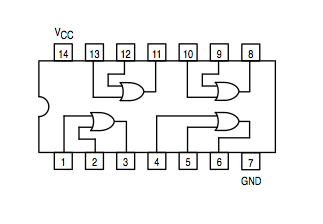
| + | [[Image:7432.png]] | ||
| + | | | ||
| + | OR gate: 74LS32 | ||
| + | |- | ||
| + | | | ||
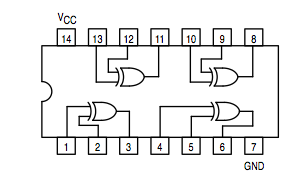
| + | [[Image:7486.png]] | ||
| + | | | ||
| + | Exclusive OR: 74LS86 | ||
| + | |} | ||
| − | + | =Data Sheets= | |
If you need to refer to the data sheets of various chips during the lab, you can click on any of the links below: | If you need to refer to the data sheets of various chips during the lab, you can click on any of the links below: | ||
| Line 61: | Line 132: | ||
[http://cs.smith.edu/~thiebaut/classes/270/datasheets/DM74LS259.pdf 74LS25] | [http://cs.smith.edu/~thiebaut/classes/270/datasheets/DM74LS259.pdf 74LS25] | ||
[http://cs.smith.edu/~thiebaut/classes/270/datasheets/CD74hct541.pdf 74HCT54]. | [http://cs.smith.edu/~thiebaut/classes/270/datasheets/CD74hct541.pdf 74HCT54]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
Latest revision as of 06:41, 18 November 2014
© D. Thiebaut, 2010
Back to the weekly schedule
This lab is the continuation of Lab 2
Preamble
- Assume that we have two boolean variables, a and b. How could you prove that the following equality always holds?
a + a'. b = a + b
- (a' represents not a )
3-Bit Adder
- Write down all 8 possible additions of 3 bits, and show the two bits that result: Carry and Sum, in a manner similar to the example below
0
+ 0
+ 0
------
X X
- Fill out the truth table below where a, b, and d are the three bits that are added together, C is the carry, and S the sum.
a b d | C S
-----------+--------
0 0 0 |
0 0 1 |
0 1 0 |
0 1 1 |
1 0 0 |
1 0 1 |
1 1 0 |
1 1 1 |
- Generate the boolean expressions for C and S. This steps will require the whole class to work together! Keep on simplifying until you find an expression for S with only 2 operators, and an expression for C with only 5 operators!
- Generate the schematics for the circuit generating C and S
- Use the data sheets provided to assign pin numbers to the gates.
- Wire it up and demonstrate that you can correctly add 3 bits together!
Useful Gates
|
Inverter: 74LS04 | |
|
AND gate: 74LS08 | |
|
OR gate: 74LS32 | |
|
Exclusive OR: 74LS86 |
Data Sheets
If you need to refer to the data sheets of various chips during the lab, you can click on any of the links below: If the datasheets haven't been printed yet, print a set from these links: 74LS00 74LS01 74LS02 74LS03 74LS04 74LS05 74LS08 74LS09 74LS10 74LS12 74LS13 74LS15 74LS20 74LS21 74LS22 74LS26 74LS27 74LS28 74LS30 74LS32 74LS33 74LS37 74LS38 74LS40 74LS42 74LS47 74LS48 74LS51 74LS54 74LS55 74LS74 74LS75 74LS76 74LS83 74LS85 74LS86 74LS90 74LS9 74LS13 74HCT24 74LS24 74HCT24 74LS25 74HCT54.