Difference between revisions of "CSC231 Exercises with Signed Numbers"
| Line 98: | Line 98: | ||
=Solutions= | =Solutions= | ||
<onlydft> | <onlydft> | ||
| − | ==Problem # | + | ==Problem #3== |
0 = 0000 0000 in all 3 systems | 0 = 0000 0000 in all 3 systems | ||
| Line 124: | Line 124: | ||
= 1000 0000 in 2's complement, but, again, that's not possible ==> can't represent 128 in 2's complement | = 1000 0000 in 2's complement, but, again, that's not possible ==> can't represent 128 in 2's complement | ||
| − | ==Problem # | + | ==Problem #4== |
0000 0000 0000 0001 = 1 | 0000 0000 0000 0001 = 1 | ||
| Line 137: | Line 137: | ||
The all-1 bit pattern is therefore the representation of -1 | The all-1 bit pattern is therefore the representation of -1 | ||
| − | ==Problem # | + | ==Problem #5== |
::(for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary) | ::(for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary) | ||
| Line 159: | Line 159: | ||
= 77. It works! | = 77. It works! | ||
| + | ==Problem #6== | ||
| + | * 125 is 0111 1101. | ||
| + | * -125 is 1000 0011 | ||
| + | * In 2's complement, the most significant bit of an 8-bit word has weight -128. Why? Because 1000 0000 is -128 in 2's complement. So when we see -125, it's really the result of saying "these bits represent -128 + 3. But if this were an unsigned number, the value would be +128 + 3 = 131. Another way of saying this, is that if we add 256 to -125, we get 131. So, very likely, the temperature we should have see is 131 degrees. | ||
</onlydft> | </onlydft> | ||
Revision as of 08:10, 3 October 2012
--D. Thiebaut 09:37, 1 October 2012 (EDT)
Binary Addition in Various Systems
Exercise 1
What is the range of numbers in a 4-bit unsigned system? in a 4-bit 2's complement system? in an 8-bit unsigned system? In an 8-bit 2's complement system?
(Revisit the handout on Java's range of data types.)
Exercise 2
An program written in some unspecified language contains an array of 10 bytes. The values of the 10 bytes are 0x10, 0xff, 0xf1, 0x00, 0x00, 0xfe, 0x73, 0x01, 0x02, 0x7f.
Are these values used to represent signed numbers, unsigned numbers, numbers in 2's complement, numbers in 1's complement, or numbers in signed magnitude?
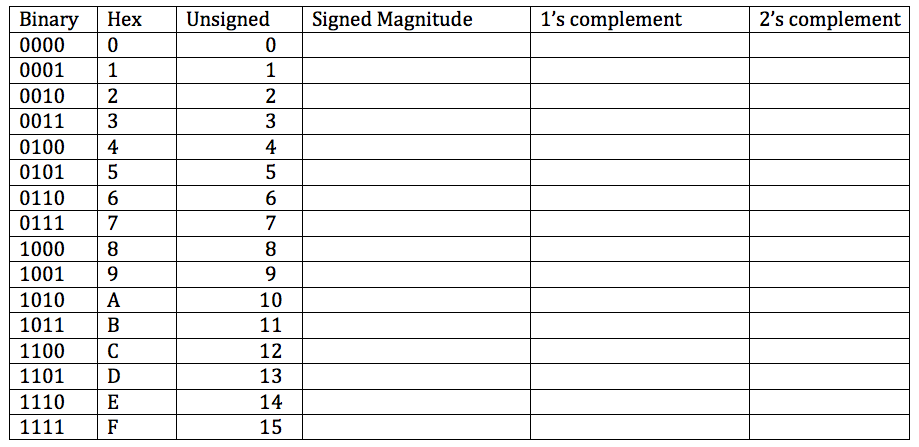
Exercise 3
- what is the 8-bit representation of the following decimal numbers in signed magnitude, 1's complement, and 2's complement?
0 1 -1 11 -11 127 -127 128 -128
Exercise #4
- Convert the following signed, 2's complement 16-bit binary numbers to their decimal equivalent.
0000 0000 0000 0001 1000 0000 0000 0001 0000 0000 1111 1111 1111 1111 1111 1111
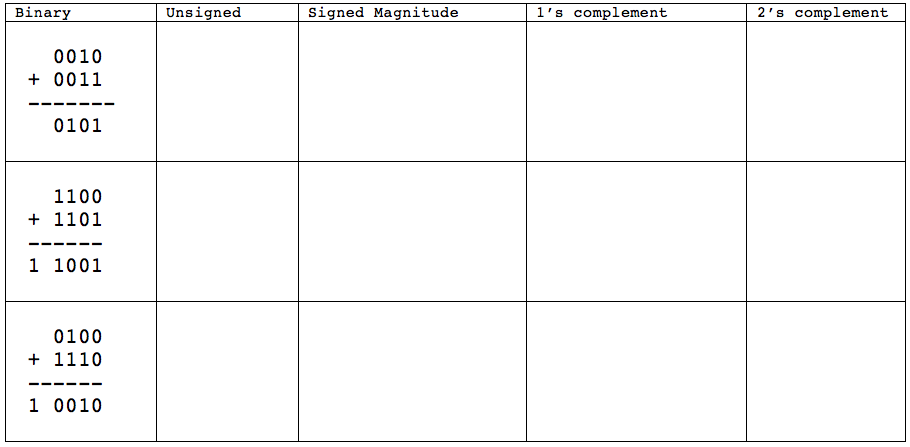
Exercise 5
- Perform the binary addition of the following decimal numbers using 2's complement, and assuming the numbers are 16-bit words
- (for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary)
23 - 100 = 23 - 23 = 100 - 23 =
Exercise 6
- A badly written software program is supposed to monitor and display the temperature recorded by a thermometer. This thermometer is used in chemical beaker. During an important experiment, the display outputs the following values:
- 56 59 70 81 99 110 -125
- What was the most likely true value of the last temperature recorded?
- (For reference, 125 in binary is 0111 1101, and -125 in 2's complement is 1000 0011.)
Solutions