Difference between revisions of "CSC212 Lab 13 2014"
(→Problem #4: 6 degrees of Separation) |
|||
| Line 76: | Line 76: | ||
=Problem #4: 6 degrees of Separation= | =Problem #4: 6 degrees of Separation= | ||
[[Image:KevinBacon6Degrees.jpg|200px|right]] | [[Image:KevinBacon6Degrees.jpg|200px|right]] | ||
| − | * Have you ever heard of Kevin Bacon's degrees of separation? The idea is explained [http://en.wikipedia.org/wiki/Six_Degrees_of_Kevin_Bacon | + | * Have you ever heard of Kevin Bacon's degrees of separation? The idea is explained [http://en.wikipedia.org/wiki/Six_Degrees_of_Kevin_Bacon in this Wikipedia page]. |
| + | |||
| + | * Interesting tidbit found on the same [http://en.wikipedia.org/wiki/Six_Degrees_of_Kevin_Bacon Wikipedia page]: | ||
| + | <blockquote> | ||
| + | While at the University of Virginia, Brett Tjaden created the Oracle of Bacon, a computer program that uses information on some '''800,000''' people from the Internet Movie Database (IMDb). The algorithm calculates "how good a center" an individual IMDb personality is, i.e. a weighted average of the degree of separation of all the people that link to that particular person. | ||
| + | </blockquote> | ||
| + | :There is an interesting ''graph shortest-path'' algorithm that you can try on the ''Oracle of Bacon'' [http://oracleofbacon.org/ Web site]. | ||
<br /> | <br /> | ||
* Assume that we take 100 Hollywood stars and record the connections that they have had during the past year. This generates a graph shown below. Each number represents a Hollywood star. The list of stars and numbers is available [[100 Top Hollywood Stars| here]]. | * Assume that we take 100 Hollywood stars and record the connections that they have had during the past year. This generates a graph shown below. Each number represents a Hollywood star. The list of stars and numbers is available [[100 Top Hollywood Stars| here]]. | ||
| Line 92: | Line 98: | ||
<br /> | <br /> | ||
| + | |||
=Problem #5= | =Problem #5= | ||
<br /> | <br /> | ||
Revision as of 17:16, 18 November 2014
--D. Thiebaut (talk) 11:19, 17 November 2014 (EST)
For Tuesday's lecture, do Problem #1 and Problem #2.
Contents
Problem #1: DFS
- Create a new program called Graph1.java and copy the code from this page.
- Implement the DFS function, with the main DFS function calling a recursive helper DFSRecurse function.
- Question 1
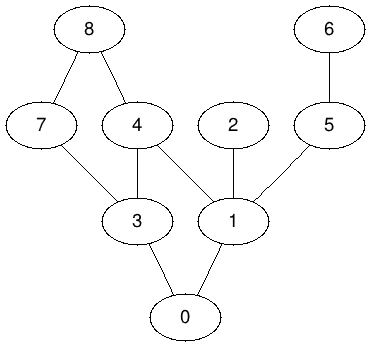
- Make your new DFS start with a vertex of your choice, and display all the vertices it visits. Below is an example of the output for G.DFS( 0 ).
DFS starting on 0: 0, 1, 2, 4, 3, 7, 8, 5, 6,
- Question 2
- Same question, but this time make DFS print the edges of the graph it visits. Below is an example of the output for G.DFS(0).
DFS starting on 0: visiting Edge (0)---(1) visiting Edge (1)---(2) visiting Edge (1)---(4) visiting Edge (4)---(3) visiting Edge (3)---(7) visiting Edge (7)---(8) visiting Edge (1)---(5) visiting Edge (5)---(6)
Problem #2: Connected Components
- A graph is connected if there is a path from any vertex to any other vertex in the graph.
- Create a new method called isConnected( ) that is based on DFS, and that returns true if the graph is connected, and false otherwise.
- The graph created by the init1() method is connected. You will need to add a new method called, say, init2() that initializes the graph with several disconnected components. (Hints: You can probably remove some edges from the graph generated by init1() to get a graph with several components!)
Problem #3: GraphViz & Dot
- Add a method to your graph that will print the graph in dot language, as we did with trees a while back.
- Here's the dot version of the graph generated by init1():
|
- You can test your dot definition at this URL: http://sandbox.kidstrythisathome.com/erdos/
Problem #4: 6 degrees of Separation
- Have you ever heard of Kevin Bacon's degrees of separation? The idea is explained in this Wikipedia page.
- Interesting tidbit found on the same Wikipedia page:
While at the University of Virginia, Brett Tjaden created the Oracle of Bacon, a computer program that uses information on some 800,000 people from the Internet Movie Database (IMDb). The algorithm calculates "how good a center" an individual IMDb personality is, i.e. a weighted average of the degree of separation of all the people that link to that particular person.
- There is an interesting graph shortest-path algorithm that you can try on the Oracle of Bacon Web site.
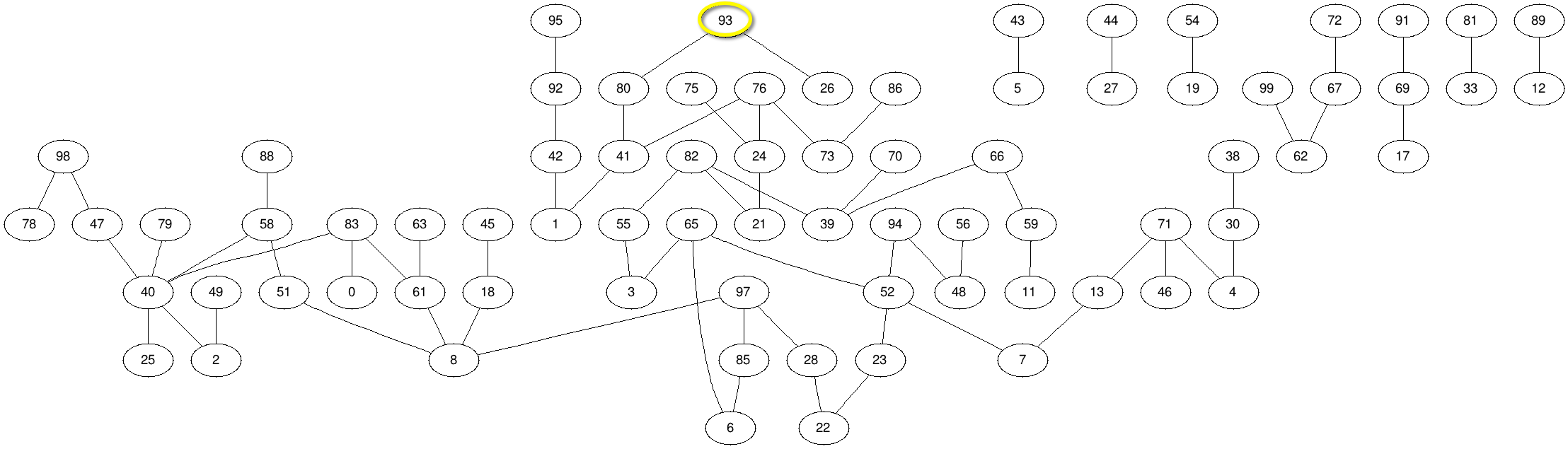
- Assume that we take 100 Hollywood stars and record the connections that they have had during the past year. This generates a graph shown below. Each number represents a Hollywood star. The list of stars and numbers is available here.
- Question 1
- Figure out a way to have your program output the Id of all the stars who are 1 degree away from Kevin Bacon.
- Question 2
- Make your program output the Ids of all the stars who are at most 4 degrees away from Kevin Bacon.
- Question 3
- Output all the Ids of the stars who are at an ∞ degree from Kevin Bacon.
Problem #5
To be provided later...