Difference between revisions of "CSC270 Homework 1"
(→Problem 1) |
|||
| Line 1: | Line 1: | ||
(c) --[[User:Thiebaut|D. Thiebaut]] 22:01, 28 January 2009 (UTC) | (c) --[[User:Thiebaut|D. Thiebaut]] 22:01, 28 January 2009 (UTC) | ||
<br /> | <br /> | ||
| − | [CSC270 | Back ] to Main Page | + | [[CSC270 | Back ]] to Main Page |
---- | ---- | ||
| Line 89: | Line 89: | ||
Be sure to explain why one assertion is true, or why it is false! | Be sure to explain why one assertion is true, or why it is false! | ||
| + | |||
| + | =Exercise #2= | ||
| + | |||
| + | Expand and simplify the function defined as f(a, b, c, d ) = Σ(0, 1, 2, 8, 10, 12, 13, 14, 15) | ||
| + | |||
| + | =Exercise #3= | ||
| + | |||
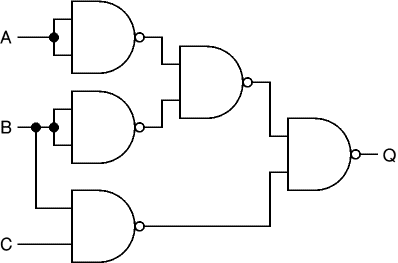
| + | [[Image:CSC270_gates3.gif | right]] | ||
| + | * What is the function f( A, B, C ) implemented by the circuit shown to the right, where the gates are NAND gates (an AND gate combined with a NOT gate on its output)? | ||
| + | * What is the '''minterm canonical form''' of f? | ||
Revision as of 17:22, 28 January 2009
(c) --D. Thiebaut 22:01, 28 January 2009 (UTC)
Back to Main Page
This assignment is due on Wednesday evening, at the beginning of Lab 2.
Problem 1
Assume that we define a Boolean Algebra where the two values possible are { α, β }, and where the operators are U, T, and NOT.
The U operator has the following truth table:
| x | y | x U y |
|---|---|---|
|
α |
α |
α |
|
α |
α |
α |
|
α |
α |
α |
|
α |
α |
β |
The T operator has the following truth table:
| x | y | x T y |
|---|---|---|
|
α |
α |
α |
|
α |
α |
β |
|
α |
α |
β |
|
α |
α |
β |
Which of these assertions is true?
- α is 1, β is 0, U is the AND operator, and T the OR operator
- α is 0, β is 1, U is the OR operator, and T is the AND operator
Be sure to explain why one assertion is true, or why it is false!
Exercise #2
Expand and simplify the function defined as f(a, b, c, d ) = Σ(0, 1, 2, 8, 10, 12, 13, 14, 15)
Exercise #3
- What is the function f( A, B, C ) implemented by the circuit shown to the right, where the gates are NAND gates (an AND gate combined with a NOT gate on its output)?
- What is the minterm canonical form of f?