Difference between revisions of "CSC270 Homework 3"
(New page: © D. Thiebaut, 2009 <br /> Back to Weekly Schedule ---- This assignment is due on Wednesday evening, at the beginning of Lab 4. =Exercise 1= Assume that we have a bo...) |
(→Exercise 2) |
||
| Line 20: | Line 20: | ||
<center> | <center> | ||
| − | [[CSC270_truthTable_abcde.png | 500px]] | + | [[Image:CSC270_truthTable_abcde.png | 500px]] |
</center> | </center> | ||
Revision as of 14:00, 11 February 2009
© D. Thiebaut, 2009
Back to Weekly Schedule
This assignment is due on Wednesday evening, at the beginning of Lab 4.
Exercise 1
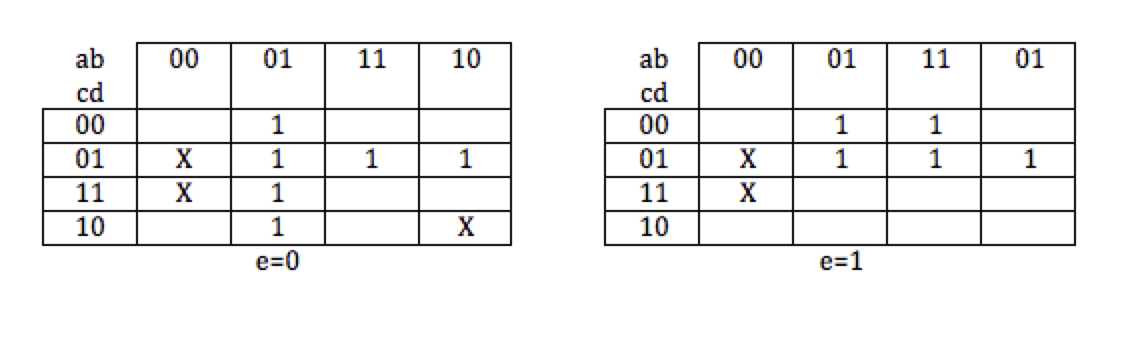
Assume that we have a boolean function f(a, b, c, d) = Σ( 5, 7, 15 ).
- What is its minimal form, as given by a Karnaugh map?
Assume furthermore we know that the the signals a and b are never both equal to 1 at the same time, and that c and d are never both equal to 00 at the same time. So, for example, the signals a, b, c, d will never be in the state 1 1 0 1, because that would require a, and b to be 1. Similarly, the condition a = 0, b=1, c=0, d=0 will never occur either, because c and d are 0 in this case.
How can we use this information to our advantage, as logic designers?