CSC270 Homework 3

© D. Thiebaut, 2009

Back to Weekly Schedule

---

This assignment is due on Thursday morning, after Rally Day, at 10:30 a.m. (office, or mailbox).

Exercise 1

Assume that we have a boolean function f(a, b, c, d) = Σ( 5, 7, 15 ).

What is its minimal form, as given by a Karnaugh map?

Assume furthermore we know that the the signals a and b are never both equal to 1 at the same time, and that c and d are never both equal to 00 at the same time. So, for example, the signals a, b, c, d will never be in the state 1 1 0 1, because that would require a, and b to be 1. Similarly, the condition a = 0, b=1, c=0, d=0 will never occur either, because c and d are 0 in this case.

How can we use this information to our advantage, as logic designers?

Exercise 2

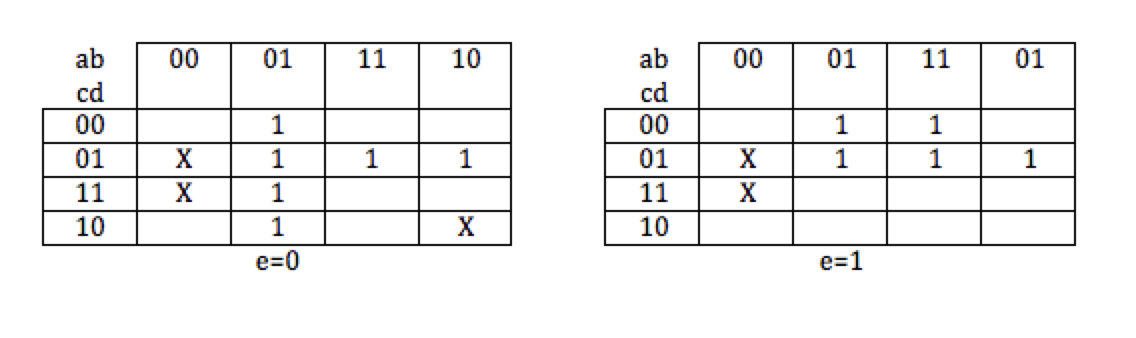
What is the simplified expression of the function g(a, b, c, d, e) expressed by the Karnaugh map above?

Exercise 3

Draw the logic diagram for the functions h() and k() below with 4-to-1 multiplexers:

• h( a, b, c, d ) = Σ( 0, 1, 2, 3, 4, 6, 12, 14 )

• k( a, b, c ) = Σ( 0, 1, 2, 3, 7 )

Exercise 4

Draw the logic diagram of the same functions with 8-to-1 multiplexers.

Exercise 5

Same question as for Exercise 3, but this time we know that minterms m5, m7, m12, and m13 correspond to don't care conditions for the function h(), and that minterm m6 is a don't care condition for function k().

Exercise 6

Implement a 16-to-1 multiplexer with only 4-to-1 multiplexers.

Exercise 7

Find the solution to the "Challenge #2 of the day" of Lab 3. You do not have to wire it up (although you are welcome to double check that your circuit works!).

You only have to implement the majority signal.

Explain how you derive your answer, and draw the logic diagram where you will show the 74LS42 as a 3-to-8 decoder with its active-low Enable and its 8 active-low outputs, and its connection to the other gates, all included in one integrated circuit.