CSC111 Lab 13 2015b

--D. Thiebaut (talk) 20:44, 6 December 2015 (EST)

---

Recognizing Palindromes

A palindrome is a sentence that can be read forward and backward. For example "Able was I ere I saw Elba." Another one: "A man, a plan, a canal: Panama."

For this lab you are asked to write a function that is given a list, and that returns True if the list is a "palindromic", that is, if the list of items is the same scanning forward and scanning it backward. Below are example of lists that are "palindromic":

• [ 1, 10, 1 ]
• [ "hello", "hello" ]
• [ 1, "hello", "hello", 1 ]
• [ 1, 2, 10, -1, 10, 2, 1 ]

First, with your partner, generate a some lists that are not palindromes, and see what makes them so, compared to the lists above.

Explore several ways our collection of minions would do the work. You would give the whole list to a minion, who would be doing a tiny bit of work, then reduce the list, and possibly pass it on to another minion, who would do the same amount of work, etc, until one minion gets a list that is small enough that it can decided if it is a palindrome or not.

Write a program called lab13_1.py that contains a main program that takes different lists and tests wether they are palindromic using your recursive function.

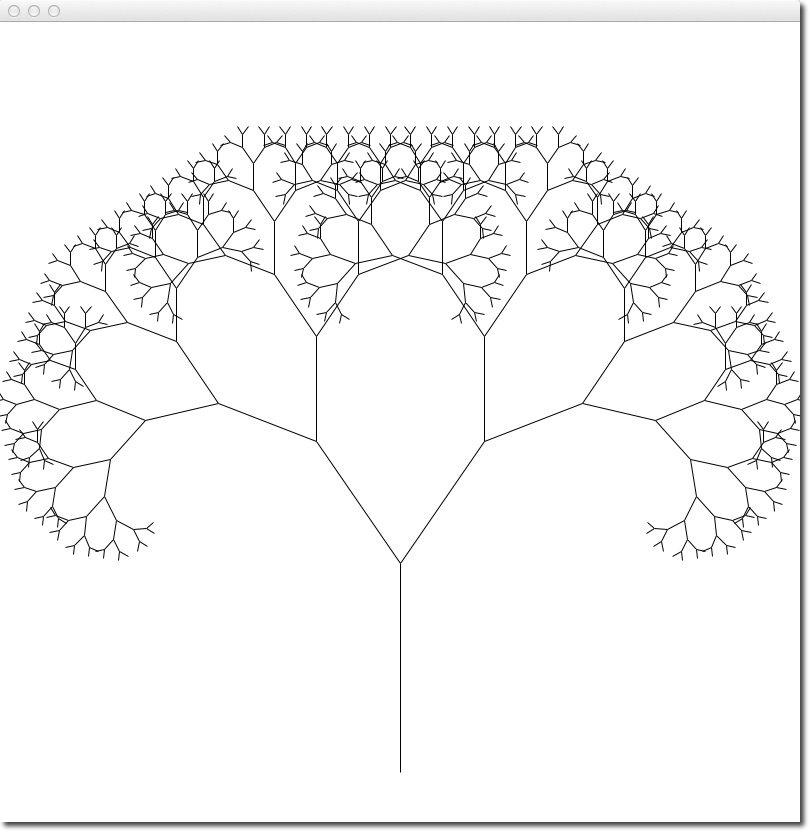
Fractal Trees

• This exercise is for you to explore recursion in the context of graphics.

• Create a new program with the code you'll find on this page, put it in the same directory where you store your graphics.py directory. You may want to call your program lab13_2.py.

• The program will generate a fractal tree. Fractals are self-similar objects: they look the same on a small scale as they do on a larger scale.

• Run the program first.
• Look at the code and see if you can figure out how the recursion works.
• To see how the different parameters influence the drawing of the fractal tree, modify the following parameters, one at a time, and give them different values:

theta

in the main program, change the angle theta which controls how much a branch will diverge from the direction of the branch that supports it. Try 0.4 first. Then try values between 0 and 0.8.

level of recursion

the main program passes 9 to the function as a starting level of recursion. Try passing smaller numbers first, then larger numbers (but less than 13 or so).

trunk_ratio

recursive function defines this as 0.29 and that represents the length of the trunk relative to its two branches. Try ratios between 0.1 (10%) and 0.9 (90%).