Difference between revisions of "CSC270 Lab 2 2016"
(→Nand Gates) |
(→Part 1) |
||
| Line 30: | Line 30: | ||
==Part 1== | ==Part 1== | ||
| + | <br /> | ||
Complete the circuit shown in Figure 1 by adding the part numbers of the circuits. Add this number inside the logic symbol, and also add the pin numbers on the inputs and outputs of the gates. Also, do not forget that each circuit requires power and ground. | Complete the circuit shown in Figure 1 by adding the part numbers of the circuits. Add this number inside the logic symbol, and also add the pin numbers on the inputs and outputs of the gates. Also, do not forget that each circuit requires power and ground. | ||
| Line 56: | Line 57: | ||
<br /> | <br /> | ||
| + | |||
==Part 2== | ==Part 2== | ||
<br /> | <br /> | ||
Revision as of 21:41, 3 February 2016
--D. Thiebaut (talk) 20:15, 3 February 2016 (EST)
Contents
Nand Gates
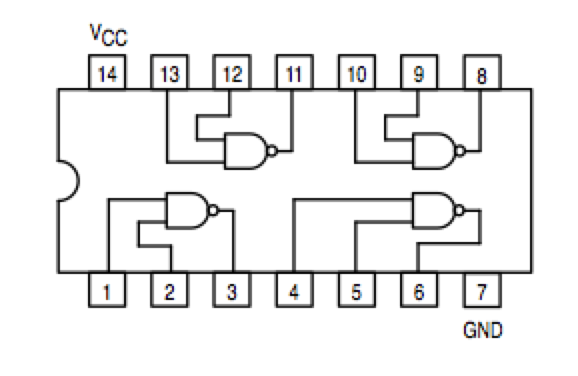
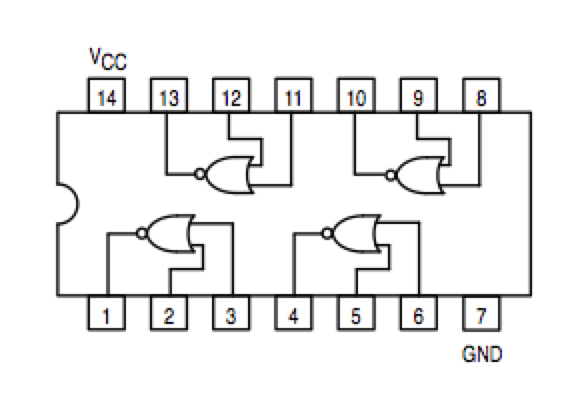
- Implement the 2-bit adder with NAND gates only. The figures below show the schematics of a NAND gate (and of a NOR gate, for completeness).
|
|
Hints: You may use the A, A', B, and B' logic switches if that can help you simplify your circuit. Less is more!
Decoder Circuit: the Do-It-Yourself version
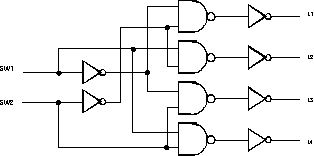
Part 1
Complete the circuit shown in Figure 1 by adding the part numbers of the circuits. Add this number inside the logic symbol, and also add the pin numbers on the inputs and outputs of the gates. Also, do not forget that each circuit requires power and ground.
- When you are done, implement the circuit on the breadboard section of your kit.
- Make sure you have turned off the power before you start wiring.
- Also, make sure that you connect the outputs of the inverters to the four logic indicators (LEDs). Verify your connections before you turn the power back on. Activate the two inputs and record the outputs in a truth table which you'll include in your report.
SW1 SW2 L4 L3 L2 L1 0 0 0 1 1 0 1 1
Because the inactive outputs are all set to zero, and the active one is set to 1, we refer to this type of circuit as a circuit with "active high" outputs.
Part 2
Now connect L1, L2, L3 and L4 to the input of the inverters rather than their output, and record the variation of L4, L3, L2 and L1 as a function of SW2 and SW1.
SW1 SW2 L4 L3 L2 L1 0 0 0 1 1 0 1 1
You now have the opposite behavior, where the inactive outputs are all 1 except for one that is set to 0. We refer to this type of circuit as a circuit with active-low outputs.
Most decoders work as the last circuit you just tested, rather than the one you first experimented with, although the first circuit had a more "intuitive" behavior.
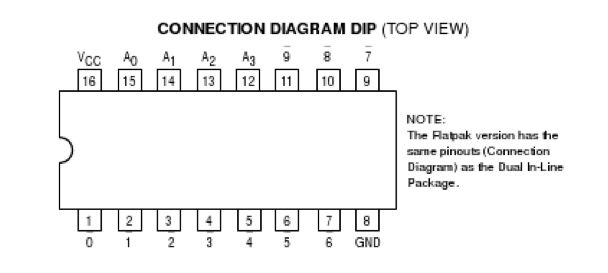
The 74LS42 Datasheet
Experiment #1
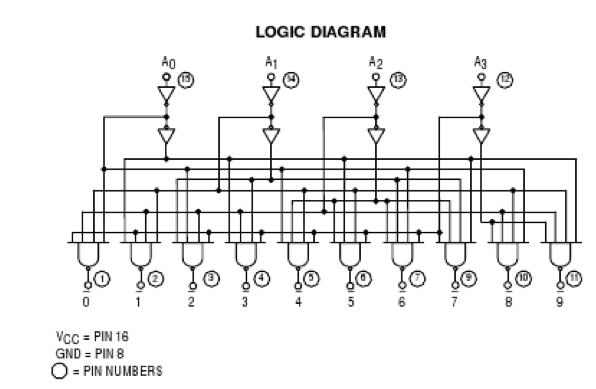
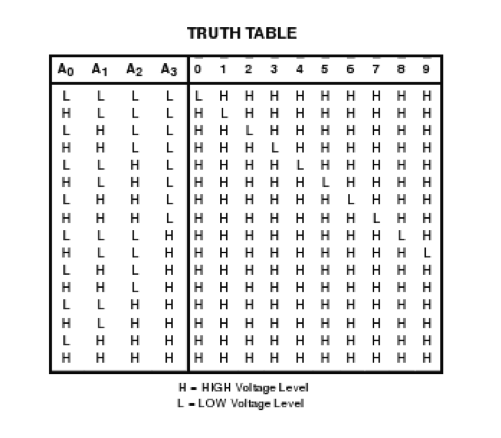
Study the 74LS42 data-sheet. Observe it carefully and figure out what kind of decoder it is:
- Question 1
- Is it a 3-to-8 decoder? A 4-to-16 decoder? If not, then what?
- Question 2
- Are the outputs active high or active low?
Using the schematics as your guide, design a 2-bit adder using this decoder, and as few other integrated circuits as possible. The fewer chips on your breadboard the better!
Experiment #3
We should have seen in class the basic concept of a multiplexer. (Wikipedia has a nice description of a multiplexer.)
Pick a simple design for a multiplexer, implement it (use Karnaugh maps!), and demonstrate that it works.