Difference between revisions of "CSC270 Homework 4 2016"
(→Problem 1) |
(→Problem 1) |
||
| Line 10: | Line 10: | ||
<br /> | <br /> | ||
[[Image:MuxExercise2.png|center|350px]] | [[Image:MuxExercise2.png|center|350px]] | ||
| + | <br /> | ||
| + | =Problem 2= | ||
| + | <br /> | ||
| + | Implement your two answers for Problem 1 in Python, and shown that your design is correct (although it might not be as minimal as required). | ||
| + | <br /> | ||
| + | Your Python code should have the following features: | ||
| + | * It must contain a header with your name(s), and a description of what it does | ||
| + | * It must contain a ''mux()'' function with 6 inputs (A, B, C, D, C1, C0), and returning one value (Y). | ||
| + | * It must generate the truth table for ''f'' and for ''g''. | ||
<br /> | <br /> | ||
Revision as of 10:54, 16 February 2016
--D. Thiebaut (talk) 10:50, 16 February 2016 (EST)
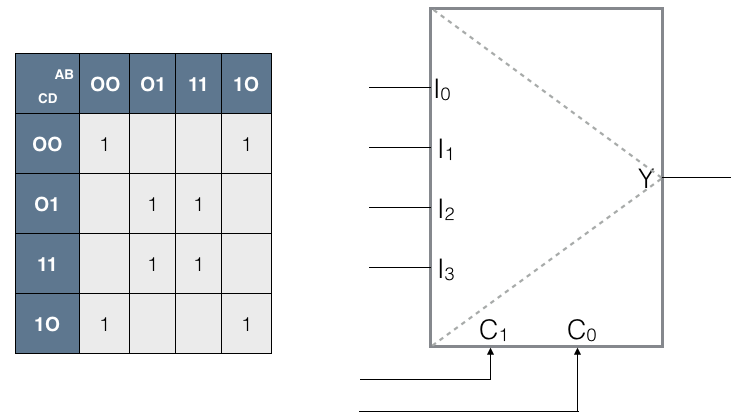
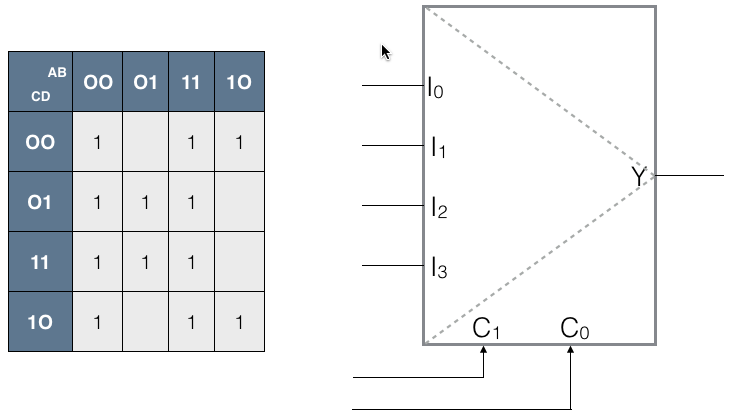
Problem 1
- Using as few additional gates as possible, implement the function f(A, B, C, D) whose Karnaugh map is shown below, on the left, using th e multiplexer shown on the right.
- Using as few additional gates as possible, implement the function g(A, B, C, D) whose Karnaugh map is shown below, on the left, using th e multiplexer shown on the right.
Problem 2
Implement your two answers for Problem 1 in Python, and shown that your design is correct (although it might not be as minimal as required).
Your Python code should have the following features:
- It must contain a header with your name(s), and a description of what it does
- It must contain a mux() function with 6 inputs (A, B, C, D, C1, C0), and returning one value (Y).
- It must generate the truth table for f and for g.