Difference between revisions of "CSC270 Homework 4 2016"
(→Problem 2) |
(→Problem 1) |
||
| Line 8: | Line 8: | ||
=Problem 1= | =Problem 1= | ||
<br /> | <br /> | ||
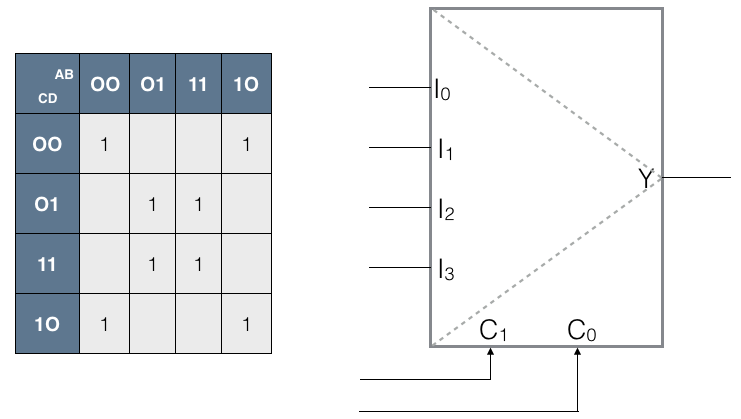
| − | * Using '''as few additional gates as possible''', implement the function ''f(A, B, C, D)'' whose Karnaugh map is shown below, on the left, using | + | * Using '''as few additional gates as possible''', implement the function ''f(A, B, C, D)'' whose Karnaugh map is shown below, on the left, using the multiplexer shown on the right. |
<br /> | <br /> | ||
[[Image:MuxExercise1.png|center|350px]] | [[Image:MuxExercise1.png|center|350px]] | ||
<br /> | <br /> | ||
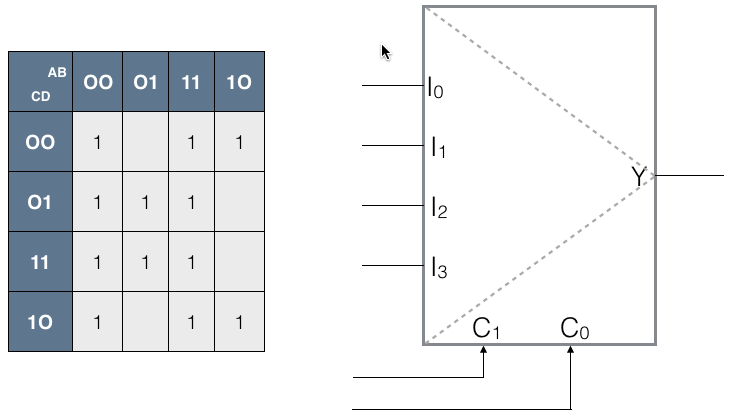
| − | * Using '''as few additional gates as possible''', implement the function ''g(A, B, C, D)'' whose Karnaugh map is shown below, on the left, using | + | * Using '''as few additional gates as possible''', implement the function ''g(A, B, C, D)'' whose Karnaugh map is shown below, on the left, using the multiplexer shown on the right. |
<br /> | <br /> | ||
[[Image:MuxExercise2.png|center|350px]] | [[Image:MuxExercise2.png|center|350px]] | ||
<br /> | <br /> | ||
| + | |||
=Problem 2= | =Problem 2= | ||
<br /> | <br /> | ||
Revision as of 15:40, 23 February 2016
--D. Thiebaut (talk) 10:50, 16 February 2016 (EST)
This assignment is due on 2/25/16 at 11:55 p.m. You need to submit a pdf on Moodle, in the Homework 4 section. You can work in pairs or individually.
Contents
Problem 1
- Using as few additional gates as possible, implement the function f(A, B, C, D) whose Karnaugh map is shown below, on the left, using the multiplexer shown on the right.
- Using as few additional gates as possible, implement the function g(A, B, C, D) whose Karnaugh map is shown below, on the left, using the multiplexer shown on the right.
Problem 2
Implement your two answers for Problem 1 in Python (or Java), and shown that your design is correct (although it might not be as minimal as required).
Your Python code should have the following features:
- It must contain a header with your name(s), and a description of what it does
- It must contain a mux() function with 6 inputs (A, B, C, D, C1, C0), and returning one value (Y).
- It must generate the truth table for f and for g.
Include the code and a copy of the output in your pdf. Please use a non-proportional font when displaying code and output: it makes it much easier for the reader to understand code quickly.
Problem 3
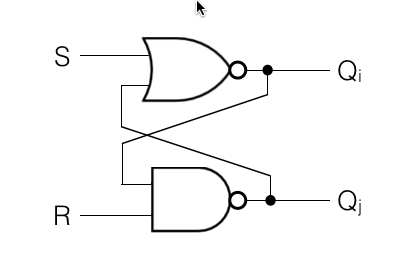
Is the circuit below a latch? Why or why not?
If you find out that it is a latch, you should be able to indicate:
- What are the inputs that are "passing" and putting the latch in a stable state.
- What input (S or R) must be activated (and how) to force a 1 on Qi
- What input (S or R) must be activated (and how) to force a 0 on Qi
Problem 4
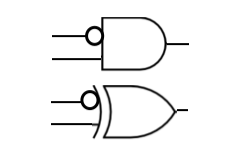
- Can a latch be created with the upper of the two circuits above (AND with one inverted input)? You can use as many of these special ANDs as you need.
- Same question about the lower circuit (XOR with one inverted input)? You can use as many of these special XORs as you need.
- Please explain carefully why it is possible to create a latch, or why it is not possible to create a latch with each one the circuits.