CSC103 2017: Instructor's Notes

--D. Thiebaut (talk) 15:27, 7 September 2017 (EDT)

---

CSC103 How Computers Work--Class Notes

...

Preface

This book presents material that I teach regularly in a half-semester course titles How Computers Work, in the department of computer science at Smith College. This course is intended for a general audience, and not specifically for computer science majors. Therefore you do not need any specific background to approach the material presented here. Furthermore, the material is self-contained, and you do not need to take the class to understand the material.

The goal of the course is to make students literate about the basic operations of a modern computer, and to cover some of the concepts and issues that are assumed to be understood by the general population, in particular concepts one will find in newspaper articles, such as that of the von Neumann bottleneck, or Moore's Law.

Understanding how computers work first requires observing that they are the physical implementation of rules of mathematics. So in the first part of this book we introduce simple concepts of logic, and explain how the binary system (where we only have 0 and 1 as digits to express numbers) works. We then explain how electronic switches, such as transistors, can be used to implement simple logic circuits which we call logic gates. Remarkably, these logic gates are all that is needed to perform arithmetic operations, such as addition or subtractions, on binary numbers.

This brings us to having a rough, though accurate, unerstanding of how simple hand-held calculators work. They are basically machines that translate decimal numbers into binary numbers, and carry these numbers through different paths through logic circuits to generate the sum, difference or multiplication

At this point, we figure out that an important part of computers and computing as to do with codes. A code is just a system where some symbols are used to represent other symbols. The simplest code we introduce is the one we use to pass from the world of logic where everything is either true or false to the world of binary numbers where digits are either 1 or 0. In this case the code we use is to say that the value true can also be represented by 1, and false by 0. Codes are extremely important in the computer world, as everything at the lowest level is really based on 1s and 0s, but we organize the information through coding to represent extremely complex and sophisticated systems.

Our next step is to see how we can use 1s and 0s to represent actions instead of data. For example, we can use 1 to represent the sum of two numbers, and 0 to represent the subtraction of the second from the first. In this case, if we write 10 1 11, we could mean that we want to add 10 to 11. In turn, writing 11 0 10 would mean subtracting 10 from 11. That is the basis for our exploration of machine language and assembly language. This is probably the most challenging chapter of this book. It requires a methodical approach to learning the material, and a good attention to details. We use a simple computer simulator to write simple, yet complex, assembly language programs that are the basis of all computer programs written today. Your phone, tablet, or laptop all run applications (apps) that are large collection of assembly language instructions.

Because assembly language deals with operations that happen at the tiniest of levels in a computer, it referred to as a low-level language. When engineers write apps for data phones, tablets or laptops, they use languages that allow them to deal with much more complex structures at once. These languages are called high-level languages. Learning how computers work also requires understanding how to control them using some of the tools routinely used by engineers. We introduce Processing as an example of one such language. Processing was created by Ben Fry and Casey Reas at the MIT Media Labs. Their goal was to create a language for artists that would allow one to easily and quickly create artistic compositions, either as static images, music, or videos. The result is Processing; it provides an environment that is user-friendly and uses a simplified version of Java that artists can use to create sketches (Processing programs are called sketches). The Exhibition page of the Processing Web site presents often interesting and sometimes stunning sketches submitted by users.

Introduction

Current Computer Design is the Result of an Evolutionary Process

In this course we are going to look at the computer as a tool, as the result of technological experiments that have crystalized currently on a particular design, the von Neumann architecture, on a particular source of energy, electricity, on a particular fabrication technology, silicon transistors, and a particular information representation, the binary system, but any of these could have been different, depending on many factors. In fact, in the next ten or twenty years, one of more of these fundamental parts that make today's computers could change.

Steamboy, a steampunk Japanese animé by director Katsuhiro Ohtomo (who also directed Akira) is interesting in more than the story of a little boy who is searching for his father, a scientist who has discovered a secret method for controlling high pressured steam. What is interesting is that the movie is science fiction taking place not in the future, but in middle of the 19th century, in a world where steam progress and steam machines are much more advanced than they actually were at that time. One can imagine that some events, and some discoveries where made in the world portrayed in the animated film, and that technology evolved in quite a different direction, bringing with it new machines, either steam-controlled tank-like vehicles, or ships, or flying machines.

For computers, we can make the same observation. The reason our laptops today are designed the way they are is really the result of happy accidents in some ways. The way computers are designed, for example, with one processor (more on multi-core processors later), a system of busses, and memory where both data and programs reside side-by-side hasn't changed since John von Neumann wrote his (incomplete and never officially published) First Draft of a Report on the EDVAC, article, in June of 1945. One can argue that if von Neumann hadn't written this report, we may have followed somebody else's brilliant idea for putting together a machine working with electricity, where information is stored and operated on in binary form. Our laptop today could be using a different architecture, and programming them might be a totally different type of problem solving.

Antikythera Mechanism, photo taken by Tilemahos Efthimiadis, National Archaeological Museum, Athens, Greece., taken from commons.wikimedia.org, July 28 2014. Released under the Creative Commons Attribution 2.0 Generic license.

For computers were not always electrical machines. Initially they were mechanical machines. The abacus, which appeared several millennia B.C. was a counting machine made of wood. The Antikythera mechanism, is currently regarded as the first mechanical machine for computing astronomical calculations. Mechanical as well, the important machine in the history of computers is Babbage's Difference Engine. This one was made of gears and shafts, with a crank at the top, and was a general purpose machine. Interestingly, this machine has given us an expression we still use with modern electronic computers: we still hear programmers refer to "cranking out" the results, even though the crank is long gone.

The same is true of silicon transistors powered by electricity. Silicon is the material of choice for electronic microprocessor circuits as well as semiconductor circuits we find in today's computers. Its appeal lies in its property of being able to either conduct and not conduct electricity, depending on a signal it receives which is also electrical. Silicon allows us to create electrical switches that are very fast, very small, and consume very little power. But because we are very good at creating semiconductor in silicon, it doesn't mean that it is the substrate of choice. Researchers have shown that complex computation could also be done using DNA, in vials. Think about it: no electricity there; just many vials with solutions containing DNA molecules, a huge number of them, that are induced to code all possible combinations of a particular sequence, such that one of the combinations is the solution to the problem to solve. DNA computing is a form of parallel computation where many different solutions are computed at the same time, in parallel, using DNA molecules. One last example for computation that is not performed in silicon by traveling electrons can be found in optical computing. The idea behind this concept (we really do not have optical computers yet, just isolated experiments showing its potential) is that electrons are replaced with photons, and these photons, which are faster than electrons, but much harder to control.

So, in summary, we start seeing that computing, at least the medium chosen for where the computation takes place can be varied, and does not have to be silicon. Indeed, there exist many examples of computational devices that do not use electronics in silicon and can perform quite complex computation. In consequence, we should also be ready to imagine that new computers in ten, twenty or thirty years will not use semiconductors made of silicon, and may not use electrons to carry information that is controlled by transistors. In fact, it is highly probable that they won't.

While the technology used in creating today's computer is the result of an evolution and choices driven by economic factors and scientific discoveries, among others, one thing we can be sure of is that whatever computing machine we devise and use to perform calculations, that machine will have to use rules of mathematics. It does not matter what technology we use to compute 2 + 2. The computer must follow strict rules and implement basic mathematical rules in the way it treats information.

You may think that Math may be necessary only for programs that, say, display a mathematical curve on the screen, or maintain a spreadsheet of numbers representing somebody's income tax return, but Math might probably not be involved in a video game where we control an avatar who moves in a virtual world. Or that the computer inside a modern data phone is probably not using laws of Mathematics for the great majority of what we du with it during the day. This couldn't be further from the truth. Figuring out where a tree should appear on the screen as our avatar is moving in its virtual space requires applying basic geometry in three dimensions: the tree is at a corner of a triangle formed by the tree, the avatar, and the eye of the virtual camera showing you the image of this virtual world. Our phone's ability to pin point its location as we're sitting in a café sipping on a bubble tea, requires geometry again, a program deep in the phone figuring out how far we are from various signal towers for which the phone knows the exact location, and using triangulation techniques to find our place in relationship to them.

So computers, because they need to perform mathematical operations constantly, must know the rules of mathematics. Whatever they do, they must do it in a way that maintains mathematical integrity. They must also be consistent and predictable. 2 + 2 computed today should yield the same result tomorrow, independent of which computer we use. This is one reason we send mathematical equations onboard space probes that are sent to explore the universe outside our solar system. If there is intelligent life out there, and if it finds our probe, and if it looks inside, it will find math. And the math for this intelligent life will behave the same as math for us. Mathematics, its formulas, its rules, are universal.

But technological processes are not. So computers can be designed using very different technologies, but whatever form they take, they will follow the rules of math when performing computations.

In our present case, the major influence on the way our computers are build is the fact that we are using electricity as the source of power, and that we're using fast moving electrons to represent, or code information. Electrons are cheap. They are also very fast, moving at approximately 3/4 the speed of light in wires. We know how to generate them cheaply (power source), how to control them easily (with switches), and how to transfer them (over electrical wires). These properties were the reason for the development of the first vacuum tube computer by Atanasoff in 1939.

The choice of using electricity has influenced greatly a fundamental way in which modern computers work. They all use the binary system at the lowest level. Because electricity can be turned ON or OFF with a switch, it was only logical that these two states would be used to represent information. ON and OFF. 0 and 1. True and False. But if we can represent two different states, two different levels of information, can we represent other than 0 or 1? Say 257? Can we also organize electrical circuitry that can perform the addition of two numbers? The answer is Yes; using the binary numbering system.

Binary System

This section is an overview of the binary system. Better sources of information can be found on this subject, including this one from the University of Vermont.

To better understand the binary system, we'll refresh our memory about the way our decimal system works, figure out what rules we use to operate in decimal, and carry them over to binary.

First, we'll need to define a new term. The base of a system is the number of digits used in the system. Decimal: base 10: we have 10 digits to write numbers with: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

In binary, the base is 2; we have only two digits to write numbers with: 0, and 1.

Counting in Decimal

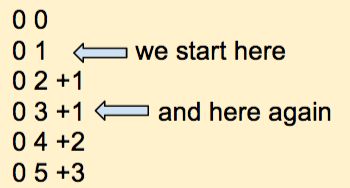
Let's now count in decimal and go slowly, figuring out how we come up with the numbers.

That's the first positive number. Instead of just 1 zero, we pad the number with leading zeros so that the number has 3 digits. This will help us understand better the rule we're so good at using that we have forgotten it!

Let's continue:

Ok, now an important point in the counting process. We have written all 10 digits in the right-most position of our number. Because we could increment this digit, we didn't have to change the digits on the left. Now that we have reached 9, we need to roll over the list of digits. We have to go from 9 back to 0. Because of this roll-over, we have to increment (that means adding 1) the digit that is directly to the left of the one rolling over.

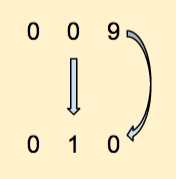
Let's continue:

Notice that after a while we reach 019. The right-most digit has to roll over again, which makes it become 0, and the digit to its left must be incremented by 1. From 1 it becomes 2, and we get 020.

At some point, applying this rule we reach 099. Let's just apply our simple rule: the right most digit must roll over, so it becomes 0, and the digit to its left increments by 1. Because this second digit is also 9 it, too, must roll over and become 0. And because the 2nd digit rolls over, then the third digit increments by 1. We get 100. Does that make sense? We are so good at doing this by heart without thinking of the process we use that sometimes it is confusing to deconstruct such knowledge.

So let's remember this simple rule; it applies to counting in all number systems, whether they are in base 10 or some other base:

When counting, we always increment the right-most digit by 1. When this digit must roll-over back to 0, we do so, and increment the digit to its left. If this one rolls over to 0 as well, then we do so and increment the digit to its left, and so on.

Counting in Binary

Let's now count in base 2, in binary. This time our "internal" table contains only 2 digits: 0, 1. So, whatever we do, we can only use 0 and 1 to write numbers. And the list of numbers we use and from which we'll "roll-over" is simply: 0, 1.

Good start! That's zero. It doesn't matter that we used 5 0s to write it. Leading 0s do not change the value of numbers, in any base whatsoever. We use them here because they help see the process better.

We apply the rule: modify the right-most digit and increment it. 0 becomes 1. No rolling over.

Good again! One more time: we increment the rightmost digit, but because we have reached the end of the available digits, we must roll over. The right-most digit becomes 0, and we increment its left neighbor:

Once more: increment the right-most digit: this time it doesn't roll-over, and we do not modify anything else.

One more time: increment the right-most digit: it rolls over and becomes 0. We have to increment its neighbor to the left, which also rolls over and becomes 0, and forces us to increment its neighbor to the left, the middle digit, which becomes 1:

Let's pick up the pace:

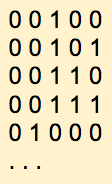
And so on. That's basically it for counting in binary.

Let's put the numbers we've generated in decimal and in binary next to each other:

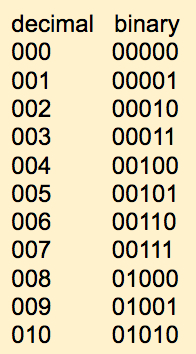
Exercise

How would we count in base 3? The answer is that we just need to modify our table of available digits to be 0, 1, 2, and apply the rule we developed above. Here is a start:

0000
0001
0002
0010     (2 rolls over to 0, therefore we increment its left neighbor by 1)
...

Does that make sense? Continue and write all the numbers until you reach 1000, in base 3.

Evaluating Binary Numbers

What is the decimal equivalent of the binary number 11001 in decimal? To find out, we return to the decimal system and see how we evaluate, or find the value represented by a decimal number. For example:

1247

represents one thousand two hundred forty seven, and we are very good at imagining how large a quantity that is. For example, if you were told that you were to carry 1247 pennies in a bag, you get a sense of how heavy that bag would be.

The value of 1247 is 1 x 1000 + 2 * 100 + 4 * 10 + 7 * 1. The 1000, 100, 10, and 1 factors represent different powers of the base, 10. We can also rewrite it as

     1247 = 1 x 103 + 2 x 102 + 4 x 101 + 7 x 100
 
             = 1 x 1000 + 2 x 100 + 4 x 10 + 7 x 1
             = 1247

So the rule here is that to find the value or weight of a number written in a particular base is to multiply each digit by the base raised to increasing powers, starting with the power 0 for the rightmost digit.

Let's try that for the binary number 11001. The base is 2 in this case, so the value is computed as:

   11001 = 1 x 24 + 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 
 
         = 1 x 16 + 1 x 8 + 0 x 4 + 0 x 2 + 1 x 1
  
         = 16 + 8 + 0 + 0 + 1
   
         = 25 in decimal

Binary Arithmetic

So far, we can count in binary, and we now how to find the decimal value of a binary number. But could we perform arithmetic with binary numbers? If we can, then we're that much closer to figure out how to build a computer that can perform computation. Remember, that's our objective in this chapter: try to understand how something build with electronic circuits that operate with electricity that can be turned on or off can be used to perform the addition of numbers. If we can add numbers, surely we can also multiply, subtract, divide, and we have an electronic calculator.

Once again we start with decimal. Base 10. Only 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

Let's add 133 to 385

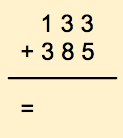
It's tempting to just go ahead and find the answer, isn't it? Instead let's do it a different way and concentrate only on 3 + 5. For this we write down the list of all available digits, in increasing order of weights. For the purpose of this section, we'll call this list of digits the table of available digits.

The result is 8.

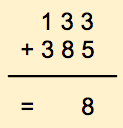
We move on the next column and add 3 + 8. Using our table of digits, this is what we get:

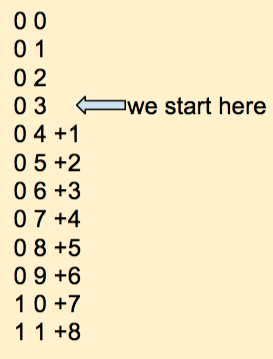
Here we had to roll over our list of available digits. We know the rule! When we roll over we add 1 to the digit on the left. In this case the digits on the left. We'll put this new digit (red) above the third column of numbers as follows:

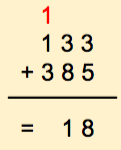
So now we have 3 numbers to add: 1, 1 and 3:

The result:

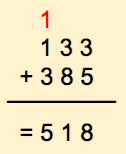
If we find ourselves in the case where adding the leftmost digits creates a roll-over, we simply pad the numbers with 0 and we find the logic answer.

So we have a new rule to add numbers in decimal, but actually one that should hold with any base system:

We align the numbers one above the other. We start with rightmost column of digits. We take the first digit in the column and start with it in the table of digits. We then go down the table a number of steps equivalent to the digit we have to add to that number. Which ever digit we end up on in the table that's the digit we put down as the answer. If we have to roll-over when we go down the table, then we put a 1 in the column to the left. We then apply the rule to the next column of digits to the left, until we have processed all the columns.

Ready to try this in binary? Let's take two binary numbers and add them:

      1010011
   +  0010110
  ------------

Our table of digits is now simpler:

     0
     1

Here we start with the rightmost column, start at 1 in the table and go down by 0. The result is 1. We don't move in the table:

      1010011
   +  0010110
  ------------
            1

Done with the rightmost column. We move to the next column and add 1 to 1 (don't think too fast and assume it's 2! 2 does not exist in our table of digits!)

     0
     1    <---- we start here, and go down by 1
  ------
   1 0    +1

We had to roll-over in the table. Therefore we take a carry of 1 and add it to the column on the left.

      	   1
      1010011
   +  0010110
  ------------
      	   01

Continuing this we finally get

      1010011
   +  0010110
  ------------
      1101001

Let's verify that this is the correct answer. 1010011, in decimal is 64 + 16 + 2 + 1 = 83. 10110 is 16 + 4 + 2 = 22. 83 + 22 is 105. There 1101001 must represent 105. Double check: 1101001 is 64 + 32 + 8+ 1 which, indeed is 105.

So, in summary, it doesn't matter if we are limited to having only two digits, we can still count, represent numbers, and do arithmetic.

Summary of Where we Are

Let's summarize what we know and what we're after. We know that electricity is cheap, easy to control, a great source of power, and that we can easily build switches that can control voltages over wire. We know that we can create a code associating 1 to electricity being ON and 0 to electricity being OFF in a wire. So electricity can be used to represent the numbers 0 and 1.

Furthermore, we know that a system where we only have two digits is called the binary system, and that this system is mathematically complete, allowing us to do everything we can do in decimal (we have concentrated in the previous discussion to just counting and adding, but we can do everything else the same).

So the question now for engineers around the middle of the 20th century was how to build electrical/electronic circuits that would perform arithmetic.

The answer to this problem is provided by two giants of computer science, George Boole , and Claude Shannon who lived at very different times, but provided two complementary parts of the solution. Boole (1815-1864) defined the Boolean algebra, a logic system that borrowed from philosophy and from mathematics, where assertions (mathematicians say variables) can only be true' or false, and where assertions can be combined by any combination of three conjunctions (which mathematicians call operators): and, or and not.

Many years later, Claude Shannon (1916-2001) showed in his Master's thesis that arithmetic operations on binary numbers could be performed using Boole's logic operators. In essence, if we map True and False to 1 and 0, adding two binary numbers can be done using logic operations.

We'll now look at Boole and Shannon separately.

Boole and the Boolean Algebra

Boole's contribution is a major one in the history of computers. In the 1840s, he conceived of a mathematical world where there would be only two symbols, two values, and three operations that could be performed with them, and he proved that such a system could exhibit the same rules exhibited by an algebra. The two values used by Boole's algebra are True and False, or T and F, and the operators are and, or and not. Boole was in fact interested in logic, and expressing combinations of statements that can either be true or false, and figuring out whether mathematics could be helpful in formulating a logic system where we could express any logical expression containing multiple simple statements that could be either true or false.

While this seems something more interesting to philosophers than mathematicians or engineers, this system is the foundation of modern electronic computers.

Each of the boolean operators can be expressed by a truth table.

a	b	a and b
F	F	F
F	T	F
T	F	F
T	T	T

The table above is the truth table for the and logical operator. It says that if the statement a is true, and if b is false, then the and operator makes the result of a and b false. Only if both statements are true will the result of and-ing them together be true. This is still pretty abstract. Let's see if we can make this clearer. Assume that a is the statement Today is Monday, and that b is the statement The time is 9:00 a.m., and that you want to be reminded every Monday at 9:00 a.m. to go to Ford Hall to take a particular class. So we can define the alarm signal that reminds you to be a and b. The alarm will ring only when the day is Monday, and the time is 9:00 a.m. At 9:00 a.m. on Tuesdays nothing will happen, because at that particular time a is false, and b is true, but the and operator is extremely strick and will not generate true if only one of its operands is true.

The truth table for the or operator is the following:

a	b	a or b
F	F	F
F	T	T
T	F	T
T	T	T

Let's keep our alarm example and think of how to program an alarm so that we can spend the morning in bed and not get up early on Saturdays and Sundays. We could have Statement a be "Today is Saturday", and Statement b be "Today is Sunday". The boolean expression that will allow us to enjoy a morning in bed on weekends is a or b. We can make our decision by saying: "if a or b, we can stay in bed." On Saturdays, a is true, and the whole expression is true. On Sundays, b is true, and we can also stay in bed. On any other day, both a and b are false, and or-ing them together yields false, and we'd better get up early!

This all should start sounding familiar and "logical" by now. In fact, we use the same logic when searching for information on the Web, or at the library. For example, assume we are interested in searching for information about how to write a class construct in the language Python. You could try to enter Python class, which most search engine will internally translate as a search for "Python and class". Very likely you might find that the results include references to python the animal, not the programming language. So to prevent this from happening we can specify our search as python and class and (not snake).

Back to the alarm example. Assume that we have the same a and b boolean variables as previously, one that is true on Saturdays only and one that is true on Sundays only. How could we make this alarm go off for any weekday and not on weekends? We could simply say that we want the opposite of the alarm we had to see if we can stay in bed on weekends. So that would be not ( a or b ).

For completeness we should show the truth table for the not operator. It's pretty straightforward, and shown below:

a	not a
F	T
T	F

When a is true, not a is false, and conversely.

An Example and Exercise

Assume we want to build a logical machine that can use the logical operators and, or and not to help us buy ice cream for a friend. The friend in question has very specific taste, and likes ice cream with chocolate in it, ice cream with fruit in it, but not Haagen Dazs ice cream. This example and exercise demonstrate how we can build such a "machine".

D. Thiebaut, Ice Cream, 2014, Released under the Creative Commons Attribution 2.0 Generic license.

We can devise three boolean variables that can be true of false depending on three properties of a container of ice cream: choc, fruit, and HG. choc is true if the ice cream contains some chocolate. fruit is true if the ice cream contains fruits, and HG is true if the ice cream is from Haagen Dazs. A boolean function, or expression, we're going to call it isgood, containing choc, fruit, and HG that turns true whenever the ice cream is one our friend will like would be this:

isgood = ( choc or fruit ) and ( not HG )

Any ice cream container for which choc or fruit is true, and which is not HG will match our friend's taste.

We could represent this boolean function with a truth table as well.

choc	fruit	HG	choc or fruit	not HG	( choc or fruit ) and ( not HG )
F	F	F	F	T	F
F	F	T	F	F	F
F	T	F	T	T	T
F	T	T	T	F	F
T	F	F	T	T	T
T	F	T	T	F	F
T	T	F	T	T	T
T	T	T	T	F	F

The important parts of the table above are the first 3 columns and the last one. The first 3 columns list all the possibilities of having three boolean variables take all possible values of true and false. That corresponds to 2 x 2 x 2 = 8 rows. Let's take Row 4. It corresponds to the case choc = false, fruit = true, and HG = true. The fourth column shows the result of or-ing choc and fruit. Looking at the truth table for or above, we see that the result of false with true is true. Hence the T on the fourth row, fourth column. Column 5 contains not HG. Since HG is true on Row 4, then not HG is false. The sixth column represent the and of Column 4 with Column 5. If we and true and false, the truth table for and says the result is false. Hence that particular ice cream would not be good for our friend. That makes sense, our friend said no ice cream from Haagen Dazs, and the one with just picked does.

Below are some questions for you to figure out:

Question 1

Which row of the table would correspond to a container of Ben and Jerry's vanilla ice cream? Would our friend like it?

Question 2

How about a container of Ben and Jerry's strawberry chocolate ice cream?

Question 3

Assume that our friend has a younger brother with a different boolean equation for ice cream. His equation is ( (not choc) and fruit) and ( HG or ( not HG ) ). Give an example of several ice cream flavors and makers of ice cream the young brother will like.

Question 4 (challenging)

Can you find an ice cream flavor and maker that both our friend and his/her younger brother will like?

Shannon's MIT Master's Thesis: the missing link

We are now coming to Shannon, who's influence on the field of computer science is quite remarkable, and whose contribution of possibly greatest influence was his Master's thesis at MIT, written in 1948.

Shannon knew of the need for calculators (human beings or machines) around the time of the second world-war, (the need was particularly great for machines that would compute tables of possible trajectories for shells fired from canons). He also knew of efforts by various groups in universities to build calculating machines using electricity and relays, and also of early experiments with vacuum tubes (which later replaced the relays). Because the machines used electricity and switches, the binary system with only two values, 0 and 1 was an appealing system to consider and exploit. But there was still an engineering gap in figuring out how to create circuits that would perform arithmetic operations on binary numbers in an efficient way.

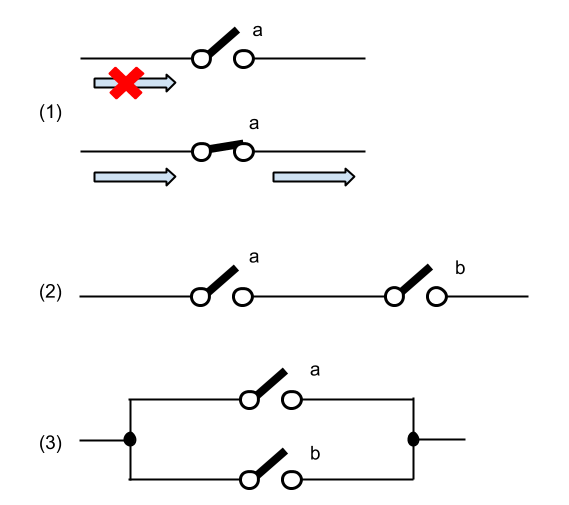
Also known at the time was the fact that Boolean logic was easy to implement with electrical systems. For example, creating a code system where a switch can represent the values of True or False is easy, as illustrated in the figure below, in the first (1) panel.

AND OR gates with switches. D. Thiebaut, 2014, Released under the Creative Commons Attribution 2.0 Generic license.

The black lines represent electrical wires carrying an electrical current. The two circles with an oblique bar represent an electrical switch, that can be ON or OFF. In the figure it is represented in the OFF position. In this position, no current can flow. When the oblique bar, which is a metalic object is brought down to touch the second white circle, it makes contact with the wire on the right, and the current can flow through the switch. In this case we can say that the OFF position of the switch represents the value False, and the ON position of the switch represents the value True, and the switch represents a boolean variable. If it is True, it lets current go through the circuit, and the presence of current will indicate a True condition. If the switch's status is False, no current can go through it, and the absence of current will mean False.

If we put two switches one after the other, as in Panel (2) of the same figure, we see that the current can flow through only if both switches are True. So putting switches in series corresponds to creating an and circuit. The current will flow through the and circuit is Switch a is True, and if Switch b is True. If either one of them is False, no current flows through. You can verify with the truth table for the Boolean And function above that this is indeed the behavior of a boolean and operator. Verify for yourself that the third circuit in the figure implements a boolean or operator. The circuit lets current go through if Switch a is True or if Switch b is True.

In his thesis, Shannon presented the missing link, the bridge that would allow electrical/electronic computers to perform arithmetic computation. He demonstrated that if one were to map True and False values to 1 and 0 of the binary system, then the rules of arithmetic because logic rules. That mean adding two integers because a problem in logic, where assertions are either true or false.

Let's see how this actually works out. Remember the section above when we added two binary numbers together? Let's just concentrate on the bit that is the rightmost bit of both numbers (in computer science we refere to this bit as the least significant bit). If we are adding two bits together, and if both of them can be either 0 or 1, then we have 4 possible possibilities:

    0          0          1          1
  + 0        + 1        + 0        + 1
  ----       ----       ----       ----

Using the rules we created above for adding two bits together, we get the following results:

    0          0          1          1
  + 0        + 1        + 0        + 1
  ----       ----       ----       ----
    0          1          1        1 0

Let's take another step which, although it doesn't seem necessary, is absolutely essential. You notice that the last addition generates a carry, and the result is 10. We get two bits. Let's add a leading 0 to the other three resulting bits

    0          0          1          1   <--- a
  + 0        + 1        + 0        + 1   <--- b
  ----       ----       ----       ----
  0 0        0 1        0 1        1 0   <--- S
                                     |  
                                     +---- C

Let's call the first bit a, the second bit b, the sum bit S, and the extra bit that we just added C (for carry). Let's show the same information we have in the four above additions into a table, similar to the truth tables we used before where we were discussing boolean algebra.

a	b	C	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Do you recognize anything? Anything looking familiar? If not, let's use a code, and change all the 1s for Ts and all the 0s for Fs, and split the table in two:

a	b	C
F	F	F
F	T	F
T	F	F
T	T	T

and

a	b	S
F	F	F
F	T	T
T	F	T
T	T	F

Now, if we observe the first table, we should recognize the table for the and operator! So it is true: arithmetic on bits can actually be done as a logic operation. But is it true of the S bit? We do not recognize the truth table of a known operator. But remember the ice cream example; we probably come up with a logic expression that matches this table. An easy way to come up with this expression is to express it in English first and then translate it into a logic expression:

S is true in two cases: when a is true and b is false, or when a is false and b is true.

or

S = ( a and not b ) or ( not a and b )

As an exercise you can generate the truth table for all the terms in this expression and see if their combinational expression here is the same as S.

So, here we are with our premises about our current computers and why they work. We have answered important questions and made significant discoveries, which we summarize below

Discoveries

• Computers use electricity as a source of power, and use flows of electrons (electric currents) to convey information.
• Switches are used to control the flow of electrons, creating a system of two values based on whether the flow is ON or OFF.
• While the binary system uses only two digits it is just as powerful as the system of decimal numbers, allowing one to count, add, and do arithmetic operations with binary numbers.
• The boolean algebra is a system which also sports two values, true and false, and logical operators and well defined properties.
• Logic operator are easy to generate with electronic switches
• Arithmetic operations in binary can be expressed using the operators of the boolean algebra.

Logic Gates

Now that Shannon had shown that computing operations (such as arithmetic) could be done with logic, engineers started creating special electronic circuits that implemented the basic logic operations: AND, OR, and NOT. Because the logical operators are universal, i.e. you can create any boolean function by combining the right logical operators with boolean variables, then these special circuits became universal circuits. We have a special name for them: gates.

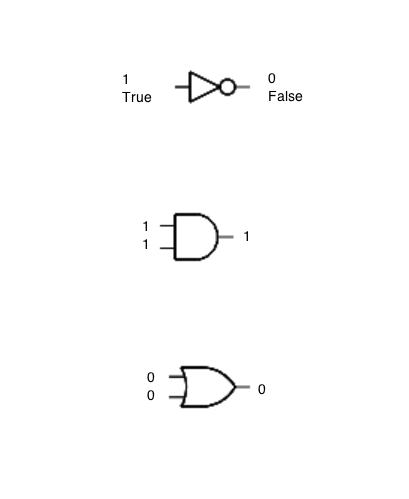
A gate is simply an electronic circuit that uses electricity and implements a logic function. Instead of using True or False, though, we find it easier to replace True by 1 and False by 0.

Inverter, And, and Or gates. D. Thiebaut, 2014, Released under the Creative Commons Attribution 2.0 Generic license.

The gates have the same truth table as the logic operators they represent, except now we'll use 1s and 0s instead of T or F to represent them. For example, below is the truth table for the OR gate:

The truth table for the OR gate is the following:

a	b	a or b
0	0	0
0	1	1
1	0	1
1	1	1

The truth table for the AND gate:

a	b	a and b
0	0	0
0	1	0
1	0	0
1	1	1

You should be able to figure out the table for the NOT gate, which we'll also refer to as an inverter gate, or simply inverter.

Integrated Circuit, AND gate. D. Thiebaut, 2014, Released under the Creative Commons Attribution 2.0 Generic license.

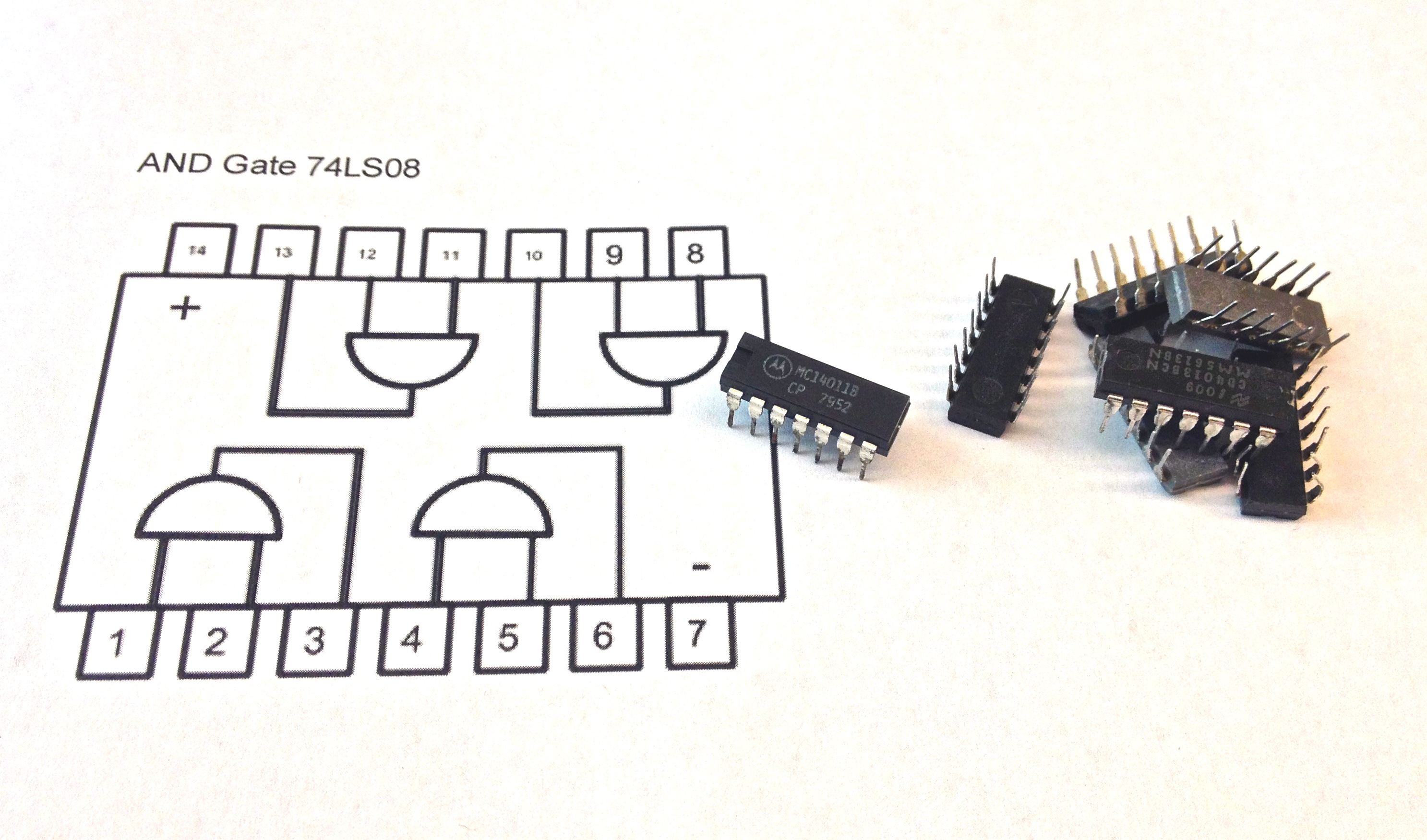
The image on the left, above, shows an integrated circuit (IC)close up. In reality the circuit is about as long as a quarter (and with newer technology even smaller). The image on the right shows what is inside the IC. Just 4 AND gates. There are other ICs that contain different types of gates, such as OR gates or Inverters.

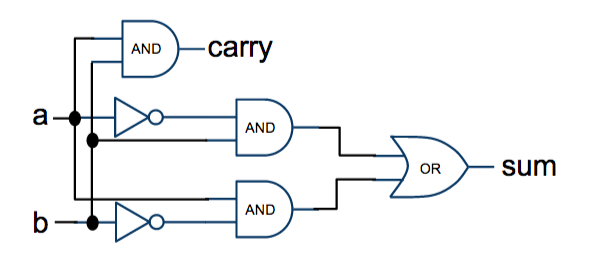
Building a Two-Bit Adder with Logic Gates

Designing the schematics for an electronic circuit from boolean function is very easy once we do a few examples:

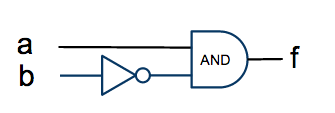
For example, imagine that we have a boolean function f of two variables a and b equal to:

f = a AND ( NOT b )

To implement it with logic gates we make a and b inputs, and f the output of the circuit. Then b is fed into an inverter gate (NOT), and the output of the inverter into the input of an AND gate. The other input of the AND gate is connected to the a signal, and the output becomes f.

A and Not B, D. Thiebaut, 2014, Released under the Creative Commons Attribution 2.0 Generic license.

Given the equations for the sum and carry signals that we generated earlier, we can now compose them using logic gates as shown below:

2-Bit Adder, D. Thiebaut, 2014, Released under the Creative Commons Attribution 2.0 Generic license.

---

---

---

---

...

References

.