Difference between revisions of "CSC270 Homework 4 2011"
(→Submission) |
|||
| Line 8: | Line 8: | ||
__TOC__ | __TOC__ | ||
<br /> | <br /> | ||
| − | <center> | + | <!--center> |
<font size="+2">Page under construction!</font> | <font size="+2">Page under construction!</font> | ||
<br \>[[File:UnderConstruction.jpg|300px]] | <br \>[[File:UnderConstruction.jpg|300px]] | ||
| − | </center> | + | </center--> |
<br /> | <br /> | ||
=Problem #1= | =Problem #1= | ||
Revision as of 10:58, 19 February 2011
--D. Thiebaut 10:42, 19 February 2011 (EST)
This assignment is about multiplexers and RS flipflops. You can work on this assignment in pairs if you wish. The due date is next Friday, at midnight.
Contents
Problem #1
- Implement a majority voter with a 4-to-1 multiplexer.
- Show the Karnaugh map and logic diagram that you use to find your answer.
- Similarly, use an 8-to-1 multipler and implement the same majority voter.
Problem #2
- We saw earlier that we can easily verify a design/circuit by generating its truth table with a Python program.
- How would we represent a 3-to-8 decoder circuit in Python?
- How about a 4-to-1 multiplexer (mux)?
- Prove that your two solutions for Problem 1 are correct by coding them in Python. Include the code and the output of the Python answer in your homework.
Problem #3
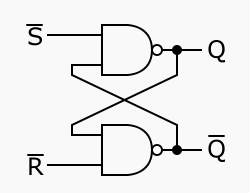
- The SR flipflop is the basic element of sequencial circuit. Its main property is memory. It can be used to remember a bit, either 0, or 1. Storing a bit in the flipflop is performed by activating one of the two inputs.
- If we were to switch one of the NANDs in the circuit above for a NOR, would we still have a flipflop? Why or why not?
- If we were to replace both NANDs by two exclusive-ORs, would we still have a flipflop, i.e. a circuit that has memory, in which we can store either 1 or 0?
Submission
- Write your answers in a pdf called hw4.pdf and submit it to your 270b-xx account as usual.