Difference between revisions of "CSC111 Lab 12 2015"
(→Program Name) |
(→Thinking Recursively) |
||
| Line 119: | Line 119: | ||
All the challenges below require you to put together a recursive function for a simple problem. | All the challenges below require you to put together a recursive function for a simple problem. | ||
| − | Thinking recursively is | + | Thinking recursively is quite challenging and takes a while to master. So don't despair! |
| − | Here | + | Here are points to remember when building a recursive function: |
<br /> | <br /> | ||
<tanbox> | <tanbox> | ||
| − | :# First figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's should expect to receive back from a call to itself.<br /><br /> | + | :# First, figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's what it should expect to receive back from a call to itself.<br /><br /> |
:# What is the '''stopping condition'''? What is the smallest problem you can solve without recursion? That's the first thing you want to test for and do in your recursive function.<br /><br /> | :# What is the '''stopping condition'''? What is the smallest problem you can solve without recursion? That's the first thing you want to test for and do in your recursive function.<br /><br /> | ||
:# If the stopping condition doesn't apply, and the function has to do some work, figure out how to make one or several recursive calls to the function, get some intermediate results back, combine them together and get the final answer. That's the '''recursive step'''.<br /> | :# If the stopping condition doesn't apply, and the function has to do some work, figure out how to make one or several recursive calls to the function, get some intermediate results back, combine them together and get the final answer. That's the '''recursive step'''.<br /> | ||
| Line 151: | Line 151: | ||
[[Image:QuestionMark2.jpg|right|120px]] | [[Image:QuestionMark2.jpg|right|120px]] | ||
<br /> | <br /> | ||
| − | * Given a number ''n'', compute recursively the sum of all the even | + | * Given a number ''n'', compute recursively the sum of all the positive '''even''' numbers less than or equal to n. |
* This is trickier than it seems! Here is an example of running a loop and asking the recursive function to compute the sum of all the even numbers up to ''n'' when ''n'' ranges from 0 to 12. | * This is trickier than it seems! Here is an example of running a loop and asking the recursive function to compute the sum of all the even numbers up to ''n'' when ''n'' ranges from 0 to 12. | ||
<br /> | <br /> | ||
| Line 176: | Line 176: | ||
[[Image:QuestionMark3.jpg|right|120px]] | [[Image:QuestionMark3.jpg|right|120px]] | ||
<br /> | <br /> | ||
| − | * Write a recursive function that returns the largest element of a list L using the following formula: | + | * Write a '''recursive function''' that returns the largest element of a list L using the following formula: |
<br /> | <br /> | ||
<br /> | <br /> | ||
| Line 196: | Line 196: | ||
|} | |} | ||
| − | :Test your program on different | + | :Test your program on different lists of varying sizes. We assume that the lists will always have at least one element. |
: ''' ''Hints'' ''' | : ''' ''Hints'' ''' | ||
Revision as of 13:58, 19 April 2015
--D. Thiebaut (talk) 11:31, 19 April 2015 (EDT)
Contents
|
This lab deals with recursive functions. Programming recursive functions is a challenging concept to master. The best way to proceed is to write many different recursive solutions and observe the behavior of the functions as they perform their work. Eventually recursion will start making sense. It is normal to not fully understand it at first. Keep at it. Little by little, it will become natural thinking. |
Visualizing Recursive Factorial At Work
Create a copy of this simple example:
# factorial.py # Demonstrates a recursive factorial function def fact( n ): # stopping condition if n<=1: return 1 # recursive step y = fact( n-1 ) result = n * y return result def main(): n = int( input( "Enter a positive number: " ) ) x = fact( n ) print( "the factorial of %d is %d." % ( n , x ) ) main()
- Run your program
- It will prompt you for a number and will return its factorial.
- Verify that it computes the correct result. Below are some factorials numbers to compare your output to.
1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 6! = 720 7! = 5040 8! = 40320 9! = 362880 10! = 3628800 11! = 39916800 12! = 479001600 13! = 6227020800 14! = 87178291200
Visualizing, Step 1
- Add print statements to your fact() function so that it will let you know exactly what it does. For example, before it tests to see if n is less than equal to 1, you could print:
print( "fact function started. Receives n =", n )
print( "testing if %d is >= 1" % (n) )
- Add print statements that will show the values of y and result.
- Run your program and observe its output. Can you see better how the function fact() recursively calls itself?
Visualizing, Step 2
- Create the more sophisticated program shown below. Observe it well first, and try to figure out what the indent variable does.
# factorialPrint.py # Demonstrates a recursive factorial function def fact2( n, indent ): print( indent, "fact2(%d) started" % n ) print( indent, "comparing %d to 1" % n ) if n<=1: print( indent, "%d is <= 1. Returning 1" % 1 ) return 1 print( indent, "%d is not <= 1. Calling fact2(%d) and storing it in y" % (n, n-1) ) y = fact2( n-1, indent + " " ) print( indent, "just received %d from fact2( %d )." % ( y, n-1 ) ) result = n * y print( indent, "multiplied %d by %d. It's %d. Returning %d to caller" % ( n, y, result, result ) ) return result def main(): n = input( "Enter a positive integer: " ) print( "Main calls fact( %d )" % n ) y = fact2( n, " " ) print( "Main receives result = ", y ) main()
- Run the program
- Explain the pattern made by the printed lines. Why this shape?
- Where does the stopping condition appear in the printed lines? In other words, where is the printed statement that indicates that fact() just received a value of n equal to 1? Why isn't this statement at the end of the printout?
Thinking Recursively
All the challenges below require you to put together a recursive function for a simple problem.
Thinking recursively is quite challenging and takes a while to master. So don't despair!
Here are points to remember when building a recursive function:
- First, figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's what it should expect to receive back from a call to itself.
- What is the stopping condition? What is the smallest problem you can solve without recursion? That's the first thing you want to test for and do in your recursive function.
- If the stopping condition doesn't apply, and the function has to do some work, figure out how to make one or several recursive calls to the function, get some intermediate results back, combine them together and get the final answer. That's the recursive step.
- First, figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's what it should expect to receive back from a call to itself.
Challenge 1: Recursive Sum |
- Given a number n, compute recursively the sum of all the numbers from 1 to n. For example, if you pass n = 5 to the solution function, it will return 15 (which is equal to 5+4+3+2+1)
Challenge 2: Recursive Even Sum |
- Given a number n, compute recursively the sum of all the positive even numbers less than or equal to n.
- This is trickier than it seems! Here is an example of running a loop and asking the recursive function to compute the sum of all the even numbers up to n when n ranges from 0 to 12.
n = 0 sumEven(0) returns 0 n = 1 sumEven(1) returns 0 n = 2 sumEven(2) returns 2 n = 3 sumEven(3) returns 2 n = 4 sumEven(4) returns 6 n = 5 sumEven(5) returns 6 n = 6 sumEven(6) returns 12 n = 7 sumEven(7) returns 12 n = 8 sumEven(8) returns 20 n = 9 sumEven(9) returns 20 n = 10 sumEven(10) returns 30 n = 11 sumEven(11) returns 30
Challenge 3: Recursive Max |
- Write a recursive function that returns the largest element of a list L using the following formula:
|
largest( L ) |
= L[0] |
if len( L ) == 1 |
|
|
= max( L[0], largest( L[1:] ) ) |
otherwise. We assume N=len(L) |
- Test your program on different lists of varying sizes. We assume that the lists will always have at least one element.
- Hints
- the function definition is simply def largest( L ):
- write the stopping condition first (if len(L)...)
- if the stopping condition is not met, compute the max() of L[0] and largest( L minus the first element )
def largest( A ):
if len( A )==1:
return A[0]
return max( A[0], largest( A[1:] ) )
Divide and Conquer Recursion
- We now take a slightly different approach. This time we take a list, divide it two halves, recursively process the two halves, and combine the result of the results obtained on both sides.
- As an example, assume we have to find the largest item in a list L. Here's a possible way to describe the recursive divide-and-conquer approach:
|
largest( L ) |
= L[0] |
if len( L ) == 1 |
|
|
= max( largest( L[0:N/2], largest( L[N/2:] ) ) |
otherwise. We assume N=len(L) |
The code equivalent to this definition is shown below:
def divideConquerLargest( L ): N = len( L ) if N==1: return L[0] return max( divideConquerLargest( L[0:N//2] ), divideConquerLargest( L[N//2: ] ) )
- Run this code, and verify that it returns the largest element of an unsorted list of integers.
L = [1, 2, 3, 0, 10, 20, 30, 3, -3, 5, 1, 100, 1] print( "divideConquerLargest( %s ) = %d" % (L, divideConquerLargest(L ) ) )
Challenge 4: Divide-and-Conquer Min |
- Write a recursive function that uses the divide and conquer approach to find the smallest element in a list L.
Challenge 5: Divide-and-Conquer Sum |
- Write a recursive function that uses the divide and conquer approach to compute the sum of all the elements in a list L.
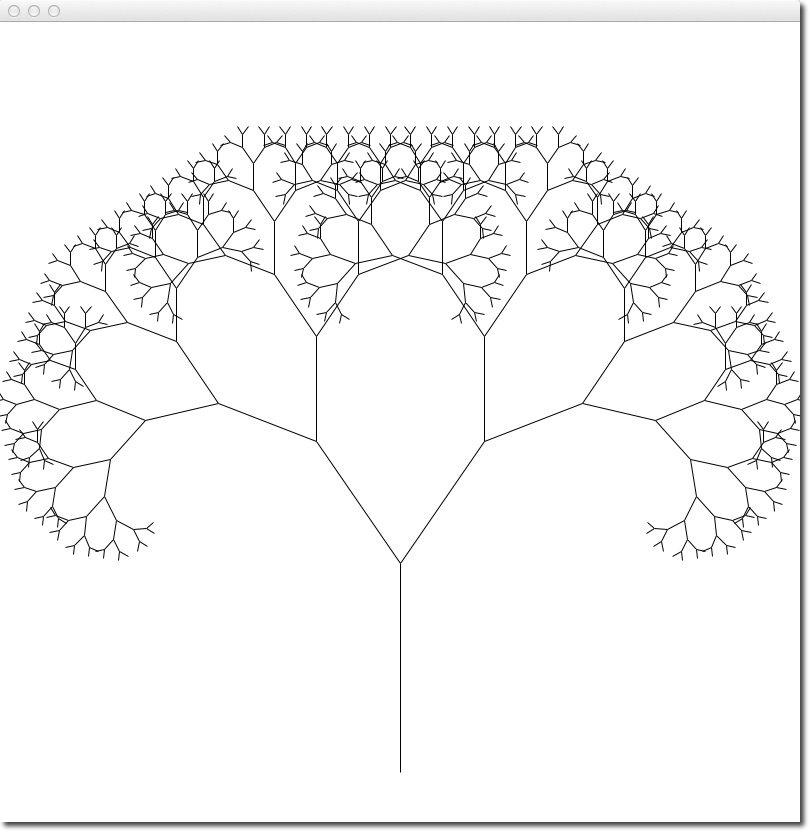
Fractal Trees
This is just something for you to play with. You do not have to include this into your lab13.py program. Just create a new program with the code you'll find on this page, put it in the same directory where you store your graphics111.py directory. You may want to call your program fractalTree.py.
The program generates a fractal tree. Fractals are self-similar objects: they look the same on a small scale as they do on a larger scale.
- Run the program first
- Then look at the code and see if you can figure out how the recursion works.
- To see how the different parameters influence the drawing of the fractal tree, modify the following parameters, one at a time, and give them different values:
- theta
- in the main program, change the angle theta which controls how much a branch will diverge from the direction of the branch that supports it. Try 0.4 first. Then try values between 0 and 0.8.
- level of recursion
- the main program passes 9 to the function as a starting level of recursion. Try passing smaller numbers first, then larger numbers (but less than 13 or so).
- trunk_ratio
- recursive function defines this as 0.29 and that represents the length of the trunk relative to its two branches. Try ratios between 0.1 (10%) and 0.9 (90%).
Submission
Submit the program lab13.py to this URL: http://cs.smith.edu/~thiebaut/111b/submitL13.php.
Exercise 1: Factorial
Create a copy of this simple example:
# lab12_1.py
# A simple program that uses a recursive function to compute
# the factorial of a number.
def fact( n ):
if n<=1:
return 1
y = fact( n-1 )
result = n * y
return result
def main():
n = int( input( "Enter a positive number: " ) )
x = fact( n )
print( "the factorial of", n, "is", x )
main()
- Run your program
- It will prompt you for a number and will return its factorial.
- Verify that it computes the correct result. Below are some factorials numbers to compare your output to.
1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 6! = 720 7! = 5040 8! = 40320 9! = 362880 10! = 3628800 11! = 39916800 12! = 479001600 13! = 6227020800 14! = 87178291200
- Question 1
-
- Add print statements to your fact() function so that it will print exactly what it does. For example, before it tests to see if n is less than equal to 1, you could print:
print("fact function started. Receives n =", n )
print( "testing if", n, "is >= 1" )
- Add print statements that will show the values of y and result.
- Run your program and observe its output. You should be able to better observe how the function fact() recursively calls itself?
Exercise 2: A Factorial with Annotation
- Create the more sophisticated program shown below. Observe it well first, and try to figure out what the indent variable does.
# factorialPrint.py # Demonstrates a recursive factorial function and the nesting created by the function calling itself. # def fact( n, indent ): print( indent, "fact(", n, ") started" ) print( indent, "comparing", n, "to 1" ) if n<=1: print( indent, n, "is <= 1. Returning 1" ) return 1 print( indent, n, "is not <= 1. Calling fact(", n-1, ") and storing it in y" ) y = fact( n-1, indent + " " ) print( indent, "just received", y, " when fact(", n-1, ") returned." ) result = n * y print( indent, "multiplied", n, "by", y," Returning", result," to caller" ) return result def main(): # print first 15 factorials n = int( input( "Enter a positive integer: " ) ) print( "Main calls fact(", n,")" ) y = fact( n, " " ) print( "Main receives result in y = ", y ) main()
- Run the program
- Explain the pattern made by the printed lines. Why this shape?
- Where does the stopping condition appear in the printed lines? In other words, where is the printed statement that indicates that fact() just received a value of n equal to 1? Why isn't this statement at the end of the printout?
Exercise: Finding the largest in a series of numbers
- For this exercise, we must forget that the max() function can return the largest of a list of numbers in one swoop. Instead, we want to write a recursive function that finds the largest of a list of numbers.
- Write a program that includes a recursive function called largest( ). The function receives a list of numbers as parameter, and returns the largest element of a list using the following recursive formula:
largest( A ) = A[0] if len( A ) == 1 = max( A[0], largest( A[1:] ) ) otherwise
- Test your program on different lists of varying length. We assume that the list of numbers will always have at least one element.
- Hints
- the function definition is simply def largest( A ):
- write the stopping condition first (if len(A)...)
- if the stopping condition is not met, compute the max() of A[0] and largest( A minus the first element )
def largest( A ):
if len( A )==1:
return A[0]
return max( A[0], largest( A[1:] ) )
Exercise: Finding the smallest element
Write a similar function that finds the smallest element of a list of numbers, recursively. You can use the min() function, but only to find the smallest of 2 numbers.
Exercise: Finding the longest word in a text
Write a recursive function that is given a list of words and returns the longest word in the list.
Exercise: Finding the shortest word in a text
Write a recursive function that is given a list of words and returns the shortest word in the list.
Binary Search
- Create a copy of the binary search program.
- Observe the main function. Make sure you figure out how large the array is.
- Run the program and verify that the search function does a good job reporting if a number is in the array of not.
- First problem
-
- Modify the program so that it counts the number of comparisons that it performs. A good way to do this is to create a global variable, we'll call it count, that is declared at the beginning of your program, and which you increment by one, every time the binsearch function compares two quantities. These comparisons are a good indicator of the amount of "work" done by the function, since it is obvious just looking at the program to figure out how much time the function will call itself.
- The correct way to use count as a global variables is illustrated below. You initialize the variable at the beginning of the program, and in the functions that need to use it, you define count as global so that python will know that count is not just a local variable used inside the function, but refers to something defined outside the function.
# program header # count = 0 def binsearch( ... ): global count ... count += 1 def main(): global count ... count = 0 binarySearch( ... ) print( count )
- Make the main program print the number of comparisons performed after the function returns to main.
- Make sure you reset the counter to 0 for every new search!
- Second question
-
- Run your program several times for lists of size 20, 100, 1,000, 10,000, and 100,000.
- For each list size, record the number of comparisons it takes to find items
- What is the relationship between the size of the list and the (average) number of comparisons?
Exploring Fractal Trees
This is just something for you to play with. You do not have to include this into your lab13.py program. Just create a new program with the code you'll find on this page, put it in the same directory where you store your graphics111.py directory. You may want to call your program fractalTree.py.
The program generates a fractal tree. Fractals are self-similar objects: they look the same on a small scale as they do on a larger scale.
- Run the program first
- Then look at the code and see if you can figure out how the recursion works.
- To see how the different parameters influence the drawing of the fractal tree, modify the following parameters, one at a time, and give them different values:
- theta
- in the main program, change the angle theta which controls how much a branch will diverge from the direction of the branch that supports it. Try 0.4 first. Then try values between 0 and 0.8.
- level of recursion
- the main program passes 9 to the function as a starting level of recursion. Try passing smaller numbers first, then larger numbers (but less than 13 or so).
- trunk_ratio
- recursive function defines this as 0.29 and that represents the length of the trunk relative to its two branches. Try ratios between 0.1 (10%) and 0.9 (90%).
Exercise: Exploring a Maze
Here is an example of a complex problem that can be (relatively) easily solved using a recursive program.
- Get a copy of the maze-visiting program, and run it.
getcopy visitMaze.py
- Observe how the recursive visitMaze() function leaves "bread crumbs" behind the cells that it visits, and "v" characters in cells visited but known not to lead to an exit.
- Edit the program and switch the order in which the function visits cells in the 4 directions. Make the recursive function decide to go up first, then left, then right, and finally down.
- Run the program and see how this change influences the way the program explores the maze.
- Modify your program so that the maze is now a much simpler maze, in the spirit of the maze shown below:
mazeText = """
#########################
........................#
#.......................#
#.......................#
#...........#...........#
#...........#...........#
#############...........#
#...........#...........#
#.......................#
#........################
#........................
#.......................#
#.......................#
#########################
"""
- Predict the path that the program is going to take when visiting it.
- Repeat the same experiment as before and change the order in which the recursive function visits the different directions, and observe if this makes the function find the exit faster.
Treasures in the maze
- Let's change the rules of the game, and make your program find a path to a treasure, rather than a path to an exit. In our case the treasure will be a special character, say '&', inside the maze.
- Modify your the visitMaze() function so that it now returns true if it finds the treasure, and not an exit. Verify that your program displays at the end the path to the treasure.