Difference between revisions of "CSC270 Homework 2 2016"
(→Problem 1) |
(→Problem 1) |
||
| Line 12: | Line 12: | ||
* Is one, or both of the gates above universal? Why or why not? | * Is one, or both of the gates above universal? Why or why not? | ||
<br /> | <br /> | ||
| + | =Problem 2= | ||
| + | <br /> | ||
| + | * Simplify the following functions using Karnaugh maps. Please show the Karnaugh map and its covers in your answer. If you can simplify the functions further by using some of the theorems of Table 2.2, then do so. Basically write the function so as to minimize the number of operators ( dot, plus, prime). | ||
| + | |||
| + | f(a, b, c, d) = Σ (0, 1, 2, 3, 12, 13, 14, 15 ) | ||
| + | |||
| + | g(a, b, c, d) = Σ (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15 ) <font color = "magenta">// 11 missing!</font> | ||
| + | |||
| + | h(a, b, c) = Π ( 0, 1, 2, 3 ) | ||
| + | |||
| + | k(a, b, c) = Π (0, 1, 7, 8 ) | ||
| + | |||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | [[Category:CSC270]][[Category:Homework]] | ||
Revision as of 13:50, 4 February 2016
--D. Thiebaut (talk) 13:28, 4 February 2016 (EST)
This homework is due on 2/11/16 at 11:55 p.m. You can work individually or in a group of two.
Problem 1
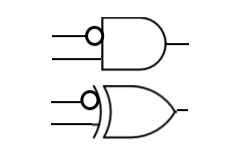
- The top gate, above, is an AND gate with an inverted input. The gate below it is an exclusive OR with an inverted input. The equation for the first one, assuming that the inputs are a and b, is a . (b'). The equation for the bottom one is a ⊕ b'
- Is one, or both of the gates above universal? Why or why not?
Problem 2
- Simplify the following functions using Karnaugh maps. Please show the Karnaugh map and its covers in your answer. If you can simplify the functions further by using some of the theorems of Table 2.2, then do so. Basically write the function so as to minimize the number of operators ( dot, plus, prime).
f(a, b, c, d) = Σ (0, 1, 2, 3, 12, 13, 14, 15 ) g(a, b, c, d) = Σ (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15 ) // 11 missing! h(a, b, c) = Π ( 0, 1, 2, 3 ) k(a, b, c) = Π (0, 1, 7, 8 )