Programming Contest 2011

From dftwiki3
Revision as of 13:50, 24 March 2011 by Thiebaut (talk | contribs)
Jump to: navigation, search
ProgrammingContestAndTeam2011.png




The TEAM

  • Julia Burch, '11
  • Janet Guo, '12
  • Yang Li, '11
  • (chauffeur: Dominique Thiebaut)




Contest Web Page




Date

  • April 15th 9am - Noon. The contest is held concurrently with the conference workshops and before the paper sessions.
    • Detailed Timeline
      • 7:45 - 8:45 a.m. Breakfast and Registration of Teams and Team Members Registration Area
      • 7:45 - 8:45 a.m. Computers available for practice TBA
      • 8:45 - 9:00 a.m. Initial Meeting and Presentation of the Problems TBA
      • 9:00 a.m. - Noon Contest TBA
      • Noon - 12:45 p.m. Luncheon for Programming Teams TBA
      • 7:00 - 9:00 p.m. Dinner / Announcement of Contest Winners TBA




Details

  • The programming languages for the contest are Java and C/C++.
  • Rules for the contest are similar to the ACM Programming Contest.
  • The winners of the contest will be announced at the Conference Banquet.
  • A trial website will be made available a month before the contest so teams can familiarize themselves with the contest shell.




Rules

These are the ACM Programming Contest Rules. The rules from the CCSCNE contest differ in a few ways, notably the length of time: 3 hours instead of 5. The text below is taken from http://en.wikipedia.org/wiki/ACM_International_Collegiate_Programming_Contest

The ICPC is a team competition. Current rules stipulate that each team consist of three students. Participants must be university students, who have had less than five years of university education before the contest. Students who have previously competed in two World Finals or five regional competitions are ineligible to compete again.[1][2]

During contest, the teams are given 5 hours (3 for the CCSCNE contest) to solve between 8 and 12 programming problems (with 8 typical for regionals and 10 for finals). They must submit solutions as programs in C, C++, or Java. Programs are then run on test data. If a program fails to give a correct answer, the team is notified about that and they can submit another program.

The winner is the team which correctly solves most problems. If necessary to rank teams for medals or prizes among tying teams, the placement of teams is determined by the sum of the elapsed times at each point that they submitted correct solutions plus 20 minutes for each rejected submission of a problem ultimately solved.

For example, consider a situation when two teams, Red and Blue, tie by solving two problems each. The team Red submitted their solutions to A and B at 1:00 and 2:45 after the beginning of the contest. They had a rejected run on C, but it was ignored since they didn't solve C. The team Blue submitted solutions to problems A and C at 1:20 and 2:00 after the beginning. They had one rejected run on C. Then, the total time is 1:00+2:45=3:45 for team Red and 1:20+2:00+0:20=3:40 for team Blue. The tie is broken in favor of Team Blue.

Compared to other programming contests (for example, International Olympiad in Informatics), the ICPC is characterized by a large number of problems (8 or more problems in just 5 hours). Another feature is that each team can use only one computer, although teams have three students. This makes the time pressure even greater. Good teamwork and ability to withstand pressure is needed to win.




Resources

I/O In Java

Basic Strategies




Sample Problems

Below are a few problems taken from The Competitive Learning Institute (CLI), where you can find more problems.

4900 - Cut It Out!

Television's Toddler Time's topic taught to toddler Tommy Tiwilliger today was triangles (and the letter T)! Tommy became so enamored by triangles that immediately after the show ended, he grabbed his safety scissors and the nearest sheets of paper he could find and started cutting out his own triangles. After about 15 minutes each paper had one triangular shaped hole cut out of it. But Tommy wasn't finished yet. He noticed he could divide each of the original triangles into two triangles with a single cut starting from one corner. He spent another 15 minutes doing just that. Things would have gone along swimmingly, except that Tommy's mother eventually came into the room and noticed that the original sheets of paper were part of a very important document for a legal case she was working on (involving a lover's triangle). After carefully removing Tommy from the room and counting slowly to 10 (a triangular number), she went about trying to reconstruct the pages after gathering together the now randomly scattered triangles. Your job is to help her by writing a little program to determine which triangles go where (and try to get it done before tomorrow's episode of Toddler Time on papier- mâchè).

Input

Each test case will start with an integer n 20 indicating the number of holes cut out, followed by the coordinates of the holes, one hole per line. These holes are assumed to be numbered 1, 2,..., n. Following this will be the coordinates of the 2n triangles resulting from the bisections, one triangle per line. These triangles are assumed to be numbered 1, 2,..., 2n and are listed in no particular order. The specification of any hole or triangle will have the form x 

1
y
1
x
2
y
2
x
3
y
3

where each xi and yi will be to the nearest thousandth and | xi|,|yi| 200.

No two holes will be congruent and no two triangles will be congruent. A value of n = 0 will terminate input.

Output

For each test case, you should output the case number and then n lines as follows: 

Hole 1: t1a, t1b 
Hole 2: t2a, t2b
...
Hole n: tna, tnb

where t1a, t1b are the two triangles which fill hole 1, t2a, t2b are the two triangles which fill hole 2, etc. Always print the lower of the two numbers first on any line. Triangles should not be flipped over when filling a hole. Each test case will have a unique solution. Separate the output for each test case with a blank line. Note: when processing the triangles and checking for equality of lengths, angles or trigonometric values, you may assume that two items are equal if they differ by less than 0.01.

Sample Input

1 
18.691 6.103 21.668 13.709 21.332 25.894 
59.388 30.873 55.299 36.186 61.45 22.97 
4900 - Cut It Out! 1/267.828 85.496 60.751 72.752 59.2 67.49 
3 
18.73 4.012 6.662 7.557 14.035 7.478 
14.869 32.398 32.341 31.772 7.522 29.674 
25.272 6.868 4.572 2.014 10.487 16.121 
26.135 53.073 44.18 50.723 40.31 42.91 
86.601 29.95 70.542 17.088 66.77 14.88 
90.344 89.528 92.179 88.665 87.99 82.54 
39.327 62.11 35.033 57.127 18.14 63.89 
37.13 80.202 36.308 75.111 34.28 75.11 
14.043 68.482 15.22 55.423 10.42 75.43 
0

Sample Output

Case 1:  
Hole 1: 1, 2 
Case 2:  
Hole 1: 3, 5
Hole 2: 2, 6
Hole 3: 1, 4

Flip It!

Assume you have a set of cards laid out in an n by m grid. The cards are numbered and some are face up and others are face down. We can collapse the grid into a single pile by using a series of flips, each of which is one of the four following types:

Top Flip :

Here the cards in the top row are flipped over onto the corresponding cards on the row beneath them. Note that if a card is face up in the top row, it becomes face down after the flip, and vice versa. If the top row contains one or more piles of cards, each entire pile is flipped over like a stack of pancakes as it is moved to the lower row.

Bottom Flip :

Same as the Top Flip, but now the bottom row is flipped onto the next-to-bottom row.

Left Flip :

Flip the cards in the left-most column onto the next-to-leftmost column.

Right Flip :

Flip the cards in the rightmost column onto the next-to-rightmost column. After a series of n + m - 2 flips, the cards will be in a single pile, some cards face up and some face down. Your job is to determine the order of the face up cards in this final pile.

Input

Each test case will start with a line containing two positive integers n m indicating the number of rows and columns in the grid. After this will come n rows of m integers indicating each card's number and its orientation. (The first row is the top row and the first value in each row is the leftmost card.) If a value is a positive integer k that means card k is at the location face up; if a value is a negative integer - k that means card k is at the location face down. (k will never be zero.) After these n rows there will be one more line containing n + m - 2 characters indicating the order of flips to apply to the grid. Each character will be either T, B, L or R corresponding to a top, bottom, left or right flip. All flip sequences will be legal, i.e., you won't be asked to do more than n - 1 top and bottom flips or m - 1 left and right flips. The maximum value for n and m is 20. A line containing two zeros will terminate input.

Output

For each test case, output the case number followed by a list of the numbers of all of the face up cards in the final deck, starting from the bottom of the deck. Follow the format used in the examples.

Sample Input

2 3 
4 -17 -8 
6 23 -5 
LRB 
1 1 
-3 

1 1 
3 

0 0

====Sample Output ====

Case 1: 8 6 
Case 2: 
Case 3: 3


Maze

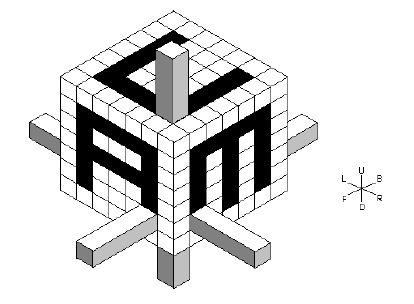
ProgrammingContestMaze.png

We are all familiar with conventional mazes laid out on a 2-D grid. A 3-D maze can be constructed as follows: Consider a hollowed out cube aligned along the x, y and z axes with one corner at (0,0,0) and the opposite corner at (n - 1, n - 1, n - 1). On each face of the cube is a 2-D maze made by removing a subset of 1 x 1 x 1 cubes from the face (no edge cubes are removed). The object of the maze is to move a marker located inside the cube from an initial location of (1,1,1) to the final destination of (n - 2, n - 2, n - 2). However, attached to this marker are 6 rods, each protruding through one face of the cube. The movement of these rods is constrained by the 2-D mazes on the faces. The picture below gives an example of a 7 x 7 x 7 maze. Note that this maze is not physically realizable since some faces (e.g., the front face containing the letter ``A") have cubes that are disconnected from the edges of the face. Such mazes are allowed in this problem.


The black regions indicate open spaces where the rods can move. The figure to the right specifies the possible directions that the rods can move (Forward, Back, Left, Right, Up, Down) and also defines the labels for the six sides of the cube. In the maze above, the rods are shown in their initial position centered at (1,1,1). From here they can not move Forward, Backward, Right, Left or Down, but they can move Up (assuming there are open spaces for the two back rods to move to).

To specify a cube, a description of each face must be given. For this problem, the order and orientations of each face are given in the diagram below.


The first square represents the Forward face oriented so that the shared edge with the Up face is on top and the shared edge with the Right face is on the right, the second square represents the Right face oriented with the shared edge with the Up face on top and the shared edge with the Back face on the right, and so on. Your job is to solve such mazes in the minimum number of moves.

Input

Each test case will start with a single line containing the value of n, where n lies between 4 and 30, inclusive. Next will come descriptions of each face in the order and orientation shown above. The description of each face will consist of n lines each containing one string of length n. The characters in the string will be either a blank or `X', indicating either an empty or full square, respectively. The last test case will be followed by a line containing 0.

Output

Output will consist of one line for each test case. Each line will contain a description of a minimum-move solution that moves the marker from cell (1,1,1) to cell (n - 2, n - 2, n - 2). Moves are either F, B, L, R, U or D. In case of a tie, choose the sequence of moves which is lexicographically first, where we consider F < B < L < R < U < D. All mazes will have solutions. 

Sample Input 

7 
XXXXXXX 
X     X 
X XXX X 
X     X 
X XXX X 
X XXX X 
XXXXXXX 
XXXXXXX 
X     X 
X X X X 
X X X X 
X X X X 
X X X X 
XXXXXXX 
XXXXXXX 
X     X 
X     X 
X     X 
X     X
X     X 
XXXXXXX 
XXXXXXX 
X     X 
X X X X 
X     X 
X X X X 
X     X 
XXXXXXX 
XXXXXXX 
X XXX X 
X XXX X 
X XXX X 
X XXX X 
X     X 
XXXXXXX 
XXXXXXX 
X     X 
X XXX X 
X XXX X 
X XXX X 
X     X 
XXXXXXX 
0
Sample Output 

UULLLLUUBBBB
Retrieved from "http://dominiquethiebaut.com/dftwiki3/index.php?title=Programming_Contest_2011&oldid=11067"