CSC270 Homework 1 2011
--D. Thiebaut 16:13, 27 January 2011 (EST)
This assignment is due Friday 2/4/11 at 3:00 p.m. if submitted on paper, or at midnight if submitted electronically. No late assignment will be accepted. You can skip one assignment without penalty during the semester.
Contents
Problem #1
- Write the most concise expression (as an equation using + . and the bar over a symbol) of the boolean function f( a, b, c ) = Σ(0, 1, 2, 3, 7 ).
- Same question for g( a, b, c ) = Σ(0, 1, 2 )
- Same question for h( a, b, c ) = Σ(0, 1, 2, 3, 4, 5, 6, 7 )
- Same question for k( a, b, c ) = Σ(0, 1, 2, 3, 4, 6, 7 )
Problem #2
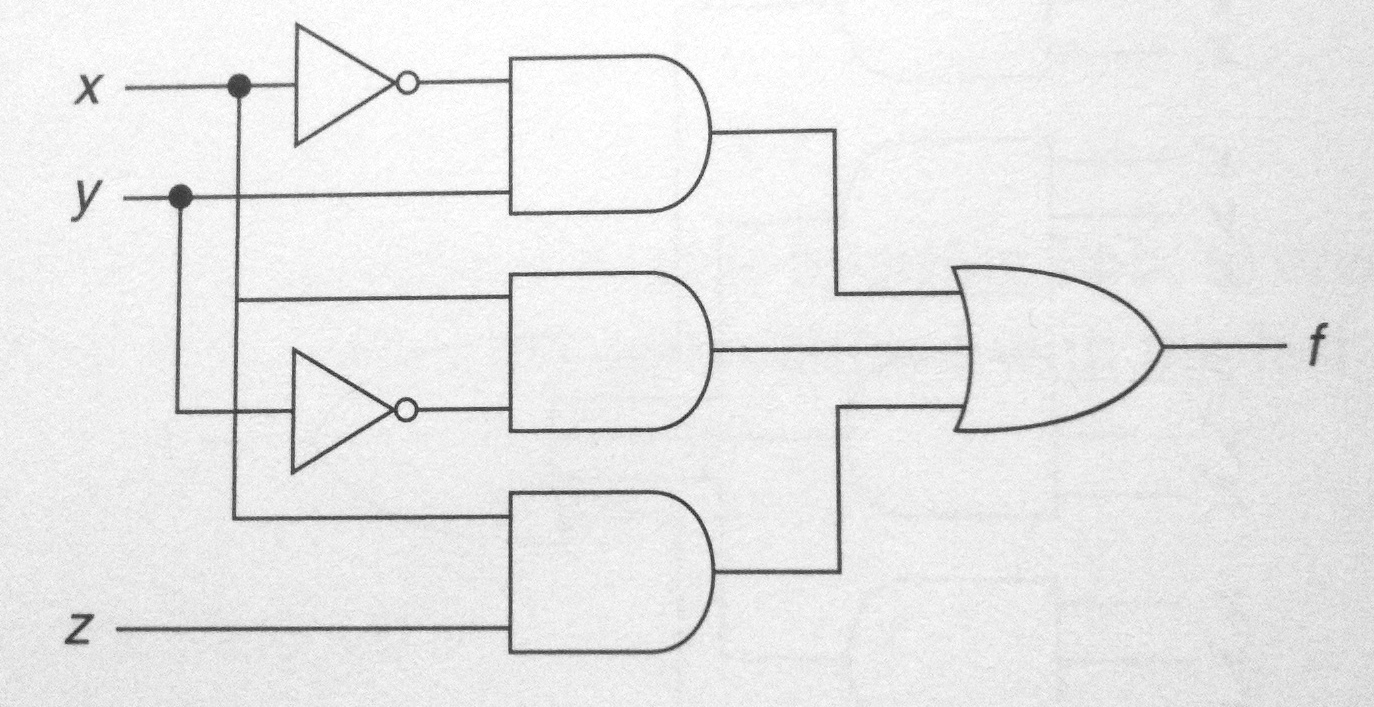
- What is the raw expression of the function f shown below? In other words, what is its direct translation of the diagram, without any simplification on your part? (Note the wire going from x to the second AND gate from the top should have a dot on it, to indicate that the signal is split from one wire to two.)
- What is the most concise expression of f?
- What are the minterm and Maxterm canonical forms of f? Develop the Maxterm form of f wihout using the Π() notation, but instead representing it as a product of sums.
Problem #3
- What are the Maxterm canonical forms of the functions of Problem #1?