CSC231 Exercises with Signed Numbers

--D. Thiebaut 09:37, 1 October 2012 (EDT)

---

Binary Addition in Various Systems

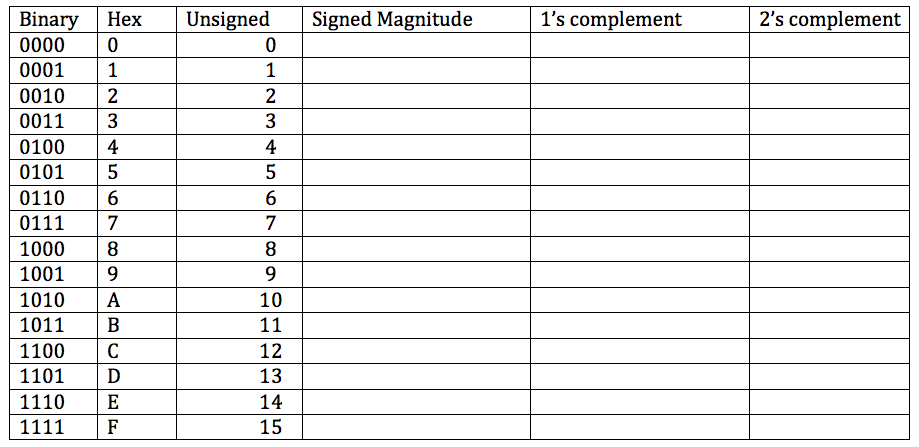
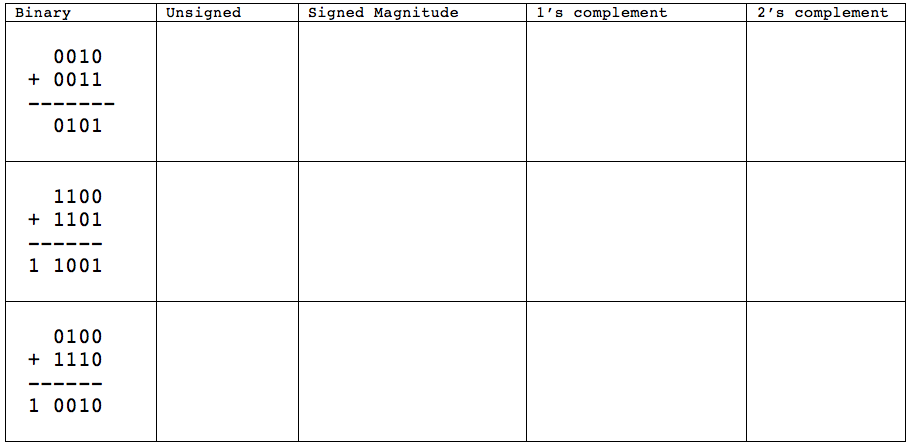
Exercise 1

What is the range of numbers in a 4-bit unsigned system? in a 4-bit 2's complement system? in an 8-bit unsigned system? In an 8-bit 2's complement system?

(Revisit the handout on Java's range of data types.)

Exercise 2

An program written in some unspecified language contains an array of 10 bytes. The values of the 10 bytes are 0x10, 0xff, 0xf1, 0x00, 0x00, 0xfe, 0x73, 0x01, 0x02, 0x7f.

Are these values used to represent signed numbers, unsigned numbers, numbers in 2's complement, numbers in 1's complement, or numbers in signed magnitude?

Exercise 3

• what is the 8-bit representation of the following decimal numbers in signed magnitude, 1's complement, and 2's complement?

0

 
1

 
-1 


11


-11


127


-127
   

128


-128

Exercise #4

• Convert the following signed, 2's complement 16-bit binary numbers to their decimal equivalent.

 0000 0000 0000 0001

 1000 0000 0000 0001

 0000 0000 1111 1111

 1111 1111 1111 1111

Exercise 5

• Perform the binary addition of the following decimal numbers using 2's complement, and assuming the numbers are 16-bit words

(for reference, 23 decimal = 10111 binary, 100 decimal = 1100100 binary)

 23 - 100 =

 23 - 23 =

100 - 23 =

Exercise 6

• A badly written software program is supposed to monitor and display the temperature recorded by a thermometer. This thermometer is used in chemical beaker. During an important experiment, the display outputs the following values:

56 59 70 81 99 110 -125

• What was the most likely true value of the last temperature recorded?
• (For reference, 125 in binary is 0111 1101, and -125 in 2's complement is 1000 0011.)

Solutions

...