CSC270 Homework 1 2011
--D. Thiebaut 16:13, 27 January 2011 (EST)
This assignment is due Friday 2/4/11 at 3:00 p.m. if submitted on paper, or at midnight if submitted electronically. No late assignment will be accepted. You can skip one assignment without penalty during the semester. This assignment must be done individually, and cannot be done in a group.
Problem #1
- Write the most concise expression (as an equation using + . and the bar over a symbol) of the boolean function f( a, b, c ) = Σ(0, 1, 2, 3, 7 ).
- Same question for g( a, b, c ) = Σ(0, 1, 2 )
- Same question for h( a, b, c ) = Σ(0, 1, 2, 3, 4, 5, 6, 7 )
- Same question for k( a, b, c ) = Σ(0, 1, 2, 3, 4, 6, 7 )
Problem #2
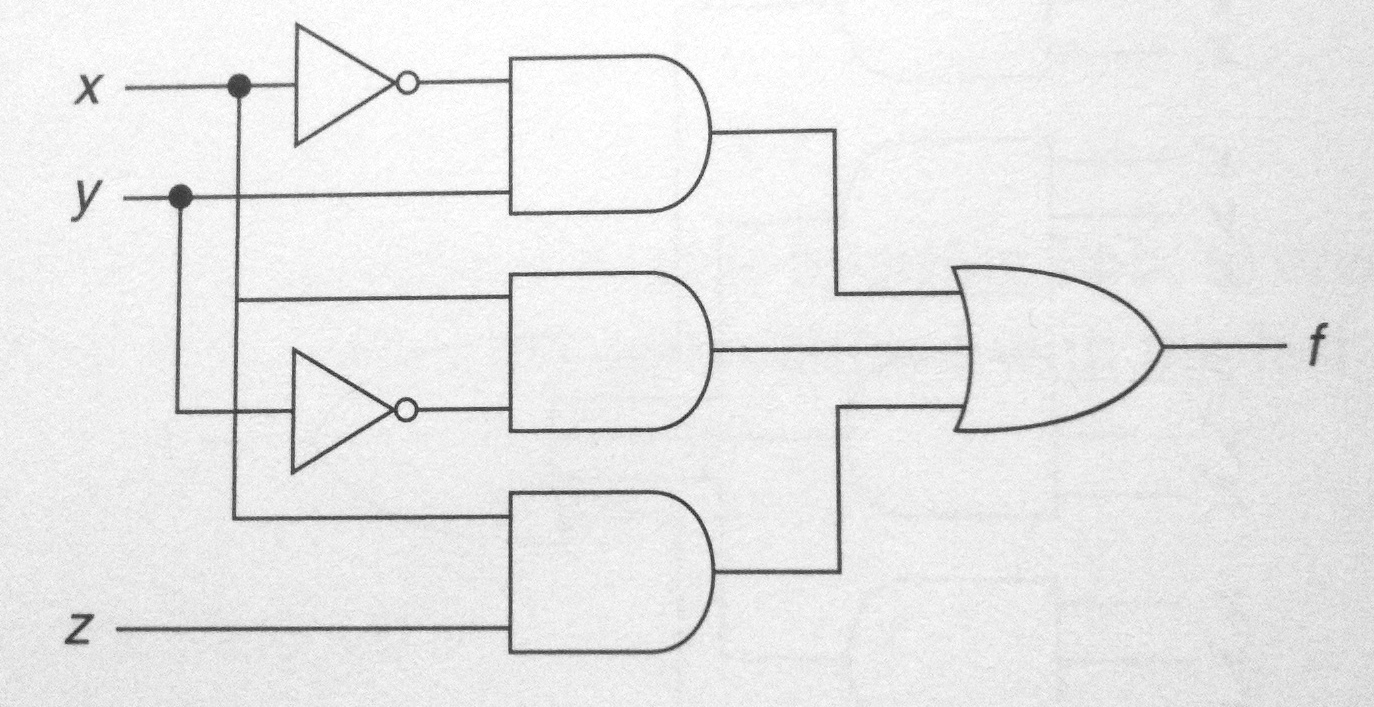
- What is the raw expression of the function f shown below? In other words, what is its direct translation of the diagram, without any simplification on your part? (Note the wire going from x to the second AND gate from the top should have a dot on it, to indicate that the signal is split from one wire to two.)
- What is the most concise expression of f?
- What are the minterm and Maxterm canonical forms of f? Develop the Maxterm form of f wihout using the Π() notation, but instead representing it as a product of sums.
Problem #3
- What are the Maxterm canonical forms of the functions of Problem #1? Show the result in two different format, one using Π() and the other showing the function as a product of sums.