CSC270 Exercises: Karnaugh Maps, Nands, Nors

From dftwiki3
Revision as of 10:26, 6 February 2011 by Thiebaut (talk | contribs) (→‎NANDs and NORs)
Jump to: navigation, search

--D. Thiebaut 10:16, 6 February 2011 (EST)

NANDs and NORs

  • The current homework asks you to implement the circuit below with NAND gates only. For this exercise, implement it with NOR gates only
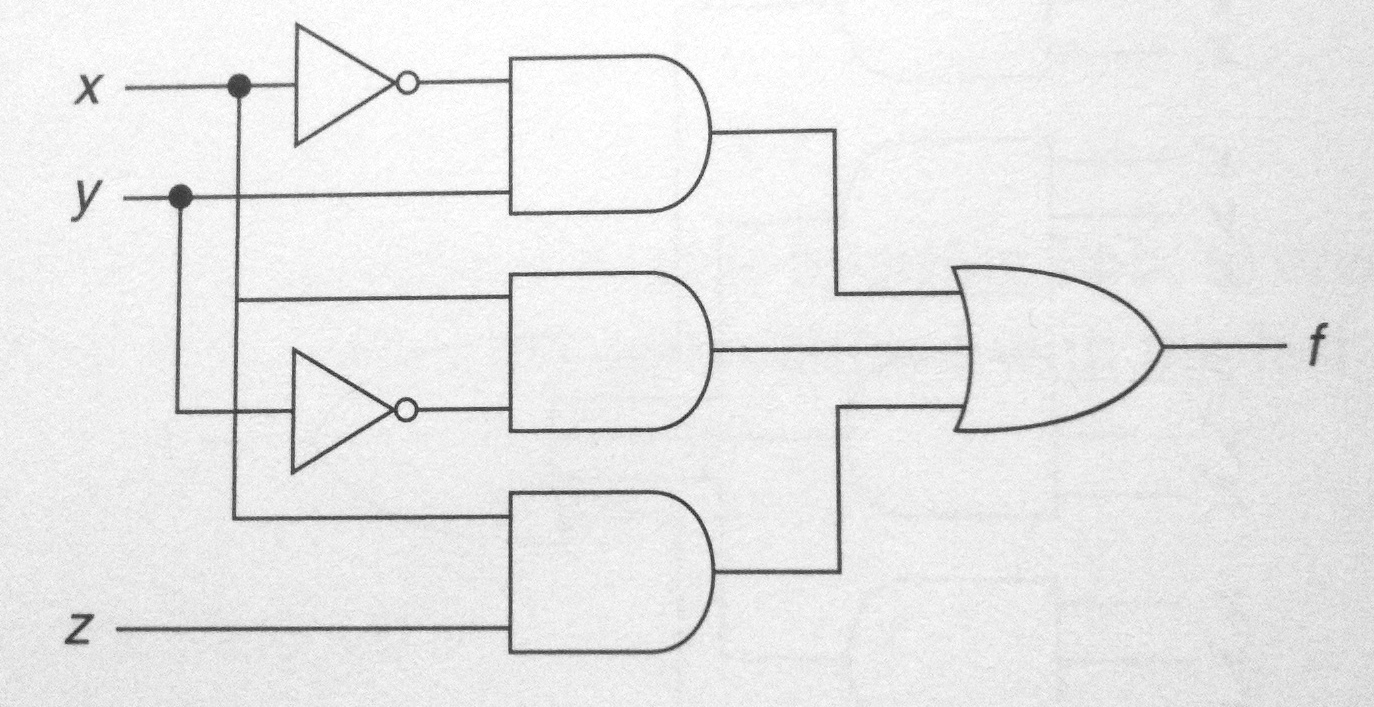
CSC270LogicCircuitHomework1.jpg
    • First approach: find the boolean expression for the output, and rewrite it using only expressions of the form not(a + b) or not a and not b.
    • Second approach: solve it graphically (more information will be provided in class)
    • Third approach: use the minterm/maxterm form and go from there.

Karnaugh Maps

  • After a quick introduction in class, reduce the following boolean functions to their simplest forms
    • f( a, b, c ) = &Sigma' ( 0, 1, 2, 3, 7 )
    • g( a, b, c, d ) = &Sigma' ( 0, 1, 2, 3, 7, 8, 10, 12, 13, 14, 15 )
    • h( a, b, c, d ) = &Sigma' ( 0, 1, 5, 6, 7, 11, 12, 14, 15 )
    • i( a, b, c, d ) =Π ( 2, 3, 14 )
    • j( a, b, c, d, e ) = Σ ( 0, 1, 2, 3, 7, 8, 12, 13, 14, 15, 16, 17, 18, 24, 28, 29, 30, 31 )

Majority Voter

  • A majority voter is a circuit receiving 3 inputs and comparing them, and reporting as output the majority of the three inputs. When 2 or 3 inputs are 1, the circuit outputs 1. When 2 or 3 inputs are 0, it outputs 0. In cases when one of the inputs is different from the other 2, the majority voter will output 2 bits representing the index of the wrong input.

For example, assume the 3 inputs are labeled b0, b1, and b2. If b0=0, b1=1, and b2=0, the voter will output 0, because 2 inputs are outputting this value, and the index of the wrong input is 01, corresponding to the index of b1.

  • Implement the majority voter with ANDs, ORs, and inverters, and XORs if necessary.
  • Implement it with NANDs only.
Retrieved from "http://dominiquethiebaut.com/dftwiki3/index.php?title=CSC270_Exercises:_Karnaugh_Maps,_Nands,_Nors&oldid=10281"