CSC270 Exercises: Karnaugh Maps, Nands, Nors 2012

--D. Thiebaut 14:43, 5 February 2012 (EST)

---

NANDs and NORs

• For this exercise, implement the circuit equivalent to the one shown below with NOR gates only.
  
  
  
  
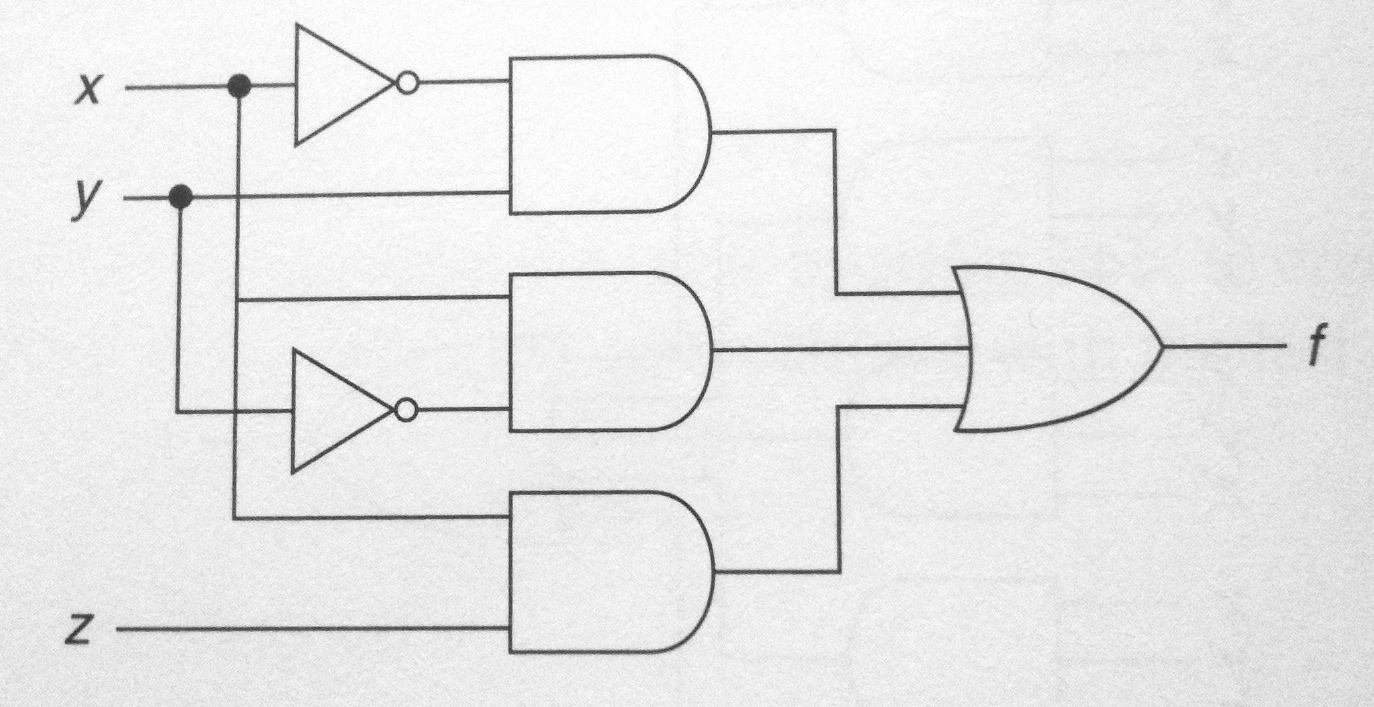
  • First approach: find the boolean expression for the output, and rewrite it using only expressions of the form not(a + b) or not a and not b.
    
  • Second approach: solve it graphically (more information will be provided in class)
    
  • Third approach: use the minterm/maxterm form and go from there.

Karnaugh Maps

• After a quick introduction in class, reduce the following boolean functions to their simplest forms

• • f( a, b, c ) = Σ ( 0, 1, 2, 3, 7 )

• • g( a, b, c, d ) = Σ ( 0, 1, 2, 3, 7, 8, 10, 12, 13, 14, 15 )

• • h( a, b, c, d ) = Σ ( 0, 1, 5, 6, 7, 11, 12, 14, 15 )

• • i( a, b, c, d ) =Π ( 2, 3, 14 )

• • j( a, b, c, d, e ) = Σ ( 0, 1, 2, 3, 7, 8, 12, 13, 14, 15, 16, 17, 18, 24, 28, 29, 30, 31 )

GRE Question

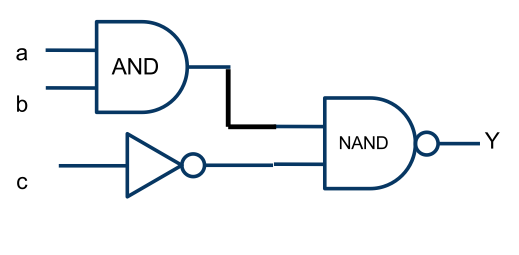
• What equation is implemented by the circuit above?
  • (1) a' + b' + c
  • (2) a.b + a.c
  • (3) a' . b' . c'

Majority Voter

• A majority voter is a circuit receiving 3 inputs and comparing them, and reporting as output the majority of the three inputs. When 2 or 3 inputs are 1, the circuit outputs 1. When 2 or 3 inputs are 0, it outputs 0. In cases when one of the inputs is different from the other 2, the majority voter will output 2 bits representing the index of the wrong input.

For example, assume the 3 inputs are labeled b0, b1, and b2. If b0=0, b1=1, and b2=0, the voter will output 0, because 2 inputs are outputting this value, and the index of the wrong input is 01, corresponding to the index of b1.

• Implement the majority voter with ANDs, ORs, and inverters, and XORs if necessary.

• Implement it with NANDs only.