CSC103 Homework 2 Fall 2012
--D. Thiebaut 06:13, 27 September 2012 (EDT)
This homework is due on 10/4/12 at 9:00 a.m.
Problem #1: A majority voter circuit
One circuit that is often found inside computing system is a majority voter. A majority voter is a circuit made of AND, OR and NOT gates that has 3 inputs and one output. The output is always the representation of the majority of the inputs. For example, if two or more of the inputs are 0, then the output is 0. If two or more of the inputs are 1, then the output is 1.
The truth table for such a circuit is shown below. the symbols a, b, and c represent input signals, while y is the output.
| inputs | output | ||
|---|---|---|---|
| a | b | c | y |
| 0 | 0 | 0 | <center>0 |
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | |
</center>
- Question 1
- What is the boolean expression for y? Express it as a follows:
y = ( (not a ) and ...
- and fill up the rest with not, and, or, a, b, and c.
- Question 2
- Convert your expression into a circuit containing logic gates. Draw it by hand (or with a computer drawing program, if you prefer).
- Question 3
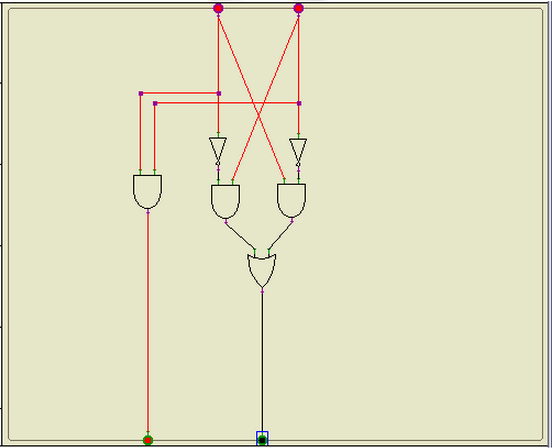
- Implement your circuit with the logic gate simulator we used in the lab on 9/27/12. Verify that your circuit behaves according to the truth table given above.
- Make a screen copy of your simulator window showing all the gates and the wiring, print it, and submit it with your homework. Below is an example of the type of image I would like you to submit: