CSC270 Homework 1
(c) --D. Thiebaut 22:01, 28 January 2009 (UTC)
Back to Main Page
This assignment is due on Wednesday evening, at the beginning of Lab 2.
Problem 1
Assume that we define a Boolean Algebra where the two values possible are { α, β }, and where the operators are U, T, and NOT.
The U operator has the following truth table:
| x | y | x U y |
|---|---|---|
|
α |
α |
α |
|
α |
α |
α |
|
α |
α |
α |
|
α |
α |
β |
The T operator has the following truth table:
| x | y | x T y |
|---|---|---|
|
α |
α |
α |
|
α |
α |
β |
|
α |
α |
β |
|
α |
α |
β |
Which of these assertions is true?
- α is 1, β is 0, U is the AND operator, and T the OR operator
- α is 0, β is 1, U is the OR operator, and T is the AND operator
Be sure to explain why one assertion is true, or why it is false!
Exercise #2
Expand and simplify the function defined as f(a, b, c, d ) = Σ(0, 1, 2, 8, 10, 12, 13, 14, 15)
Exercise #3
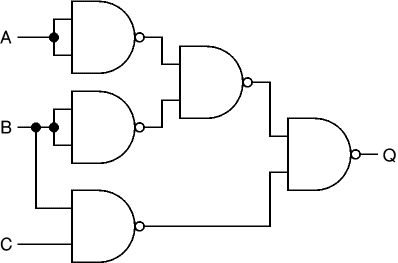
- What is the function f( A, B, C ) implemented by the circuit shown to the right, where the gates are NAND gates (an AND gate combined with a NOT gate on its output)?
- What is the minterm canonical form of f?