CSC111 Lab 13 2015b

--D. Thiebaut (talk) 20:44, 6 December 2015 (EST)

---

Visualizing Recursive Factorial At Work

Create a copy of this simple example:

# factorial.py
# Demonstrates a recursive factorial function

def fact( n ):
    # stopping condition
    if n<=1: 
        return 1

    # recursive step
    y = fact( n-1 )
    result = n * y
    return result


def main():
    n = int( input( "Enter a positive number: " ) )
    x = fact( n )
    print( "the factorial of %d is %d." % ( n , x ) )

main()

• Run your program
• It will prompt you for a number and will return its factorial.
• Verify that it computes the correct result. Below are some factorials numbers to compare your output to.

  1! =                    1
  2! =                    2
  3! =                    6
  4! =                   24
  5! =                  120
  6! =                  720
  7! =                 5040
  8! =                40320
  9! =               362880
 10! =              3628800
 11! =             39916800
 12! =            479001600
 13! =           6227020800
 14! =          87178291200

Visualizing, Step 1

• Add print statements to your fact() function so that it will let you know exactly what it does. For example, before it tests to see if n is less than equal to 1, you could print:

     print( "fact function started.  Receives n =", n )
     print( "testing if %d is >= 1" % (n) )

• Add print statements that will show the values of y and result.

• Run your program and observe its output. Can you see better how the function fact() recursively calls itself?

Visualizing, Step 2

• Create the more sophisticated program shown below. Observe it well first, and try to figure out what the indent variable does.

# factorialPrint.py
# Demonstrates a recursive factorial function
 
def fact2( n, indent ):
    print( indent, "fact2(%d) started" % n )
    print( indent, "comparing %d to 1" % n )
    if n<=1: 
        print( indent, "%d is <= 1.  Returning 1" % 1 )
        return 1

    print( indent, "%d is not <= 1.  Calling fact2(%d) and storing it in y" % (n, n-1) )
    y = fact2( n-1, indent + "    "  )
    print( indent, "just received %d from fact2( %d )." % ( y, n-1 ) )
    result = n * y
    print( indent, "multiplied %d by %d.  It's %d.  Returning %d to caller" % ( n, y, result, result ) )
    return result
 
 
def main():
    n = int( input( "Enter a positive integer: " ) )
    print( "Main calls fact( %d )" % n  )
    y = fact2( n, "   " )
    print( "Main receives result = ", y )
 
main()

• Run the program
• Explain the pattern made by the printed lines. Why this shape?
• Where does the stopping condition appear in the printed lines? In other words, where is the printed statement that indicates that fact() just received a value of n equal to 1? Why isn't this statement at the end of the printout?

Thinking Recursively

All the challenges below require you to put together a recursive function for a simple problem.

Thinking recursively is quite challenging and takes a while to master. So don't despair!

Here are points to remember when building a recursive function:

1. First, figure out what the function will return to the main program. Will it return a boolean? An integer? A list? Then when the function calls itself recursively, that's what it should expect to receive back from a call to itself.
   
   
2. What is the stopping condition? What is the smallest problem you can solve without recursion? That's the first thing you want to test for and do in your recursive function.
   
   
3. If the stopping condition doesn't apply, and the function has to do some work, figure out how to make one or several recursive calls to the function, get some intermediate results back, combine them together and get the final answer. That's the recursive step.
   

Challenge 1: Recursive Sum

• Given a number n, compute recursively the sum of all the numbers from 1 to n. For example, if you pass n = 5 to the solution function, it will return 15 (which is equal to 5+4+3+2+1)

Challenge 2: Recursive Even Sum

• Given a number n, compute recursively the sum of all the positive even numbers less than or equal to n.
• This is trickier than it seems! Here is an example of running a loop and asking the recursive function to compute the sum of all the even numbers up to n when n ranges from 0 to 12.

n = 0  sumEven(0) returns 0
n = 1  sumEven(1) returns 0
n = 2  sumEven(2) returns 2
n = 3  sumEven(3) returns 2
n = 4  sumEven(4) returns 6
n = 5  sumEven(5) returns 6
n = 6  sumEven(6) returns 12
n = 7  sumEven(7) returns 12
n = 8  sumEven(8) returns 20
n = 9  sumEven(9) returns 20
n = 10  sumEven(10) returns 30
n = 11  sumEven(11) returns 30

Recognizing Palindromes

A palindrome is a sentence that can be read forward and backward. For example "Able was I ere I saw Elba." Another one: "A man, a plan, a canal: Panama."

For this lab you are asked to write a function that is given a list, and that returns True if the list is a "palindromic", that is, if the list of items is the same scanning forward and scanning it backward. Below are example of lists that are "palindromic":

• [ 1, 10, 1 ]
• [ "hello", "hello" ]
• [ 1, "hello", "hello", 1 ]
• [ 1, 2, 10, -1, 10, 2, 1 ]

First, with your partner, generate a some lists that are not palindromes, and see what makes them so, compared to the lists above.

Explore several ways our collection of minions would do the work. You would give the whole list to a minion, who would be doing a tiny bit of work, then reduce the list, and possibly pass it on to another minion, who would do the same amount of work, etc, until one minion gets a list that is small enough that it can decided if it is a palindrome or not.

Write a program called lab13_1.py that contains a main program that takes different lists and tests wether they are palindromic using your recursive function.

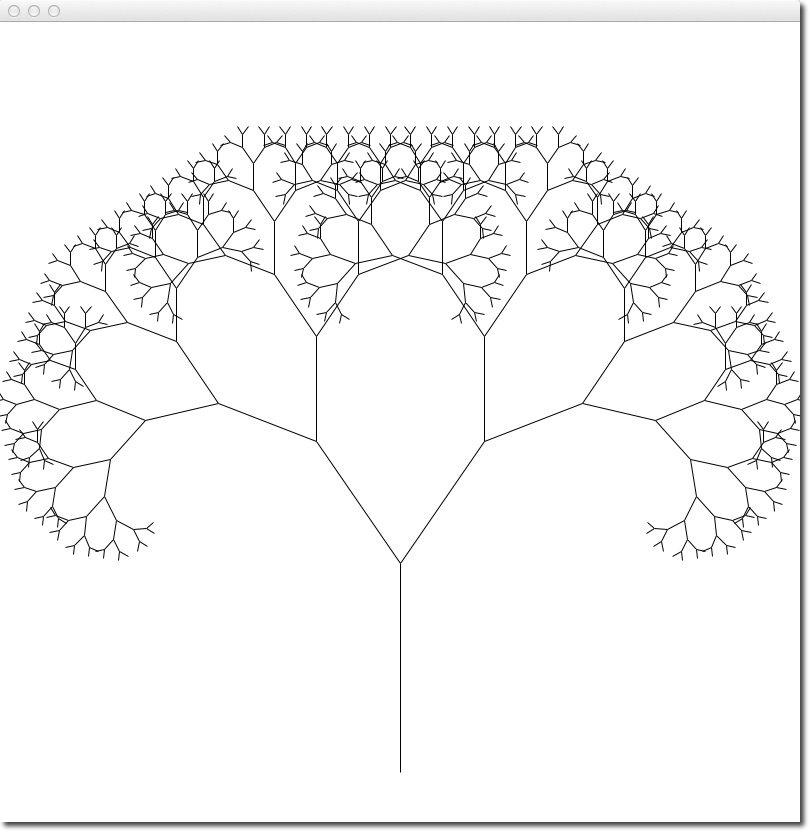
Fractal Trees

• This exercise is for you to explore recursion in the context of graphics.

• Create a new program with the code you'll find on this page, put it in the same directory where you store your graphics.py directory. You may want to call your program lab13_2.py.

• The program will generate a fractal tree. Fractals are self-similar objects: they look the same on a small scale as they do on a larger scale.

• Run the program first.
• Look at the code and see if you can figure out how the recursion works.
• To see how the different parameters influence the drawing of the fractal tree, modify the following parameters, one at a time, and give them different values:

theta

in the main program, change the angle theta which controls how much a branch will diverge from the direction of the branch that supports it. Try 0.4 first. Then try values between 0 and 0.8.

level of recursion

the main program passes 9 to the function as a starting level of recursion. Try passing smaller numbers first, then larger numbers (but less than 13 or so).

trunk_ratio

recursive function defines this as 0.29 and that represents the length of the trunk relative to its two branches. Try ratios between 0.1 (10%) and 0.9 (90%).