CSC231 Analysis of the Towers of Hanoi
--D. Thiebaut 16:24, 25 November 2012 (EST)
<showafterdate after="20151231 23:59" before="20300101 00:00">
Contents
A High-Level Version in Python
Bare Version
This version contains the bare minimum for the recursive solution to work. Try it out and play with it.
# hanoi.py (Python V 2.7)
# D. Thiebaut
# implements the game of hanoi in python.
# uses recursion.
#
# to run, type
# python hanoi.py
# at the command line
def moveDisk( source, dest, extra, n ):
if n==1:
print "move disk from %s to %s" % ( source, dest )
return
# more than 1 disk...
moveDisk( source, extra, dest, n-1)
print "move disk from %s to %s" % ( source, dest )
moveDisk( extra, dest, source, n-1)
def main():
while True:
n = input( "# of disks? " )
moveDisk( "A", "B", "C", n )
main()
Here's the output of small values of N:
# of disks? 1
move disk from A to B
# of disks? 2
move disk from A to C
move disk from A to B
move disk from C to B
# of disks? 3
move disk from A to B
move disk from A to C
move disk from B to C
move disk from A to B
move disk from C to A
move disk from C to B
move disk from A to B
# of disks? 4
move disk from A to C
move disk from A to B
move disk from C to B
move disk from A to C
move disk from B to A
move disk from B to C
move disk from A to C
move disk from A to B
move disk from C to B
move disk from C to A
move disk from B to A
move disk from C to B
move disk from A to C
move disk from A to B
move disk from C to B
Enhanced Version
The version below has been modified to illustrate the recursive nature of the calls.
# hanoi.py (Python V 2.7)
# D. Thiebaut
# implements the game of hanoi in python.
# uses recursion.
#
# to run, type
# python hanoi.py
# at the command line
N = 0
# indent( n ): returns an indentation that is a multiple of the string "| "
# which illustrates the nesting of the recursive calls.
def indent( n ):
return (N+1-n)*'| '
# the recursive moveDisk function.
# Stopping condition: n==1, in which case we just move the disk
# Recursive step: move n-1 out of the way, move 1, move n-1 back
def moveDisk( source, dest, extra, n ):
print "%smoveDisk( %s, %s, %s, %d)" % ( indent(n), source, dest, extra, n )
if n==1:
print indent(n-1) + ( "%s --> %s" % ( source, dest ) )
return
# more than 1 disk...
moveDisk( source, extra, dest, n-1)
print indent(n-1) + ( "%s --> %s" % ( source, dest ) )
moveDisk( extra, dest, source, n-1)
def main():
global N
while True:
N = input( "# of disks? " )
moveDisk( "A", "B", "C", N )
main()
The output of the program for N=4 is shown below:
# of disks? 4
| moveDisk( A, B, C, 4)
| | moveDisk( A, C, B, 3)
| | | moveDisk( A, B, C, 2)
| | | | moveDisk( A, C, B, 1)
| | | | | A --> C
| | | | A --> B
| | | | moveDisk( C, B, A, 1)
| | | | | C --> B
| | | A --> C
| | | moveDisk( B, C, A, 2)
| | | | moveDisk( B, A, C, 1)
| | | | | B --> A
| | | | B --> C
| | | | moveDisk( A, C, B, 1)
| | | | | A --> C
| | A --> B
| | moveDisk( C, B, A, 3)
| | | moveDisk( C, A, B, 2)
| | | | moveDisk( C, B, A, 1)
| | | | | C --> B
| | | | C --> A
| | | | moveDisk( B, A, C, 1)
| | | | | B --> A
| | | C --> B
| | | moveDisk( A, B, C, 2)
| | | | moveDisk( A, C, B, 1)
| | | | | A --> C
| | | | A --> B
| | | | moveDisk( C, B, A, 1)
| | | | | C --> B
Assembly Top-Down Approach: Version 1
Source
In this version all we do is simply set a main program that calls the function moveDisks and passes it
- the number of disk to move (in al)
- the source peg (in bl)
- the destination peg (in cl)
- and the extra or temporary peg (in dl)
The moveDisks function prints a single move, testing the printMove function that prints "X Y" on a line by itself, indicating that a disk must be move from X to Y.
Output
[231a@beowulf ~/handout]$ nasmld hanoi1 A --> B
Top Down Version 2
In this version we fully flesh out the recursive function. It would be hard to go half way with the implementation of moveDisks.
Source
Note here that we are using a macro, N, defined by the %define statement. This method of defining a constant is interesting as it allows us to modify the constant at assembly time.
Here's how.
- comment out the %define statement in the program (this will result in an undefined variable if we assemble as usual)
- when assembling the program, provide a value for the macro N as follows:
nasm -f elf -F stabs -dN=4 hanoi2.asm ; ld -melf_i386 -o hanoi2 hanoi2.o ; ./hanoi2
- The result will be that your program will be assembled just as if you had included the line
%define N 4
- inside your program.
The section below shows how to make the program run for several values of N:
Output
[231a@beowulf ~/handout]$ nasm -f elf -dN=2 -F stabs hanoi2.asm ; ld -melf_i386 -o hanoi2 hanoi2.o ; ./hanoi2
A C
A B
C B
[231a@beowulf ~/handout]$ nasm -f elf -dN=3 -F stabs hanoi2.asm ; ld -melf_i386 -o hanoi2 hanoi2.o ; ./hanoi2
A B
A C
B C
A B
C A
C B
A B
[231a@beowulf ~/handout]$ nasm -f elf -dN=4 -F stabs hanoi2.asm ; ld -melf_i386 -o hanoi2 hanoi2.o ; ./hanoi2
A C
A B
C B
A C
B A
B C
A C
A B
C B
C A
B A
C B
A C
A B
C B
Trick
If we want to count the number of moves for a given number of disk, we can pipe the output of the ./hanoi2 program in the command wc, which stands for word-count. wc outputs the number of lines, number of words, and number of characters in the text given to it.
Below are the same commands as above, but filtered by wc:
[231a@beowulf ~/handout]$ nasm -f elf -dN=2 -F stabs hanoi2.asm ; ld -melf_i386 -o hanoi2 hanoi2.o ; ./hanoi2 | wc
3 6 12
[231a@beowulf ~/handout]$ nasm -f elf -dN=3 -F stabs hanoi2.asm ; ld -melf_i386 -o hanoi2 hanoi2.o ; ./hanoi2 | wc
7 14 28
[231a@beowulf ~/handout]$ nasm -f elf -dN=4 -F stabs hanoi2.asm ; ld -melf_i386 -o hanoi2 hanoi2.o ; ./hanoi2 | wc
15 30 60
We see that the number of moves for 2 disks is 3, for 3 disks it's 7, for 4 disks it's 15, for n disks, it's 2n-1.
Estimating the Execution time
Call Tree of MoveDisks( 4, 'A', 'B', 'C' )
N, Source, Dest, Extra
4,A,B,C
|
+---------------------------+-------------------------------+
| | |
3,A,C,B 1,A,B,C 3,C,B,A
| |
+-------------+------------+ +------------+-------------+
| | | | | |
2,A,B,C 1,A,C,B 2,B,C,A 2,C,A,B 1,C,B,A 2,A,B,C
| | | |
+--------+--------+ +--------+--------+ +--------+--------+ +--------+--------+
| | | | | | | | | | | |
1,A,C,B 1,A,B,C 1,C,B,A 1,B,A,C 1,B,C,A 1,A,C,B 1,C,B,A 1,C,A,B 1,B,A,C 1,A,C,B 1,A,B,C 1,C,B,A
| | | | | | | |
1,A,C,B 1,C,B,A 1,B,A,C 1,A,C,B 1,C,B,A 1,B,A,C 1,A,C,B 1,C,B,A
Let's look at the top two levels of the tree:
4,A,B,C
|
+---------------------------+-------------------------------+
| | |
3,A,C,B 1,A,B,C 3,C,B,A
| |
We read it as follows.
- MoveDisks is called to move 4 disks from A to B, using C as an extra peg. To do so it calls itself once to move 3 disks from A to C, to put them "out of the way", and uses B as a temporary peg to do so. Then it moves 1 disk from A to B. Then it has to move the 3 disks that were on C back to B where the belong, and it uses A as an extra peg in the process.
Estimating the Number of Instructions Executed
Let's figure out how many instructions are executed by the different parts:
| Tree part | Number of instructions |
|---|---|
|
4,A,B,C |
Start function: 4 pushes + 1 cmp + 1 jump = 6 |
|
3,A,C,B |
Start recursion: 1 dec, 2 xchng, 1 call = 4 |
|
1,A,B,C |
Print 1 move: 6 instructions + printMove code = 6 + 7 + int 80 |
|
3,C,B,A |
Start 2nd recursion: 1 xchang, 1 call, 4 pops, 1 ret = 7 |
We can see that we can figure out the number of instructions accurately except for the int 0x80 instruction which is a total unknown. We have no idea how many instructions Linux is executing to print the string on the screen. So let's just comment out this instruction and see what we get.
N, Source, Dest, Extra
4,A,B,C
|6
+---------------------------+-------------------------------+
|4 |13 |7
3,A,C,B 1,A,B,C 3,C,B,A
|6 |6
+-------------+------------+ +------------+-------------+
|4 |13 |7 |4 |13 |7
2,A,B,C 1,A,C,B 2,B,C,A 2,C,A,B 1,C,B,A 2,A,B,C
|6 |6 |6 |6
+--------+--------+ +--------+--------+ +--------+--------+ +--------+--------+
|4 |13 |7 |4 |13 |7 |4 |13 |7 |4 |13 |7
1,A,C,B 1,A,B,C 1,C,B,A 1,B,A,C 1,B,C,A 1,A,C,B 1,C,B,A 1,C,A,B 1,B,A,C 1,A,C,B 1,A,B,C 1,C,B,A
|6 |6 |6 |6 |6 |6 |6 |6
1,A,C,B 1,C,B,A 1,B,A,C 1,A,C,B 1,C,B,A 1,B,A,C 1,A,C,B 1,C,B,A
9+7 9+7 9+7 9+7 9+7 9+7 9+7 9+7
Which simplifies to this:
+--------------( )--------------+ (6+4+13+7)x1
| | |
+------( )------+ +------( )------+ (6+4+13+7)x2
| | | | | |
+--( )--+ +--( )--+ +--( )--+ +--( )--+ (6+4+13+7)x4
| | | | | | | | | | | |
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (6+9+7)x8
| | | | | | | |
The total number of instructions is approximately (6+4+13+7) x ( 1 + 2 + 4 + 8 ) = (6+4+13+7) x 15 = (30) x ( 24 - 1 )
The tree above is for N=4 disks. The expression above simplifies to 30 x ( 2N - 1 ) ≈ 30 x 2N.
Processor Approximation
We are now going to make an approximation about the Pentium, that it executes 1 instruction every cycle. Another performance measured by computer architects is CPI, or cycle per instruction, which in this case would also be equal to 1. Such an assumption is pretty safe with the current modern Pentium processors.
Speed of our Machine
To find the speed at which the processor on our machine (beowulf) is operating, we ask Linux:
cat /proc/cpuinfo processor : 0 vendor_id : AuthenticAMD cpu family : 15 model : 65 model name : Dual-Core AMD Opteron(tm) Processor 2222 SE stepping : 3 microcode : 0x6d cpu MHz : 2992.478 cache size : 1024 KB physical id : 0 ...
Beowulf's processor operates at 2.99 GHz. Its cycle time is thus 1/2.99E9 seconds.
Modeling with Excel
We now have all the data to predict the approximate execution time of our program for different values of N. We have created an eXcel table with the equation for the number of instructions as a function of N and multiplied by the cycle time:
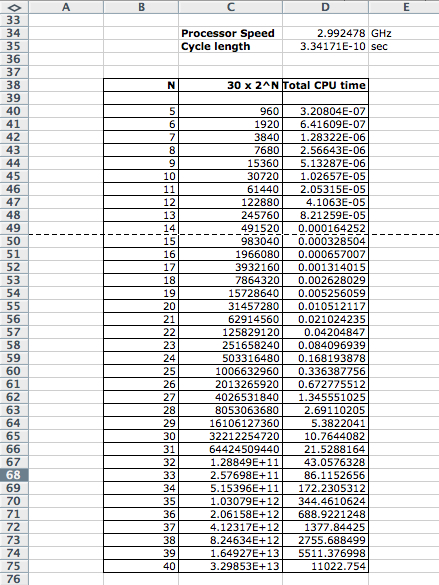
Verification
We notice in the table that the execution time passes the 1-second threshold around N=26, N=27.
Let's try these two values of N with our program:
[231a@beowulf ~/handout]$ nasm -f elf -dN=26 -F stabs hanoi2.asm ; ld -melf_i386 -o hanoi2 hanoi2.o ; /usr/bin/time -p ./hanoi2 real 1.01 user 1.00 sys 0.00 [231a@beowulf ~/handout]$ nasm -f elf -dN=27 -F stabs hanoi2.asm ; ld -melf_i386 -o hanoi2 hanoi2.o ; /usr/bin/time -p ./hanoi2 real 2.11 user 2.11 sys 0.00
We see that the amount of user time, i.e. the amount of processor time given to the user's process (the hanoi2 program) is 1.00 second for N=26 and 2.11 seconds for N=27. The spreadsheet predicted 0.67 sec and 1.3 sec. We are undershooting the real execution times by less than a factor of 2. If better accuracy is required, we can go back and refine our oversimplifying model to get a closer estimate. But for today, less than a factor of 2 away from the real time is fine.
End of the World
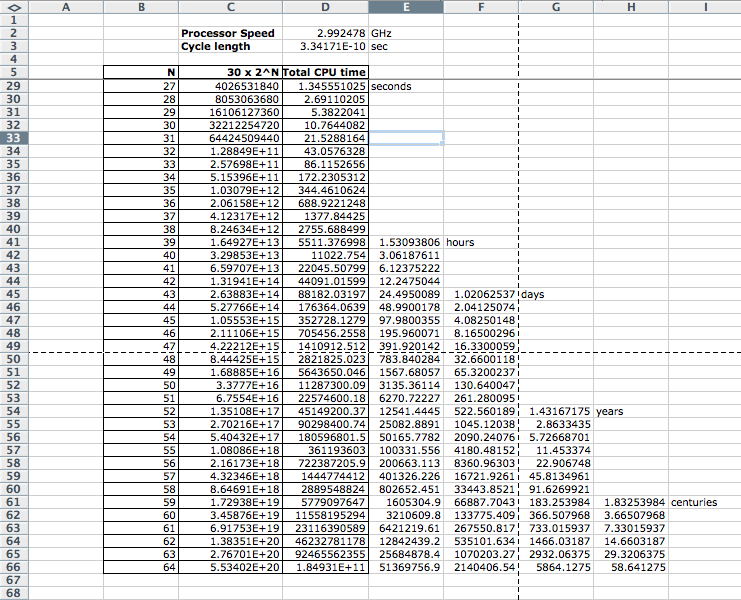
The legend associated with the Towers of Hanoi is that when it was discovered, this game was being played by monks who were moving 64 disks from one peg to another. The monks knew that by the time they had moved the last disk, the world would have ceased to exist. The spreadsheet shows how long our model predict our pentium processor to take for computing the moves required by a tower of 64 disks:
Cutting the tail-end recursion
One way to make recursive program faster is to somehow prune the recursion tree and remove either branches or levels. With Hanoi we can easily remove the lower level of the tree by cutting the recursion when n==2, instead of n==1. The python program below illustrates what this would look like.
# hanoi3.py (Python V 2.7)
# D. Thiebaut
# implements the game of hanoi in python.
# uses recursion and some of the tail recursion
# trimmed at N==2
#
# to run, type
# python hanoi.py
# at the command line
count = 0
def moveDisk( source, dest, extra, n ):
global count
if n>2:
# more than 2 disks...
moveDisk( source, extra, dest, n-1)
print "move disk from %s to %s" % ( source, dest )
count += 1
moveDisk( extra, dest, source, n-1)
elif n==2:
print "move disk from %s to %s" % ( source, extra )
print "move disk from %s to %s" % ( source, dest )
print "move disk from %s to %s" % ( extra, dest )
count += 3
else: # n == 1
print "move disk from %s to %s" % ( source, dest )
count += 1
def main():
global count
while True:
count = 0
n = input( "# of disks? " )
moveDisk( "A", "B", "C", n )
print count, "moves..."
main()
</showafterdate>