CSC103 Logic Lab 2017

--D. Thiebaut (talk) 11:45, 19 September 2017 (EDT)

---

<meta name="keywords" content="computer science, How Computers Work, Dominique Thiebaut, smith college" /> <meta name="description" content="Dominique Thiebaut's Web Page" /> <meta name="title" content="Dominique Thiebaut -- Computer Science" /> <meta name="abstract" content="Dominique Thiebaut's Computer Science Web pages" /> <meta name="author" content="thiebaut at cs.smith.edu" /> <meta name="distribution" content="Global" /> <meta name="revisit-after" content="10 days" /> <meta name="copyright" content="(c) D. Thiebaut 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007,2008" /> <meta name="robots" content="FOLLOW,INDEX" />

Back to CSC103 Main Page

This lab is about logic design. Work in pairs and alternate with your lab partner when working at the keyboard. You do not have to turn in anything at the end of the lab. The goal of the lab is to get you to play with a logic gate simulator.

Logic Simulator

Reference

• We will be using LOGIC.LY's simulator for this lab. It's a superior simulator with a very natural interface.
• You can find a nice description of the simulator used in this lab at https://logic.ly/help/?utm_source=logicly-demo&utm_content=menu-help

The Simulator

1. Go to logic.ly to start the simulator

NOT, OR, and AND gates

Study all three fundamental gates: the NOT gate, the OR gate, and the AND gate.

The NOT gate

1. Drag a Toggle Switch symbol from to the top-left section of the menu to the wiring area. Position it to the left. This will be your input.
2. Drag a Light Bulb symbol on the rightmost part of the wiring area. Position it to the right. This will be your output.
3. Drag a NOT gate from the Logic Gates area to the middle of the area.
4. Connect the switch to the input of the NOT gate with a wire (left click and drag), and the output of the NOt gate to the light bulb with another wire.
5. Click on the switch symbol to generate a 1 (blue color) or a zero (white). Try all possible variations of the input and verify that the output value is always the opposite of the input value.
   
   Remember that you can drag symbols around to reposition them, if necessary.

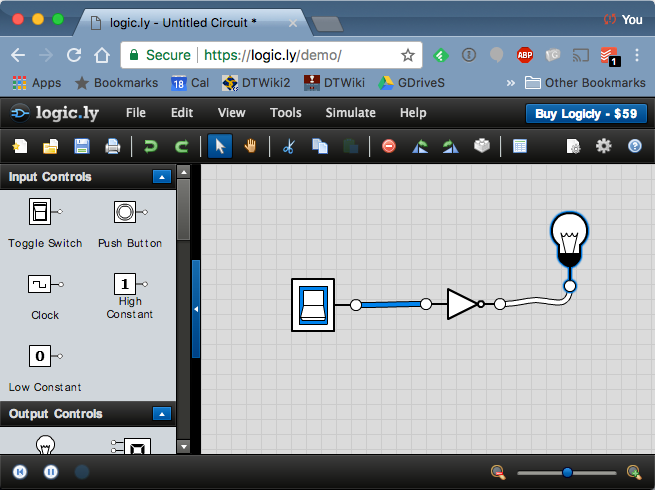
Once you're done, clear your wiring area and wire up an OR gate, as shown below:

The OR gate

• Take the similar steps as you did for the NOT gate, and wire up an OR gate with 2 inputs (you will be asked for the number of inputs when you drag the symbol to wiring area).
• Add a label (very bottom part of the left menu of symbols) above each of the two switches, and above the light bulb.
• Add wires between the switches and the inputs of the gate.
• Add a wire between the output of the gate and the light bulb.
• Try all possible combinations of the two inputs and verify that it's truth table is the following one:

a	b	a OR b
0	0	0
0	1	1
1	0	1
1	1	1

The AND gate

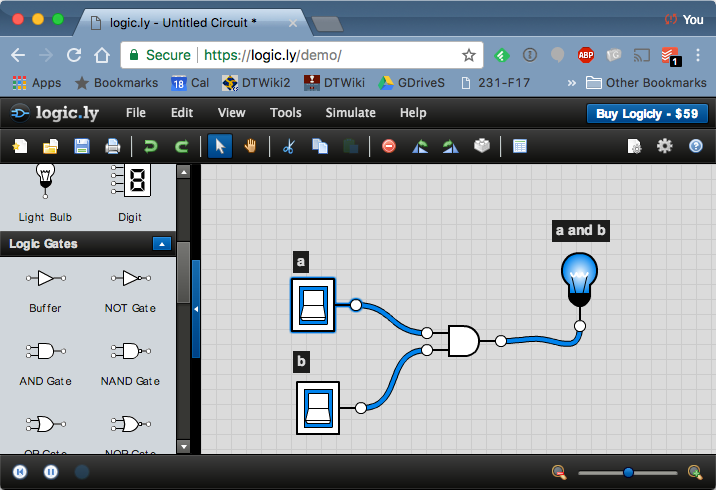
Take the similar steps as you did for the OR gate, and wire up an AND gate with 2 inputs. Try all possible combinations of the two inputs and verify that it's truth table is the following one:

a	b	a AND b
0	0	0
0	1	0
1	0	0
1	1	1

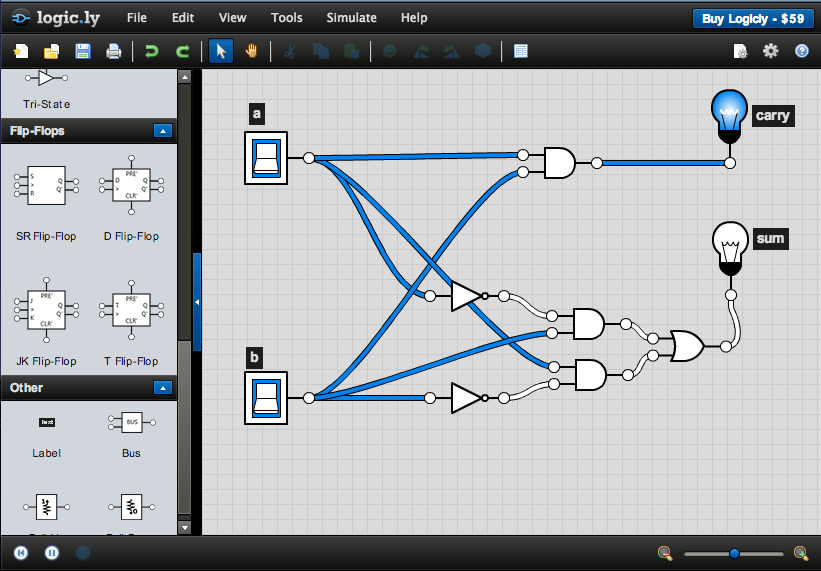
Binary Adder

Wire up the circuit of the binary adder which we have seen in class.

Try all possible combinations of the inputs, and verify that the outputs correspond to the sum of the two inputs, in binary.

a	+	b	=	carry		sum
0	+	0	=	0		0
0	+	1	=	0		1
1	+	0	=	0		1
1	+	1	=	1		0

Submission

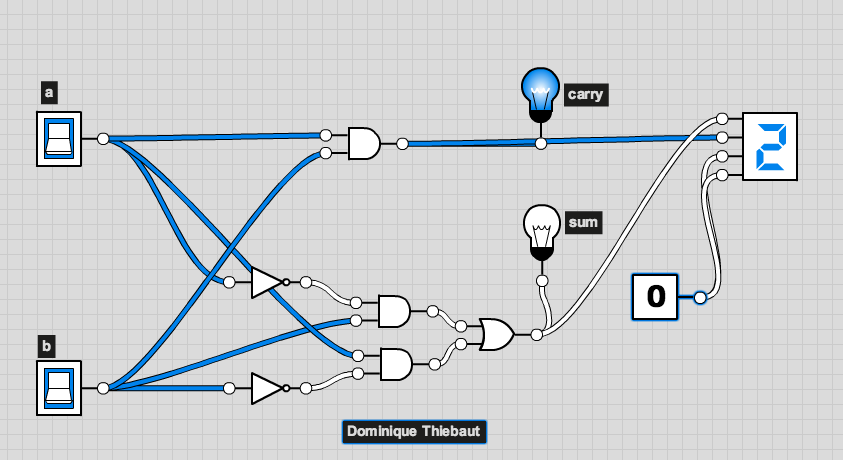
• When you are done with a design for the binary adder that works, add a text label in the lower part of the wiring areal, with your name (and that of your lab partner), as illustrated in the image below (I used my name for this example):

• Take a screen capture of your design (limit it to just the wiring area if possible) and submit that image to Moodle, in the Logic Design Lab section.

3-Bit Adder (Optional)

• A 3-bit adder is a circuit with 3 inputs, or bits, and two outputs, corresponding to the carry and the sum, as for the 2-bit adder.

• On a piece of paper, write the truth table for the 3-bit adder.

b1	b2	b3	carry	sum
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

• Generate the boolean equations (using a, b, c, AND, OR and NOT) for the sum and the carry.

• Use the simulator to verify that the logic expression for the carry bit can also be realized by a different equation, very likely shorter than the one you found (there can be many equations that result in the same behavior):

         carry  =  ( a AND b ) OR ( a AND c ) OR ( b AND c )

• Once you have wired and tested it, demonstrate it to your instructor! :-)

Hope you enjoyed the lab!