CSC212 Lab 10 2014
--D. Thiebaut (talk) 22:52, 28 October 2014 (EDT)
Contents
- 1 Generating Graphic Representations of Trees
- 2 Binary-Search Trees
- 3 Debugging With Eclipse
This lab deals with Binary Search Trees. The last part of the lab introduces you to Eclipse in debugging mode. Even if you do not have time today to go through this last section, make sure you do during the week, as it will be a very useful tool for you in future assignments.
Generating Graphic Representations of Trees
Graphviz is a simple engine for generating very polished images of trees or graphs. Graphviz takes the definition of a tree, or of a graph, written in a specific language called DOT and produces images of the tree or graph structure. Graphviz is sometimes installed on Linux systems, and can be installed as well on Windows and Mac computers. See the see Graphviz's Download page for more details. But, if graphviz is not installed on the computer you are using, there are several on-line graphviz editors we can use.
Let's generate a simple Tree.
- Open this page in your browser: http://graphviz-dev.appspot.com/ (if the site is down, try this one instead: http://sandbox.kidstrythisathome.com/erdos/
- Make sure DOT is selected as the language
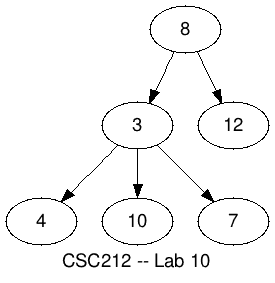
- Enter the following graph definition in the Edit window.
digraph "Lab10" {
label = "CSC212 -- Lab 10";
8 -> 3;
3 -> 4;
3 -> 10;
3 -> 7;
8 -> 12;
}
- As you type, you should see a graph appearing in the right window.
Challenge 1: Create A Binary-Search Tree |
- Use the same utility to create the tree used in the lecture slides, and shown below (this tree image was not generated with graphviz, but taken from the Wikipedia page on trees):
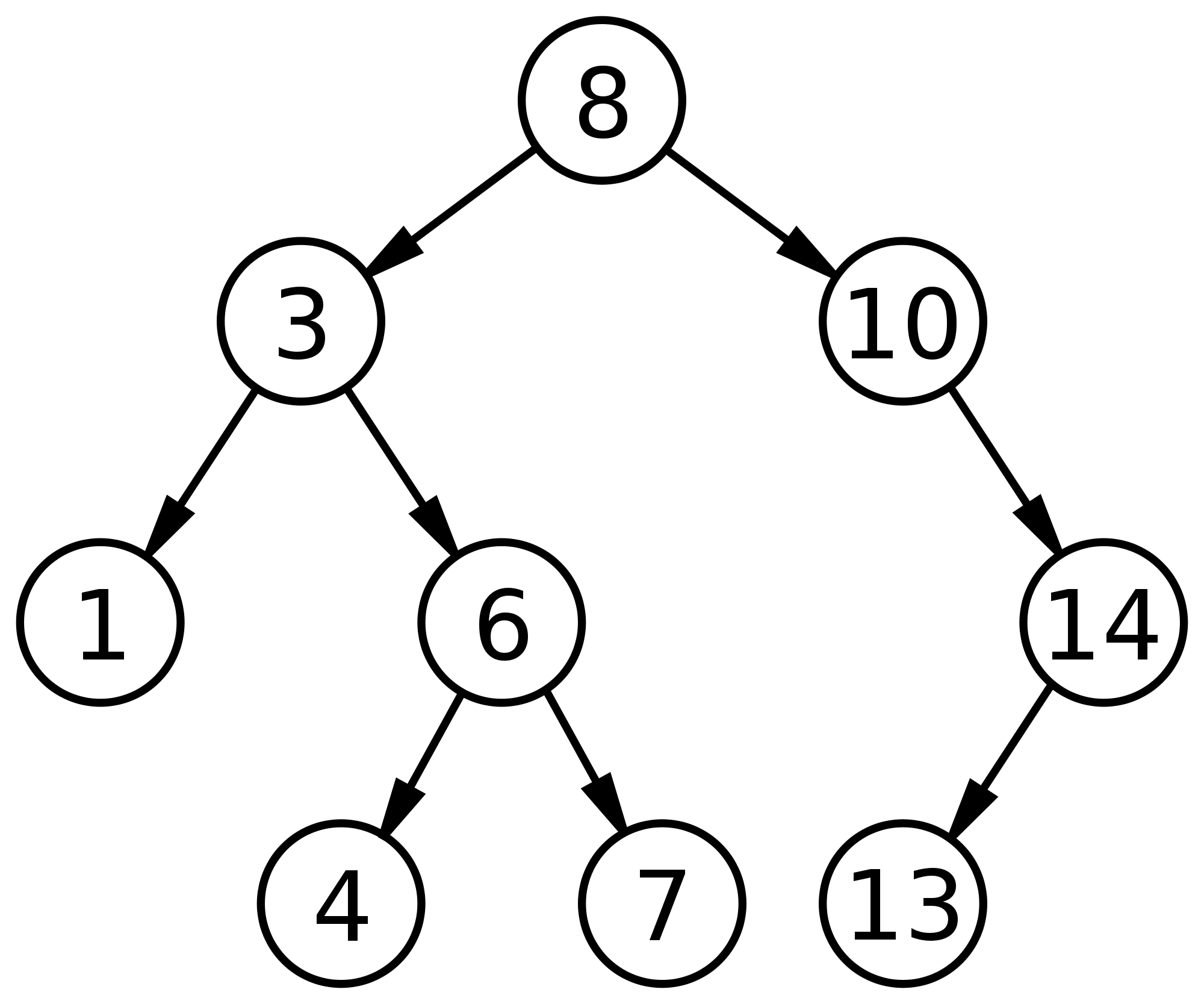
- You will notice that your graphviz tree doesn't display well when a node only has 1 child. To get a more accurate left-right balance of the nodes, we simply need to create "fake" nodes for the null pointers.
Adding "Fake" Null Nodes
The two nodes that do not display well are 10 and 14 because they have only 1 child each. To prevent the vertical alignment, we can declare them as follows, in the DOT language:
digraph "Lab10" { label = "CSC212 -- Lab 10"; 8 -> 3; 8 -> 10; 3 -> 1; 3 -> 6; 6-> 4; 6 -> 7; null10left [shape=point]; 10 -> null10left; 10 -> 14; 14 -> 13; null14right [shape=point]; 14 -> null14right; }
- Go ahead and enter the new definition for the tree. Observe that it is now correctly oriented.
The Dot Language
- You have just learned a new language! DOT.
- DOT is quite rich, and will allow you to generate more sophisticated trees (or graphs) than we have done in this lab, and you can see some examples of graphs here: http://www.graphviz.org/Gallery.php.
- If you are interested in learning more about the Dot language for generating trees or graphs with graphviz, you may want to read this Wikipedia page on the Dot Language, or this very nice guide, available here.
Binary-Search Trees
- Get the code for the BST Tree from this page.
- Run it.
- It should create the tree used in the class lectures, shown below. Eclipse does not generate graphics, though, so you only see text output, listing all the nodes traversed by debugVitit() search.

Visiting The Tree
- Modify the main() function of your IntBST class and display the contents of the your tree using
- the breadth-first visit function.
- Verify that the output of the function is correct.
- Same exercise, but this time use the following methods. For each one, make sure you read the code of the function first to understand how it will operate. Then run the code.
- the inOrder() visit function.
- the preOrder() visit function.
- the postOrder() visit function.
Counting the Number of Nodes
- Let's count the number of nodes in the tree. Currently, the class does not have any support for counting the number of nodes, so you will need to modify the code.
- Step 1: add a new int member variable called counter at the top of the class, before the constructor.
- Step 2: pick the visiting method of your choice ( breadthFirst, inOrder, preOrder, postOrder ) and make a copy of it. Call the copy countNodes() (or something similar).
- Step 3: modify countNodes so that it increments counter every time it visits a valid node.
- Add some code to your main() function that will call countNodes(), get the value it returns, and display that value on the screen.
- Make main() go through the computation and display oif the number of nodes twice, to make sure that you reset the counter correctly from inside the function countNodes(). Resetting the counter in main() is not acceptable; you don't want a program using the tree to have to reset some counter before it uses a method that returns the number of elements in the tree! So your function has to reset the counter when it starts.
Computing the Height of the Tree
- Let's now compute the height of the tree. The height is defined as the number of nodes on the longest path from the root to a leaf. The height of the tree above is 4.
- One approach to compute the height is to use one of the visiting methods available (say inOrderVisit), make a copy of it, and modify it. The modified visit method works as follows:
- When it is called the first time, it starts recursing on the root and is given the number 0, representing the root's level of 0. Then when the visit method moves from the root to the children, it passes 1 to them as their level. Then these will pass 2 to their children. This way, when the visiting method visits a node, it knows the level of the node. It can then simply compare that level to a member variable (global) where we keep track of the largest level seen so far.
- When the visit is done, the largest level + 1 is the height.
- Here's a skeleton of how this will work (the code is incomplete, you will have to add code here and there):
public int computeHeight( ) { // set the maxLevel member variable to 0 ... // start recursing on the root computeHeight( root, 0 ); // when we come back, the maxHeight will have been set return maxLevel + 1; } private void computeHeight( IntBSTNode p, int level ) { // if p is a valid node, and if the height is greater than maxLevel, // then update maxLevel with current height. // recurse on the left and right children, and pass level+1 to both. computeHeight( /* left child */, level + 1 ); computeHeight( /* right child */, level + 1 ); }
- Try making it work!
Submission to Moodle
- Submit the IntBST.java code that contains the computeHeight() function to Moodle, in the Lab10 section.
Filling Up the Tree
Here's an example program that generates 20 random positive integers:
import java.util.Random; public class GenerateRandomInts { public static void main(String[] args) { Random randomGenerator = new Random(); // generate 20 random ints for (int idx = 0; idx < 20; ++idx){ // generate a positive random int int randomInt = Math.abs( randomGenerator.nextInt() ); System.out.println( randomInt ); } } }
Build a Tree of 32 Random Ints |
- Use the code above in some fashion, and fill up an empty tree with 32 random ints.
- Why 32, by the way?
- When you have a new number to add to the tree, make sure the number is not already in the tree before inserting it. We do not want duplicates in our tree. (So search for the number first, and if search returns null, you know the number isn't already there...)
- Once you're done, generate the GraphViz/DOT version of your tree, and display it in the on-line visualizer we used earlier.
- Run your program a couple more times, and every time visualize the tree that results. Observe how different the trees are...
Count the Number of Probes Used When Searching |
- Add a new counter to your tree class, say probeCounter, as a new member variable. You will use it to count how many probes are required to search for a key in the tree. Remember, probe for us means the action of looking at a key in a node.
- Modify your program so that, after it has inserted its 32 ints in the tree, it will insert the key 33 in the tree. This way there will be at least one number in the tree that you will know is there.
- Modify the program some more, and make it search for 10 different keys and display how many different probes it has to perform for each search. Here's a skeleton of what you have to do:
int N = 32; for ( int i=0; i < N; i++ ) { // insert unique random int in tree... } // insert a key we know tree.insert( 3300000 ); // pick 10 keys we're going to search for, including 33, which should result in a successful search... int[] keys = new int[] { 17905000 , 3111463, 3300000, 60600000, 8989000, 869000004, 1769211540, 4000000, 269211540, 56891000 }; // search for each of the 10 keys and display # of probes... for ( int i=0; i < keys.length; i++ ) { IntBSTNode p = tree.search( keys[i] ); // get the number of probes int probes = tree.getNoProbes() // I'm assuming I/you have created such a method... System.out.println( "Searching for " + keys[i] + " required " + probes + " probes." ); }
- Go ahead and make it work!
- When your program works, make is also print whether the search was successful or not. Make sure that it reports success for 33!
- The theory says that we should perform, on the average, roughly log2(32) probes in order to locate a key. log2(32) is 5 (if you divide 32 by 2, then the result by 2, and continue repeatedly, you'll go 5 times, or log2(32) times, before you get down to 1). Do you see an average of 5 probes? Why or why not?
Filling up the Tree with 1,000,000 Random Ints |
- Repeat the previous experiment, counting search-related probes, when your tree contains 1 million random unique ints.
- log2(1000000) is approximately 20. Do you see an average of 20 probes?
- Why or why not?
Balancing the 1M-Node Tree |
- Same question as the previous one, but this time balance your tree once you have inserted the million nodes, and before you perform your 10 searches. The IntBST class contains a balance() method (along with several helper functions). Figure out how to use them.
- What's the average number of probes this time? Better than in the previous question? Why or why not?
Debugging With Eclipse
Part 1: Getting Started with the Eclipse Debugger
- Open Eclipse
- Create a New Java Class. Call it DebugDemo.
- Enter this code in it:
// DebugDemo.java // D. Thiebaut // CSC212 import java.util.ArrayList; import java.util.Iterator; class Pair { public String name; public int age; Pair( String f, int s ) { name=f; age=s; } public String toString() { return name+"("+age+") "; } } public class DebugDemo { public static void main(String[] args) { ArrayList<Pair> A = new ArrayList<Pair>(); int increment = 3; A.add( new Pair( "Alice", 10 ) ); A.add( new Pair( "Bob", 7 ) ); Iterator<Pair> it = A.iterator(); while ( it.hasNext() ) { Pair p = it.next(); p.age += increment; } for ( int i=0; i<3; i++ ) { Pair p = A.get( i ); System.out.println( A.get( i ) ); } } }
- Run it.
- Observe what the program does. It simply creates an array of 2 pairs, containing Alice(10) and Bob(7), and modify the age of both by an increment of 3.
Go into Debugging Mode
- In the Package Explorer tab (left tab), right/control click on DebugDemo and select Debug As and Java Application.
- The windows will reorganize themselves (if not, see below):
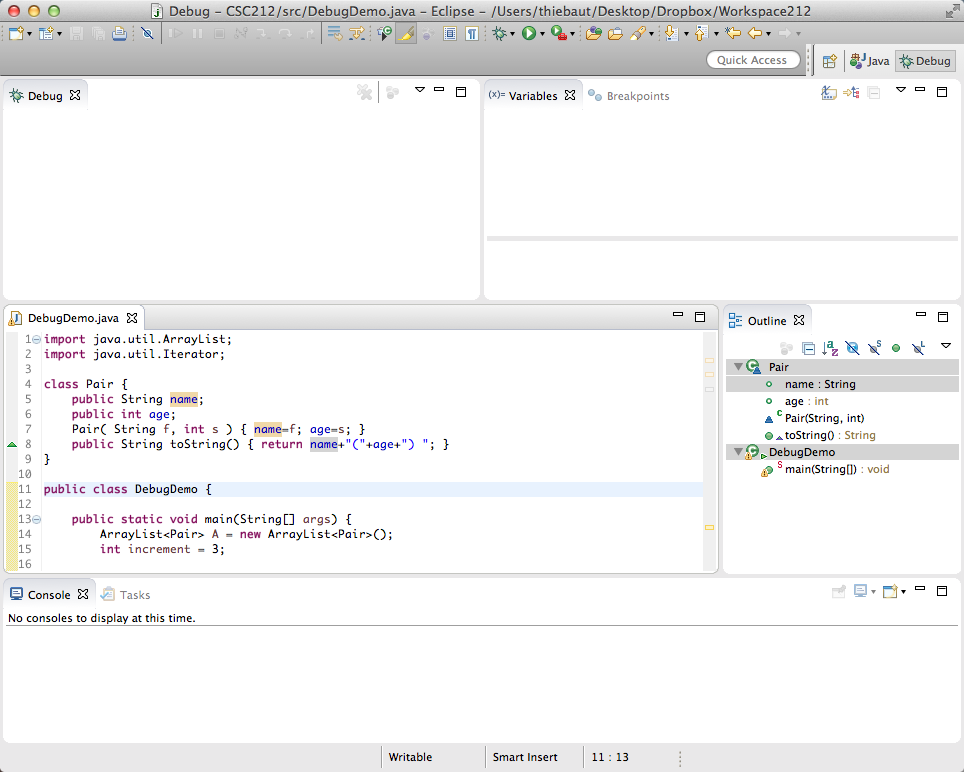
- If you do not get the window shown above, click on the little "table and plus symbol" in the top right of the window, and pick Debug in the new pop-up window :
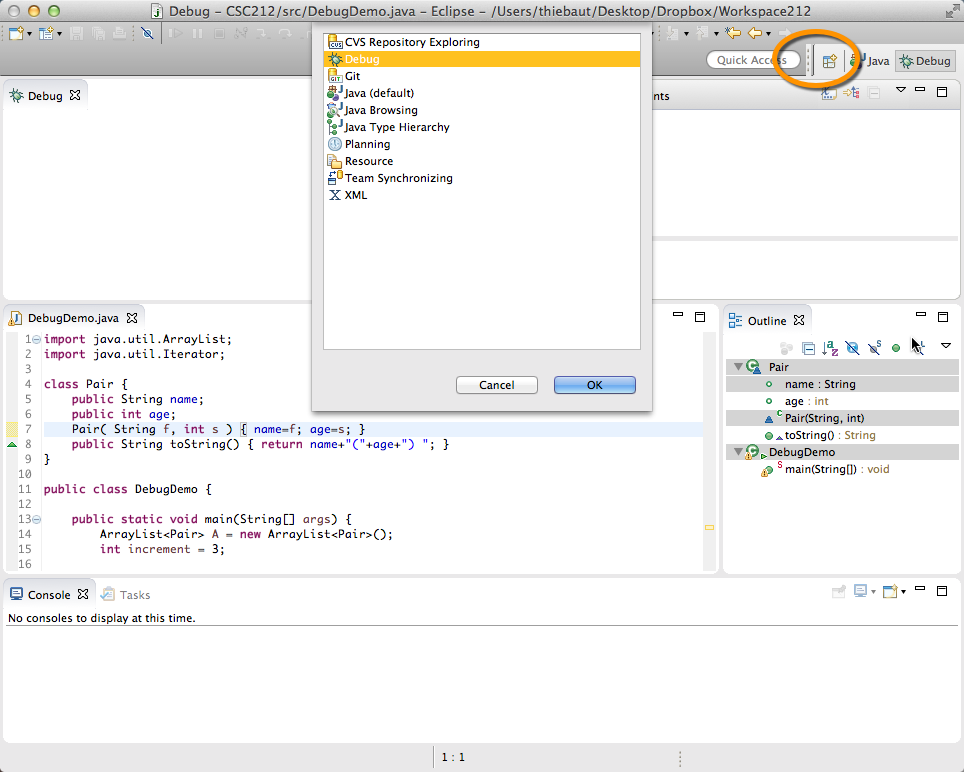
- You can switch back and forth between Java coding and debugging using the Java and Debug buttons in the top right of the Eclipse window.
Getting Ready to Debug
- One of the best method to start when debugging is to follow this 3-step approach:
- Set a breakpoint on a line of code where you want to start observing what your program is doing.
- Run your program full speed. As soon as the computer reaches the breakpoint, it will stop (but not exit), and wait for your instructions.
- Single-step your program, observing how the different variables and data structures evolve.
Set A Breakpoint
- We will want to start watching our program from the beginning of main, when the program puts the first pair in the array.
- Put your cursor in the 17 in the left margin of A.add( new Pair( "Alice", 10 ) );
- Right/Control click on 17.
- Select Toggle Breakpoint. A blue dot should appear left of 17.
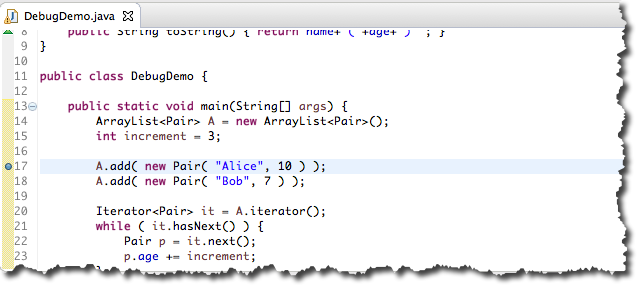
Run the Program to the Breakpoint
- Now that you have a breakpoint, you can run the program; it will automatically go through the initialization, and will stop on the breakpoint. It will not execute line 17, though. It will simply break on it.
- Click on the bug, next to the green circle with white arrow to start debugging the program.
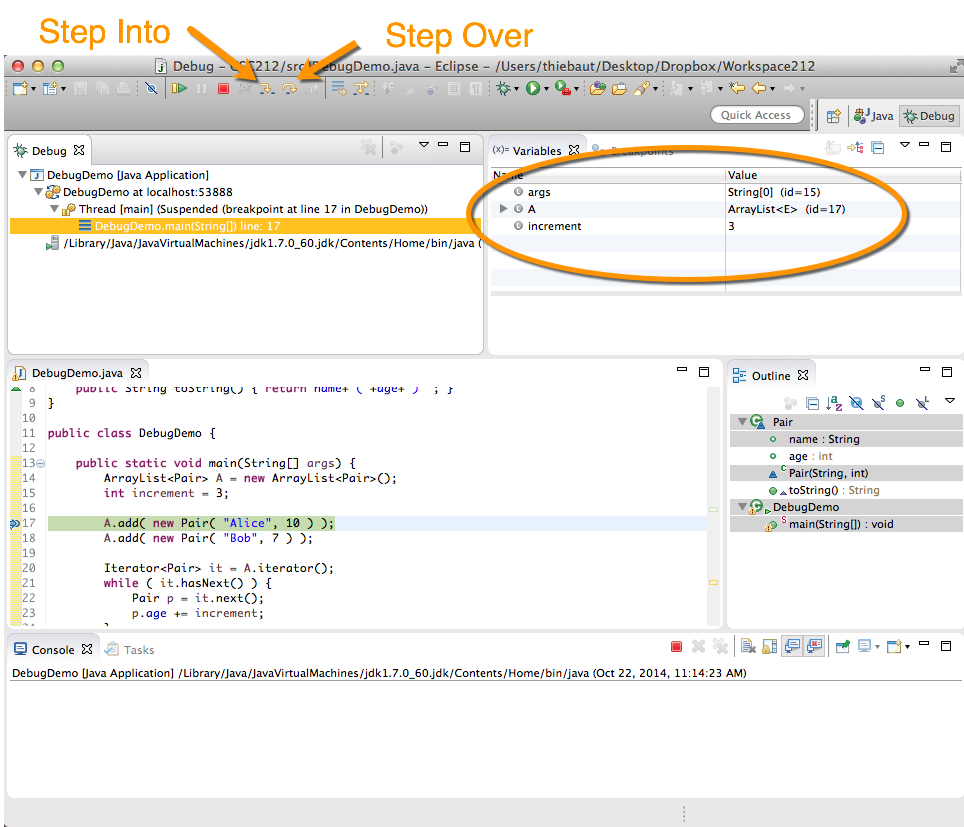
- Note several new pieces of information that have appeared
- The top-right tab called Variables shows you the local variables of the block you are in. Note that you see 3 variables, including args, A, and increment, along with their values.
- The top menu has 2 new active buttons, one for stepping into lines of code, one for stepping over lines of code. The difference is that Step into will take you inside functions that appear in the line of code you're debugging. Step Over will run the functions appearing in the current code line full speed. Most of the time, we want to use Step Over.
- Step Into an also be activated by the F5 key.
- Step Over by the F6 key.
Single Step
- Click Step Over or F6 once.
- Note that Line 18 is now highlighted. It is the next line Eclipse is ready to execute. It has finished Line 17.
- Click on the triangle next to the array A in the top right Variables window to open it.
- Click on the triangle next to elementData to see the elements of A.
- Click on the triangle nexxt to Element [0].
- Do you see Alice and her age of 10?
- You have just verified that Line 17 of your program added (Alice,10) to the array A.
- Click Step Over one more time. Verify that (Bob, 7) was added to A. Observe that all objects have an id. It makes it easy to identify things such as pairs, or strings.
- Click Step Over a few times until you reach Line 23. Observe that p points to a pair object, containing Alice first, then Bob (once you have stepped over a few more times).
- Single step some more until you reach Line 27.
- Observe that the variable i has appeared in the Variables window (top-right).
- As you single step some more you will see that p will appear, then disappear, as the loop is progressing. That's the life span of local variables in blocks! Make sure to open-up the p by clicking the triangle next to it, in the Variables window, and see what pair points to.
Finish Running the Program
- When you are satisfied that you have understood what you were single-stepping over, you can make the program resume going full speed. For this, just click the orange rectangle + green triangle icon (labeled Resume (F8)) on the top bar. This will run the program full speed until its normal end.
- If you do not want to resume the program, then kill it, using the red square. A good rule of thumb is that if a red square is showing on the Eclipse window, something is running or temporarily stopped. If you do not need it, then stop it by clicking on the red square!
That's it; you have the basics for debugging program. Remember to always set a breakpoint first. Then run/debug the program; this will make it go full-speed until the break point.
Part 2: Conditional Breakpoints
- Assume that you have a program that does a lot of computation in a loop before things start getting "strange," and you don't want to have to single-step through 100 iterations of a loop before you start reaching the place of interest in the computation.
- In this part we see how to set a breakpoint that becomes active only when some condition is met.
- Here's the program we're going to play with:
// DebugDemo2.java // D. Thiebaut public class DebugDemo2 { public static void main(String[] args) { long Fibn, Fibn_1 = 1, Fibn_2 = 1; long[] fib = new long[200]; fib[0] = fib[1] = 1; for ( int i=2; i < fib.length; i++ ) { Fibn = Fibn_1 + Fibn_2; fib[i] = Fibn; Fibn_2 = Fibn_1; Fibn_1 = Fibn; } } }
- We've seen this program before. It computes Fibonacci terms in a loop and stores them in an array. The problem with this code is that Fibonacci terms get large very fast, and at some point they overflow the long integer they are stored in.
- Just to make sure you understand the problem, just add a System.out.println( Fibn ) statement at the bottom of your loop, and verify that, indeed, Fibn becomes negative at some point.
- Did you see the negative numbers? Good; now remove the print statement!
- This program is simple enough that using print statements is enough to figure out where the bug is. In more complicated programs, though, might generate too much information. What if the problem manifests itself after a loop has iterated a million times?
Setting a Conditional Breakpoint
- Let's make the program stop when it reaches Line 11, and Fibn is negative:
- Right/Control click on Line 11 and set a breakpoint, as you did in Part 1.
- Right/Control click on Line 11 again, and this time pick Breakpoint Properties
- Click Conditional, Suspend thread, Suspend when true, and enter the following expression in the window:
Fibn < 0
- indicating that we want the breakpoint to activate, i.e. the program to stop, when (Fibn < 0) becomes true.
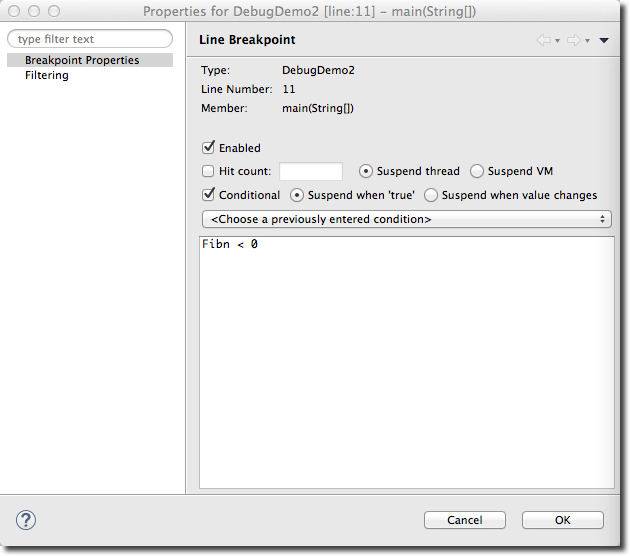
- Click Ok to close the window.
- Click on the bug icon to run your program.
- If everything goes well, it will stop on Line 11 when Fibn becomes negative.
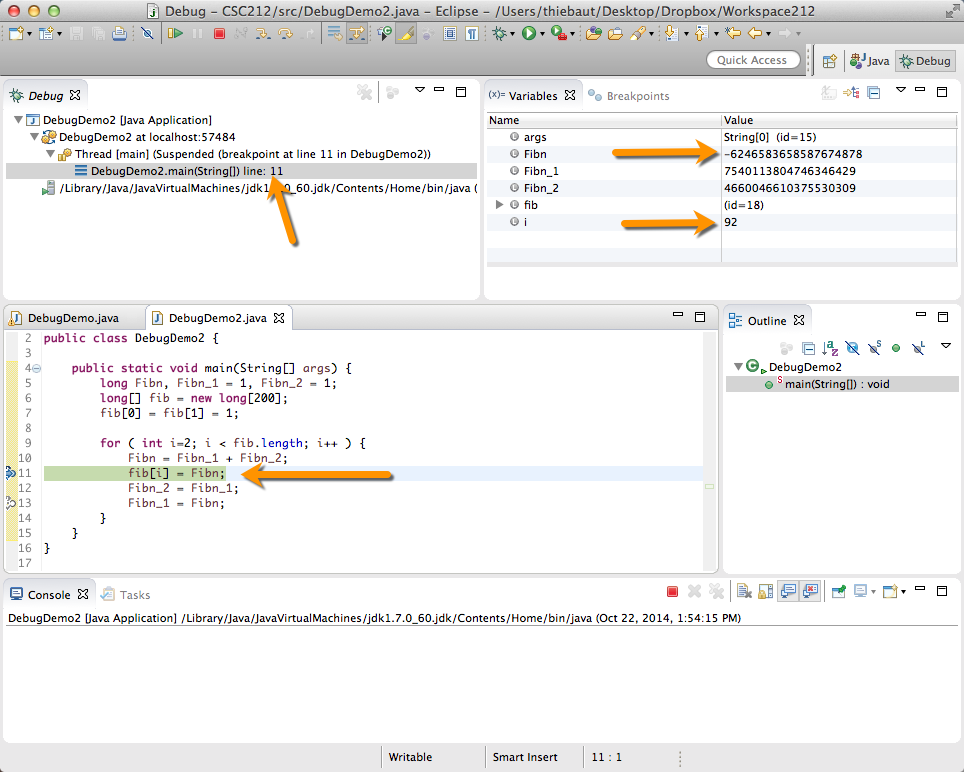
- Observe that the state of the program when the problem occurs is fully visible:
- Fibn is indeed negative (-6246583658587674878)
- i is 92, indicating that it occurs at Iteration 92 of the loop.
- we are indeed stopped on Line 11 of main(), in DebugDemo2.
- Click on the red square to kill the program.
Exercise
- Study the code below. Pay attention to the for-loop and what it computes.
import java.util.ArrayList; import java.util.UUID; class Triplet { public String s; int i, j; Triplet( String ss, int ii, int jj ) { s=ss; i=ii; j=jj; } public String toString() { return s+"("+i+ ", " + j + ")"; } } public class DebugDemo3 { static int seed = 1111; public static void main(String[] args) { ArrayList<Triplet> A = new ArrayList<Triplet>(); int x, y; for ( int i=0; i<10000; i++ ) { String randomString = UUID.randomUUID().toString(); x = randomInt(); y = randomInt(); A.add( new Triplet( randomString, x, y ) ); } } private static int randomInt() { int x = (11 + seed * 99563) % 104729; seed = (11 + x * 99563) % 104729; return seed & x; } }
- Without printing anything on the screen, figure out at what index i, the loop above generates a new triplet that has 68616 for x, and -131030 for y.