CSC270 Homework 1 2012
--D. Thiebaut 13:55, 1 February 2012 (EST)
Contents
This assignment is due Wednesday 2/8/12 at 1:10 p.m. No late assignment will be accepted. You can skip one assignment without penalty during the semester. This assignment must be done individually, and cannot be done in a group. Other assignments will give you a chance to work in pairs.
Problem #1
- Write the most concise expression (as an equation using + . and the bar over a symbol) of the boolean function f( a, b, c ) = Σ(0, 1, 2, 3, 7 ).
- Same question for g( a, b, c ) = Σ(0, 1, 2 )
- Same question for h( a, b, c ) = Σ(0, 1, 2, 3, 4, 5, 6, 7 )
- Same question for k( a, b, c ) = Σ(0, 1, 2, 3, 4, 6, 7 )
- A convention used to write not a in a boolean expression when writing it in an electronic document is to use the quote (prime) after a. So if you need to write f = not (a + b ) . ( not a + not c ), write it as follows:
f = ( a + b )' . ( a' + c' )
Problem #2
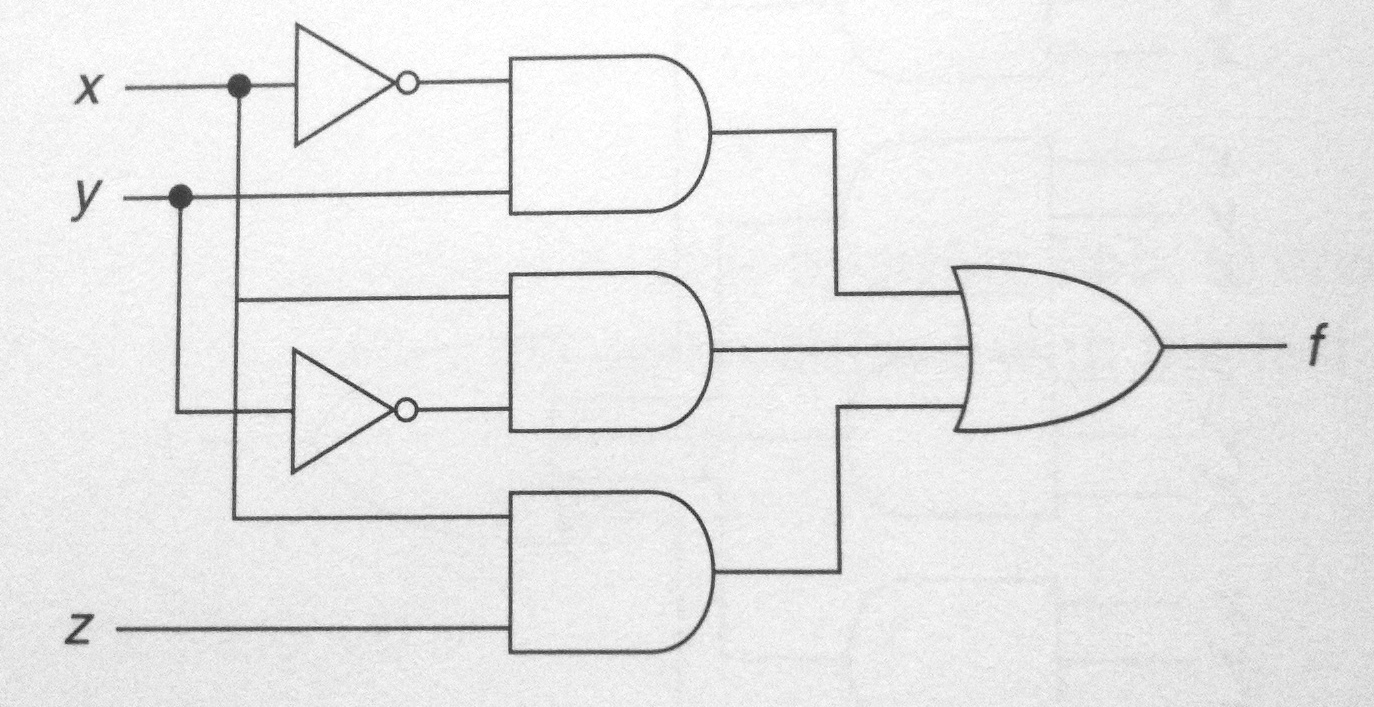
- What is the raw expression of the function f shown below? In other words, what is its direct translation of the diagram, without any simplification on your part? (Note the wire going from x to the second AND gate from the top should have a dot on it, to indicate that the signal is split from one wire to two.)
- What is the most concise expression of f? In other words, use the same simplification rules as in the previous question and see if you can simplify the expression of f. Verify that the two expressions you come up with (if any) give the same answer by writing a program (or adding new code to your previous program).
- What is the minterm form of f?
Note
- You may find this CSC103 lab of interest. It shows how to use a very simple circuit simulator to test logic designs.
Problem #3
- If f is equal to Σ(1, 2, 3 ) and g is equal to Σ(0, 4), what is the minterm canonical form of h, which is equal to f + g (+ is or)?
- Generalize to any function f and any function g for which you know the minterm canonical form, and which you or together to generate a new function.
- Same questions, but this time we and f and g together to get a new function k.