CSC212 Lab 12 2014
--D. Thiebaut (talk) 19:37, 9 November 2014 (EST)
Contents
This lab deals with Sorting algorithms, HeapSort, QuickSort, and methods used to avoid worst-case conditions.
Something Fun
Lab Problem #0: Observing Quicksort at Work
- Point your Firefox or Safari browser to this URL: http://cs.smith.edu/~dthiebaut/java/sort/Welcome.html. Chrome won't work with 64-bit Java Applets, so no need to try it...
- You may need to resize the window or shrink/expand the applet to see the Start Button.
Standard Quicksort, Random Array
- Select Standard Quicksort for the Sorting Algorithm
- Select Random for the Array Type
- Select Swap Square for the View
- Delay of 25
- Start!
- Notice how partition works. Whatever group of bars is red represent the partition that is being split into 2 around the pivot.
- Don't hesitate to run the experiment a few times until you "get it".
Standard Quicksort, Array in Increasing Order
- Click Stop so that you can start a new experiment.
- Select Standard Quicksort for the Sorting Algorithm
- Select Sorted Incr. Order for the Array Type
- Select Swap Square for the View
- Delay of 25
- Start!
- Notice how the partition is of size N first, then N-1, then N-2, etc.
Standard Quicksort, Array in Decreasing Order
- Click Stop so that you can start a new experiment.
- Select Standard Quicksort for the Sorting Algorithm
- Select Sorted Decr. Order for the Array Type
- Select Swap Square for the View
- Delay of 25
- Start!
- Notice how the partition is of size N first, then N-2, then N-4, etc.
Quicksort with a Random Pivot
- Repeat the same experiments above, (random array, sorted in increasing order, sorted in decreasing order), but pick "Quicksort with Random Pivot" as the algorithm.
- Does the random pivot help with the random array?
Quicksort with Median of Three Pivot
- Repeat the same experiments above, (random array, sorted in increasing order, sorted in decreasing order), but pick "Quicksort with Median of Three Pivot" as the algorithm. To refresh your memory, with the median of three, partition takes the median of the first, middle, and last number in the slice of the array it has to work on, as the pivot.
- Is this method more efficient than the random pivot for sorted arrays?
Quicksort with Tail Recursion Truncated
- Same experiments again, but this time pick the "Quicksort with Tail Recursion Truncated" algorithm. Try to answer the following questions to yourself, as a way of understanding how tail recursion works for Quicksort. Nothing to submit anywhere...
- Question 1
- Can you see the tail recursion being truncated? Which sorting method is used to sort the small partitions?
- Question 2
- Is the O(N^2) sorting routine called on all the small partitions, separately, or is it called on the whole array?
- Question 3
- Can you explain the two areas identified below?
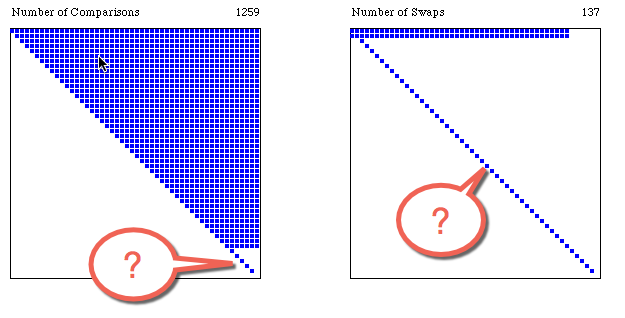
- Question 4
- Is the Quicksort algorithm cutting the tail recursion, also using a random pivot or not?
Lab Problem #1: Recursion-Stack Depth
- Create a class containing the code for Quicksort.
- Study the main function carefully before running the program. Make sure you understand how it operates.
- If you are using Eclipse, remember that command-line arguments are set in the "Run Configurations" panel, as explained in Homework 5, Problem 1.
- Run it on sorted arrays of size 10, 200, 500, 1000, 5000, 10000, 50000, 100000. Keep on increasing the size until something happens...
- You probably ran into an exception... Make sure you read what the exception is... Can you figure it out?
- Read the documentation of the -XSS command line on this page.
- Apply it to your program
- If you are using Eclipse, click on the Run top menu-option, then Run Configurations, then on the Arguments tab, and in the VM arguments window, enter something like -Xss4m (you'll have to do go through some trials and errors to find the right value.
- If you are running your Java code on beowulf, simply add the option on the command line for the Java Virtual Machine (in this case, a request for 64 Megabytes of stack size):
java -Xss64m QuickSort 1000000 random
- Make sure you have define a large enough stack to sort at least a million ints.
Lab Problem #2: HeapSort
- Java provides heap data structures, but calls them PriorityQueues.
- Instead of keeping the largest element at the top of the heap, PriorityQueues keep the smallest element at the top.
- Try the example below to see how to use a PriorityQueue
import java.util.PriorityQueue; public static void TestPrioQueues() { PriorityQueue<Integer> heap = new PriorityQueue<Integer>(); heap.add( 1 ); heap.add( 20 ); heap.add( 5 ); heap.add( 100 ); while ( ! heap.isEmpty() ) System.out.println( heap.poll() ); }
- Question 1
- Using some of the code/functions from this page, create a function called heapsort( int[] A ) that will use a priority queue to sort the array of ints A.
- Question 2
- Using the code snippet below, measure the execution times of QuickSort and of your HeapSort function. Figure out which is regularly faster on arrays of varying sizes.
long start = System.nanoTime(); quicksort(A, 0, A.length - 1); long end = System.nanoTime(); System.out.println( String.format( "quickSort( %d ) takes %1.3f msec", N, (end-start)/1000000.0f ) );
Lab Problem #3: Speeding Up QuickSort
- You will be modifying the QuickSort program of Problem #2. You should have modified it so that you can measure its execution time.
- Rename your file Lab12_3.java, and rename your class Lab12_3 (you will need to submit under that name to Moodle).
- Run it on sorted arrays of varying sizes (by providing different command line arguments) until you find an array size that requires between 1 and 10 seconds of execution time.
- Pick one of the methods you have observed in Section 0 of this lab, that makes Quicksort avoid worst case conditions, and implement it. Modify the code of Lab12_3.java.
- Verify that you have seriously improved your Quicksort function with this mod.
Moodle Submission
- Submit your program to Moodle. Your program will be run against the solution program on a sorted array. The grade is proportional to how close your execution time comes to the execution time of the solution program.
- Note: your program will be given the size of the array to sort, and whether the array is random, sorted in increasing order, or sorted in decreasing order, on the command line. Make sure your program gets N and the array type from the args array in main().

