revised --D. Thiebaut (talk) 14:53, 21 April 2017 (EDT)

This page is an introduction to the concept of Fixed-Point and Floating-Point numbers for assembly-language programmers of the Intel Pentium.

Introduction

In this course on assembly language we have actually spent all our time concentrating on integers. Unsigned, signed, 2's complement, all integer arithmetic. We know how to deal with series of integers, multiply integers, divide integers, and get the remainder and the quotient of the division, but we never dealt with real numbers, numbers such as 1.5, -0.0005, or 3.14159. The reason is that real numbers have a totally different format, and they need an altogether different processor architecture to perform arithmetic operations with them.

Before we look at the format, let's figure out if we can carry over the binary system to real numbers.

Review of the decimal system

Let's review how real numbers work in the decimal system. Let's take 123.45 for example:

      123.45 = 1x10² + 2x10¹ + 3x10⁰ + 4x10^-1 + 5x10^-2

Notice that the powers of 10 keep on diminishing by 1 when we pass the decimal point. Very logically. The first digit on the right side of the decimal point has weight 0.1. The second one 0.01, and so on.

Application to the Binary System: Unsigned Numbers

So, for unsigned binary numbers, we can use a similar system, and use negative powers of 2 for the digits that are on the right-hand side of the... ah, I was about to say "decimal point"... since we are dealing with a point between binary digits, we'll refer to it as binary point. (I will use binary point and decimal point interchangeably in the remainder of this page.)

      1101.11 = 1x2³ + 1x2² + 0x2¹ + 1x2⁰ + 1x2^-1 + 1x2^-2

If we compute the total value of this binary in decimal we get 8 + 4 + 1 + 0.5 + 0.25 = 13.75.

So, our conclusion is that if we know the location of the binary point, then we can easily represent fractional numbers in binary.

The most logical format to adopt then is to fix the location of the binary point, and assume that the bits that are higher than this location have weights that are 2^k where k is positive. All the digits lower than this location will have weight of the form 2ⁿ where n is negative.

One example would be to use 16-bit words and decide that the binary point lies between the upper and lower bytes. As illustrated below:

                    b₇b₆b₅b₄b₃b₂b₁b₀.b_-1b_-2b_-3b_-4b_-5b_-6b_-7b_-8

Notice the binary point, between the two groups of 8 bits.

We refer to a format where the decimal point is fixed between two groups of bits, as a fixed-point notation.

Note: we never store the decimal point in fixed point formatted numbers. The decimal point location is known and fixed, so we do not need to store the point. This is referred to as an implied binary point.

Definition

A number format where the numbers are unsigned and where we have a integer bits (on the left of the decimal point) and b fractional bits (on the right of the decimal point) is referred to as a U(a,b) fixed-point format^[1].

For example, if we have a 16-bit format where the implied binary point is between the two bytes is a U(8,8) format.

The actual value of an N-bit number in U(a,b) is

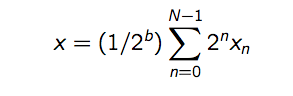
where x_n represents the bit at position n, x₀ representing the Least Significant bit.

Examples of unsigned numbers in Fixed-Point Notation

Let's pick a number in U(a, b) = U(4, 4) format to start with. Say x = 1011 1111 = 0xBF = 191d (decimal). What decimal number does x represent as a U(4, 4) number?

x = 1011.1111 = 8 + 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 11.9375

Another way to get this same result is to also say that x is the value of the unsigned integer 0xBF divided by 2^b. Since in our case b is 4, this yields:

x = 191 / 2⁴ = 191 / 16 = 11.9375

Here are some more examples of unsigned numbers, but this time in U(8, 8) format:

0000000100000000 = 0000001 . 00000000 = 1d (1 decimal)

0000001000000000 = 0000010 . 00000000 = 2d

0000001010000000 = 00000010 . 10000000 = 2.5d

Exercises with the Unsigned Fixed-Point Format

It might be useful to have a table of the first 20 negative powers of 2:

2^-0 = 1	2^-1 = 0.5	2^-2 = 0.25
2^-3 = 0.125	2^-4 = 0.0625	2^-5 = 0.03125
2^-6 = 0.015625	2^-7 = 0.0078125	2^-8 = 0.00390625
2^-9 = 0.00195312	2^-10 = 0.000976562	2^-11 = 0.000488281
2^-12 = 0.000244141	2^-13 = 0.00012207	2^-14 = 6.10352e-05
2^-15 = 3.05176e-05	2^-16 = 1.52588e-05	2^-17 = 7.62939e-06
2^-18 = 3.8147e-06	2^-19 = 1.90735e-06	2^-20 = 9.53674e-07

Assume a 16-bit fixed-point U( 8, 8 ) format. Answer the following questions.

What is the decimal equivalent of these two binary numbers followed by a hex number?

0000 0000 1000 0000

1000 0000 1000 0000

0x4040

What is the binary representation of the following two decimal numbers in U(8, 8)? In U(4, 4)?

12.25

16.125

What is the smallest number we can represent with the U(8, 8) format?

What is the largest number we can represent with the U(8, 8) format?

Fixed-Point Format for Signed Numbers

Fortunately, the fixed-point format we have just developed also works for 2's complement numbers. For an N-bit unsigned integer number, the weight of the most significant bit (MSB) is 2^N-1. The weight of the MSB for a 2's complement number is simply -2^N-1.

When dealing with N-bit signed numbers, we adopt a different notation and refer to the format where we have a sign bit, a integer bits and b fractional bits as an A(a, b) format. Note that this is slightly different from the U(a, b) notation where we have N = a + b. With the A(a, b), N= 1+a+b.

In an N-bit format A( a, b ), the value of a binary number becomes:

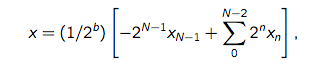
Examples of Signed Fixed-Point Numbers

Some unsigned numbers in A(7,8) format. N = 1 + 7 + 8 = 16.

00000000100000000 = 00000001 . 00000000 = 1d

10000000100000000 = 10000001 . 00000000 = -128 + 1 = -127d

0000001000000000 = 0000010 . 00000000 = 2d (2 decimal)

1000001000000000 = 1000010 . 00000000 = -128 + 2 = -126d

0000001010000000 = 00000010 . 10000000 = 2.5d

1000001010000000 = 10000010 . 10000000 = -128 + 2.5 = -125.5d

Exercises with the Signed Fixed-Point Format

What is -1 in A(7,8)?
What is -1 in A(3,4)?
What is 0 in A(7,8)?
What is the smallest number one can represent in A(7,8)?
The largest in A(7,8)?

Properties and Rules for Arithmetic

Unsigned Range: The range of U(a, b) is 0 ≤ x ≤ 2^a − 2^−b.
Signed Range: The range of A(a, b) is −2^a ≤ x ≤ 2^a − 2^−b.
Two numbers in different format must be scaled before being added together. In other words the binary points must be aligned before the addition can be performed
The sum of two numbers in A(a, b) format is in A(a+1,b) format. Similarly for numbers in U(a, b) format, their sum becomes U(a+1, b ).
The multiplication of two numbers in U(a, b) and U(c, d) formats results in a product in U( a+c, b+d) format.
The multiplication of two numbers in A(a, b) and A(c, d) formats results in a product in A( a+c+1, b+d) format.

Definitions

The definitions below are taken from Randy Yate's excellent paper^[1] on the Fixed-Point notation.

Precision

Precision is not always defined the same way. According to ^[1], it is the maximum number of non-zero bits representable. For example, an A(13,2) number has a precision of 16 bits. For ﬁxed-point representations, precision is equal to the wordlength.

However, according to ^[2], the entry on Fixed-Point in Wikibooks</ref>, the precision of a fixed-point format is the number of fractional bits, or b, in A(a, b), or U(a, b ).

Range

Range is the diﬀerence between the most negative number representable and the most positive number representable.

For example, an A(13,2) number has a range from -8192 to +8191.75, i.e., 16383.75.

The range for a U(8, 8) would be 2^-8 to 2^8 - 2^-8, which we can represent a follows:

  ---+-----------+-----------+-----------+-----------+----------   ----------+--------------------
     0         2^-8        2.2^-8      3.2^-8      4.2^-8       ...       2^8-2^-8
                 |    	      	      	      	      	      	      	    |
           smallest number representable   	      	      	       largest one

Resolution

The resolution is the smallest non-zero magnitude representable. For example, an A(13,2) has a resolution of 1/2² = 0.25. This is also the size of the regular intervals between the values representable with the format, as illustrated below for a U(8, 8) format.

  ---+-----------+-----------+-----------+-----------+----------   ----------+--------------------
     0         2^-8        2.2^-8      3.2^-8      4.2^-8       ...       2^8-2^-8
     |<--------->|           |<--------->|
      resolution      	     	resolution

Accuracy

Accuracy is the magnitude of the maximum diﬀerence between a real value and it’s representation. For example, the accuracy of an A(13,2) number is 1/8. Note that accuracy and resolution are related as follows:

Accuracy(F) = Resolution(F)/2

where F is a number format.

The accuracy of a U(8, 8) format is illustrated below:

  ---+-----------+-----------+-----|-----+-----------+----------   ----------+--------------------
     0         2^-8        2.2^-8  |   3.2^-8      4.2^-8       ...       2^8-2^-8
      	      	      	      	   |
      	      	      	      	   | real value we need to represent
      	      	      	     <--->
      	      	      	    Accuracy is	the largest such difference

Exercises on Accuracy and Resolution

What is the accuracy of an U(7,8) number format? What is its resolution? What is the smallest number one can represent in such a format? What is the largest number?

Comment on how a U(7,8) format is "fair" in its representation of small numbers, and of large numbers.

Floating-Point Numbers

The CS department at Berkeley has an interesting page on the history of the IEEE Floating point format^[3]. You will enjoy reading about the strange world programmers were confronted with in the 60s.

Here are examples of floating-point numbers in base 10:

        6.02 x 10²³

        -0.000001

        1.23456789 x 10^-19

        -1.0

A floating-point number is a number where the decimal point can float. This is best illustrated by taking one of the numbers above and showing it in different ways:

        1.23456789 x 10^-19 = 12.3456789 x 10^-20

                          = 0.000 000 000 000 000 000 123 456 789 x 10⁰

Notice that the decimal point is moving around, floating around, thanks to the exponent of 10.

Notice as well, that the floating point numbers can be positive or negative, as well, and that the exponent of 10 can be positive or negative.

The IEEE Format for 32-bit Floating-Point Numbers

Wikipedia has a very good page on the Floating Point notation^[4], as well as on the IEEE Format^[5]. They are good reference material for this subect.

We will concentrate here on the IEEE Format, which now is a standard used by most processors for their floating point units, and by most compilers.

By the way, when you use floats or doubles in Java, you use IEEE Floating Point numbers.

The Format

First, the base. The IEEE Floating Point format uses binary to represent real numbers. While this seems like an obvious choice, the IEEE could have used another base for the exponent. More on that later...

There are several different word length for the IEEE, including 32 bits, 64 bits, and 80 bits. We'll concentrate on the 32-bit format. In this format, every real number x is written the same way:

                      x  =  +/- 1.bbbbbb....bbb  x 2^bbb...bb

where the bs represent individual bits.

Observations and Definitions

+/- is the sign. It is represented by a bit, equal to 0 if the number is positive, 1 if negative.
the part 1.bbbbbb....bbb is called the mantissa
the part bbb...bb is called the exponent
2 is the base for the exponent.
the number is normalized so that its binary point is moved to the right of the leading 1. Because the binary point is floating, it is possible to bring it to the right of the most significant 1 (except in some special cases which we'll cover soon).
the binary point divides the mantissa into the leading 1 and the rest of the mantissa.
because the leading bit will always be 1 (again, there might be some exceptions), we don't need to store it. This bit will be an implied bit.

Packing and Coding the Bits

First, when we have a real number we need to normalize it by 1) bringing the binary point to the right of the leading 1 and 2) by adjusting the exponent at the same time.

For example, assume we have the following real number expressed in binary:

           y =  +1000.100111

We can normalize it as follows:

           y = +1.000100111 x 2³

Where we have expressed the mantissa in binary, and the exponent part in decimal to better highlight the fact that moving the binary point 3 places to the left is the same as dividing the mantissa by 8, and hence the exponent multiplies the mantissa back by 2³, or 8.

If we want to represent y completely in binary, we get:

           y = +1.000100111 x 10¹¹

since 2 decimal is 10 in binary, and 3 is 11. Right?

So, to store y in a double word, we only need to store 3 pieces of information:

0 to represent +,
000100111 for the mantissa (remember that the leading 1 is implied, and thus we don't store it), and
we need to store 11 for the exponent.

When storing y in a 32-bit double-word, the following placement of bits is adopted:

   31 30      23 22   	      	       0
 +---+----------+-----------------------+
 | s | exponent |       mantissa        | 
 | 1 | 8        |          23           |
 +---+----------+-----------------------+

the MSB is the sign bit of the mantissa: 0 for positive, 1 for negative
the exponent is stored in the next 8 bits. The stored value for the exponent ranges from 0 to 255.
the mantissa without the leading 1. part is stored in the lower 23 bits. It's magic, we can actually store the most significant 24 bits of the real mantissa in 23 bits. Nice trick!

So y in a 32-bit double word looks like this:

 y = 0 bbbbbbbb 0001001110000000000000

You will noticed that I haven't shown the exponent in binary. This is because the IEEE committee that drafted the standard for floating point numbers decided not to use the 2's complement to code the exponent. Instead it uses what is called a bias. The reason for this will become clear later. The table below illustrates the coding of the exponent.

real exponent	stored exponent	Comments
-126	0	Special Case #1
-126 -125 -124 -123 . . . -1	1 2 3 4 . . . 126
0	127
1 2 3 . . . 127	128 129 130 . . . 254
128	255	Special Case #2

So, since our real exponent is 3, we add 127 to it and get 130, which in binary is 1000 0010, and that is the value that is actually stored in the floating point number.

We now have the complete IEEE representation of y: y = 0 10000010 0001001110000000000000.

Exercises with Floating-Point Numbers

How is 1.0 coded as a 32-bit floating point number?
What about 0.5?
1.5?
-1.5?
what floating-point value is stored in the 32-bit number below?

1 | 1000 0010 | 111 1000 0000 0000 0000 0000

Special Cases

There are several special cases, or exceptions to the rule we have just presented for constructing floating-point numbers:

zero
very small numbers
very large numbers

Zero

The value 0 expressed in binary does not have a single 1 in it. So how could we normalize 0 and put the binary point on the right of the leading 1? Answer: we can't. So with the IEEE format, 0 is represented by 32 bits set to 0. In other words, a mantissa of 0, an exponent of 0, and a sign of 0 represent the value zero.

      0.0  = 0 00000000 0000000000000000000000

Very Small Numbers

When the stored exponent of a floating point number is 0, it means that the real exponent is -126, so the mantissa is multiplied by 2^-126, which is a very small quantity. In this case the format stipulates that the mantissa does not have an implied leading bit of 1. This means that if the stored exponent is 0, and if the mantissa is different from 0, and happens to be, say, 0001000...0, then the mantissa actually is 0.0001000...0, without a leading 1 on the left of the binary point. This allows the format to represent smaller real numbers that couldn't have been representable otherwise.

Example

what real value is represented by 0 | 00000000 | 00100000000000000000000 in the IEEE Floating Point format?

exponent = 0 ==> denormal number, true exponent = -126
mantissa of denormal numbers have no hidden 1: mantissa = 0.001, which in decimal is 0.125.
the value of this number is 0.125 * 2^-126 = 1.4693679e-39

Very Large Numbers

Infinities

At the other end of the spectrum, when the stored exponent is 255, representing a true exponent of 127, then the mantissa is multiplied by the largest possible power of 2: 2¹²⁷. In this case, if the mantissa is all 0, the value represented is infinity. Yes, infinity! The IEEE format provide this value so that when some operations are performed with floating-point numbers that result in values whose magnitude is larger than what can be stored in the 32-bit word, then the special value of infinity or ∞ is forced in the 32-bit word. Because the sign bit can be either 0 or 1, we can represent +∞ and -∞.

     +∞ = 0 11111111 00000000000000000000000

     -∞ = 1 11111111 00000000000000000000000

NaN

But what if we have the largest possible stored exponent (255) and a mantissa that is not all 0? The answer is that this special value is called NaN, which stands for Not a Number^[6]. NaN is a perfectly valid value for a real number, but very few programmers actually know about it, or have ran into it. It usually results when some operation results in an impossible value to compute.

Wikipedia^[6] lists the operations that can create NaNs. Some of the most common ones include division by 0, 0⁰, 1^∞, and square root of a negative number, among others.

An interesting aspect of the NaN value is that it is sticking, that is when you combine NaN with any other number through an arithmetic operation, or through a mathematical function, the result will always be NaN, which is a safe way to detect when incorrect results are computed.

Below is a program that generates NaNs, taken from StackOverflow.com^[7]:

import java.util.*;
import static java.lang.Double.NaN;
import static java.lang.Double.POSITIVE_INFINITY;
import static java.lang.Double.NEGATIVE_INFINITY;

public class GenerateNaN {
	public static void main(String args[]) {
		double[] allNaNs = { 0D / 0D, POSITIVE_INFINITY / POSITIVE_INFINITY,
				POSITIVE_INFINITY / NEGATIVE_INFINITY,
				NEGATIVE_INFINITY / POSITIVE_INFINITY,
				NEGATIVE_INFINITY / NEGATIVE_INFINITY, 0 * POSITIVE_INFINITY,
				0 * NEGATIVE_INFINITY, Math.pow(1, POSITIVE_INFINITY),
				POSITIVE_INFINITY + NEGATIVE_INFINITY,
				NEGATIVE_INFINITY + POSITIVE_INFINITY,
				POSITIVE_INFINITY - POSITIVE_INFINITY,
				NEGATIVE_INFINITY - NEGATIVE_INFINITY, Math.sqrt(-1),
				Math.log(-1), Math.asin(-2), Math.acos(+2), };
		System.out.println(Arrays.toString(allNaNs));
		// prints "[NaN, NaN...]"
		System.out.println(NaN == NaN); // prints "false"
		System.out.println(Double.isNaN(NaN)); // prints "true"
	}
}

Its output is shown below:

[NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN]
false
true

Range of Floating-Point Numbers

The range, i.e. the amount of "space" covered on the real line, from -infinity to +infinity is given in the next table, where we show the normalized and denormalized ranges for single (32 bits) and double (64 bits) precisions.

	Denormalized	Normalized	Approximate Decimal
Single Precision	± 2^-149 to (1-2^-23)×2^-126	± 2^-126 to (2-2^-23)×2¹²⁷	± ~10^-44.85 to ~10^38.53
Double Precision	± 2^-1074 to (1-2^-52)×2^-1022	± 2^-1022 to (2-2^-52)×2¹⁰²³	± ~10^-323.3 to ~10^308.3

But if you want to remember the effective range that is afforded by the two precisions, remember this simplified table:

	Binary	Decimal
Single Precision	± (2-2^-23) × 2¹²⁷	~ ± 10^38.53
Double Precision	± (2-2^-52) × 2¹⁰²³	~ ± 10^308.25

The gap between floats is not constant, as with Fixed-Point

Because floating-point numbers have an exponent, the larger the number is, the farther away it is from its direct neighbors. This is best illustrated if we consider the format with only 8 bits in length, with 1 bit for the sign, 3 bits for the exponent, and 4 bits for the mantissa. 3 bits for the exponent means that the largest stored exponent will be 7, and hence our bias will be 3.

The table below shows all the real numbers we could represent with such a format ( here's the program used to generate the table).

Notice that when the numbers are large, the difference between two consecutive floats is large. For example -15.5 and -15.0. The format cannot represent any real number in between. But when the numbers are small in magnitude, the difference between two of them can be quite small, as with 0.015625 and 0.0078125.

real value	byte integer	stored [sign exp mantissa]	floating point
-inf	240	1 111 0000	-inf
-15.5	239	1 110 1111	- 1.9375 * 2^ 3
-15.0	238	1 110 1110	- 1.875 * 2^ 3
-14.5	237	1 110 1101	- 1.8125 * 2^ 3
-14.0	236	1 110 1100	- 1.75 * 2^ 3
-13.5	235	1 110 1011	- 1.6875 * 2^ 3
-13.0	234	1 110 1010	- 1.625 * 2^ 3
-12.5	233	1 110 1001	- 1.5625 * 2^ 3
-12.0	232	1 110 1000	- 1.5 * 2^ 3
-11.5	231	1 110 0111	- 1.4375 * 2^ 3
-11.0	230	1 110 0110	- 1.375 * 2^ 3
-10.5	229	1 110 0101	- 1.3125 * 2^ 3
-10.0	228	1 110 0100	- 1.25 * 2^ 3
-9.5	227	1 110 0011	- 1.1875 * 2^ 3
-9.0	226	1 110 0010	- 1.125 * 2^ 3
-8.5	225	1 110 0001	- 1.0625 * 2^ 3
-8.0	224	1 110 0000	- 1.0 * 2^ 3
-7.75	223	1 101 1111	- 1.9375 * 2^ 2
-7.5	222	1 101 1110	- 1.875 * 2^ 2
-7.25	221	1 101 1101	- 1.8125 * 2^ 2
-7.0	220	1 101 1100	- 1.75 * 2^ 2
-6.75	219	1 101 1011	- 1.6875 * 2^ 2
-6.5	218	1 101 1010	- 1.625 * 2^ 2
-6.25	217	1 101 1001	- 1.5625 * 2^ 2
-6.0	216	1 101 1000	- 1.5 * 2^ 2
-5.75	215	1 101 0111	- 1.4375 * 2^ 2
-5.5	214	1 101 0110	- 1.375 * 2^ 2
-5.25	213	1 101 0101	- 1.3125 * 2^ 2
-5.0	212	1 101 0100	- 1.25 * 2^ 2
-4.75	211	1 101 0011	- 1.1875 * 2^ 2
-4.5	210	1 101 0010	- 1.125 * 2^ 2
-4.25	209	1 101 0001	- 1.0625 * 2^ 2
-4.0	208	1 101 0000	- 1.0 * 2^ 2
-3.875	207	1 100 1111	- 1.9375 * 2^ 1
-3.75	206	1 100 1110	- 1.875 * 2^ 1
-3.625	205	1 100 1101	- 1.8125 * 2^ 1
-3.5	204	1 100 1100	- 1.75 * 2^ 1
-3.375	203	1 100 1011	- 1.6875 * 2^ 1
-3.25	202	1 100 1010	- 1.625 * 2^ 1
-3.125	201	1 100 1001	- 1.5625 * 2^ 1
-3.0	200	1 100 1000	- 1.5 * 2^ 1
-2.875	199	1 100 0111	- 1.4375 * 2^ 1
-2.75	198	1 100 0110	- 1.375 * 2^ 1
-2.625	197	1 100 0101	- 1.3125 * 2^ 1
-2.5	196	1 100 0100	- 1.25 * 2^ 1
-2.375	195	1 100 0011	- 1.1875 * 2^ 1
-2.25	194	1 100 0010	- 1.125 * 2^ 1
-2.125	193	1 100 0001	- 1.0625 * 2^ 1
-2.0	192	1 100 0000	- 1.0 * 2^ 1
-1.9375	191	1 011 1111	- 1.9375 * 2^ 0
-1.875	190	1 011 1110	- 1.875 * 2^ 0
-1.8125	189	1 011 1101	- 1.8125 * 2^ 0
-1.75	188	1 011 1100	- 1.75 * 2^ 0
-1.6875	187	1 011 1011	- 1.6875 * 2^ 0
-1.625	186	1 011 1010	- 1.625 * 2^ 0
-1.5625	185	1 011 1001	- 1.5625 * 2^ 0
-1.5	184	1 011 1000	- 1.5 * 2^ 0
-1.4375	183	1 011 0111	- 1.4375 * 2^ 0
-1.375	182	1 011 0110	- 1.375 * 2^ 0
-1.3125	181	1 011 0101	- 1.3125 * 2^ 0
-1.25	180	1 011 0100	- 1.25 * 2^ 0
-1.1875	179	1 011 0011	- 1.1875 * 2^ 0
-1.125	178	1 011 0010	- 1.125 * 2^ 0
-1.0625	177	1 011 0001	- 1.0625 * 2^ 0
-1.0	176	1 011 0000	- 1.0 * 2^ 0
-0.96875	175	1 010 1111	- 1.9375 * 2^ -1
-0.9375	174	1 010 1110	- 1.875 * 2^ -1
-0.90625	173	1 010 1101	- 1.8125 * 2^ -1
-0.875	172	1 010 1100	- 1.75 * 2^ -1
-0.84375	171	1 010 1011	- 1.6875 * 2^ -1
-0.8125	170	1 010 1010	- 1.625 * 2^ -1
-0.78125	169	1 010 1001	- 1.5625 * 2^ -1
-0.75	168	1 010 1000	- 1.5 * 2^ -1
-0.71875	167	1 010 0111	- 1.4375 * 2^ -1
-0.6875	166	1 010 0110	- 1.375 * 2^ -1
-0.65625	165	1 010 0101	- 1.3125 * 2^ -1
-0.625	164	1 010 0100	- 1.25 * 2^ -1
-0.59375	163	1 010 0011	- 1.1875 * 2^ -1
-0.5625	162	1 010 0010	- 1.125 * 2^ -1
-0.53125	161	1 010 0001	- 1.0625 * 2^ -1
-0.5	160	1 010 0000	- 1.0 * 2^ -1
-0.484375	159	1 001 1111	- 1.9375 * 2^ -2
-0.46875	158	1 001 1110	- 1.875 * 2^ -2
-0.453125	157	1 001 1101	- 1.8125 * 2^ -2
-0.4375	156	1 001 1100	- 1.75 * 2^ -2
-0.421875	155	1 001 1011	- 1.6875 * 2^ -2
-0.40625	154	1 001 1010	- 1.625 * 2^ -2
-0.390625	153	1 001 1001	- 1.5625 * 2^ -2
-0.375	152	1 001 1000	- 1.5 * 2^ -2
-0.359375	151	1 001 0111	- 1.4375 * 2^ -2
-0.34375	150	1 001 0110	- 1.375 * 2^ -2
-0.328125	149	1 001 0101	- 1.3125 * 2^ -2
-0.3125	148	1 001 0100	- 1.25 * 2^ -2
-0.296875	147	1 001 0011	- 1.1875 * 2^ -2
-0.28125	146	1 001 0010	- 1.125 * 2^ -2
-0.265625	145	1 001 0001	- 1.0625 * 2^ -2
-0.25	144	1 001 0000	- 1.0 * 2^ -2
-0.1171875	143	1 000 1111	- 0.9375 * 2^ -3
-0.109375	142	1 000 1110	- 0.875 * 2^ -3
-0.1015625	141	1 000 1101	- 0.8125 * 2^ -3
-0.09375	140	1 000 1100	- 0.75 * 2^ -3
-0.0859375	139	1 000 1011	- 0.6875 * 2^ -3
-0.078125	138	1 000 1010	- 0.625 * 2^ -3
-0.0703125	137	1 000 1001	- 0.5625 * 2^ -3
-0.0625	136	1 000 1000	- 0.5 * 2^ -3
-0.0546875	135	1 000 0111	- 0.4375 * 2^ -3
-0.046875	134	1 000 0110	- 0.375 * 2^ -3
-0.0390625	133	1 000 0101	- 0.3125 * 2^ -3
-0.03125	132	1 000 0100	- 0.25 * 2^ -3
-0.0234375	131	1 000 0011	- 0.1875 * 2^ -3
-0.015625	130	1 000 0010	- 0.125 * 2^ -3
-0.0078125	129	1 000 0001	- 0.0625 * 2^ -3
0.0	0	0 000 0000	0
0.0078125	1	0 000 0001	+ 0.0625 * 2^ -3
0.015625	2	0 000 0010	+ 0.125 * 2^ -3
0.0234375	3	0 000 0011	+ 0.1875 * 2^ -3
0.03125	4	0 000 0100	+ 0.25 * 2^ -3
0.0390625	5	0 000 0101	+ 0.3125 * 2^ -3
0.046875	6	0 000 0110	+ 0.375 * 2^ -3
0.0546875	7	0 000 0111	+ 0.4375 * 2^ -3
0.0625	8	0 000 1000	+ 0.5 * 2^ -3
0.0703125	9	0 000 1001	+ 0.5625 * 2^ -3
0.078125	10	0 000 1010	+ 0.625 * 2^ -3
0.0859375	11	0 000 1011	+ 0.6875 * 2^ -3
0.09375	12	0 000 1100	+ 0.75 * 2^ -3
0.1015625	13	0 000 1101	+ 0.8125 * 2^ -3
0.109375	14	0 000 1110	+ 0.875 * 2^ -3
0.1171875	15	0 000 1111	+ 0.9375 * 2^ -3
0.25	16	0 001 0000	+ 1.0 * 2^ -2
0.265625	17	0 001 0001	+ 1.0625 * 2^ -2
0.28125	18	0 001 0010	+ 1.125 * 2^ -2
0.296875	19	0 001 0011	+ 1.1875 * 2^ -2
0.3125	20	0 001 0100	+ 1.25 * 2^ -2
0.328125	21	0 001 0101	+ 1.3125 * 2^ -2
0.34375	22	0 001 0110	+ 1.375 * 2^ -2
0.359375	23	0 001 0111	+ 1.4375 * 2^ -2
0.375	24	0 001 1000	+ 1.5 * 2^ -2
0.390625	25	0 001 1001	+ 1.5625 * 2^ -2
0.40625	26	0 001 1010	+ 1.625 * 2^ -2
0.421875	27	0 001 1011	+ 1.6875 * 2^ -2
0.4375	28	0 001 1100	+ 1.75 * 2^ -2
0.453125	29	0 001 1101	+ 1.8125 * 2^ -2
0.46875	30	0 001 1110	+ 1.875 * 2^ -2
0.484375	31	0 001 1111	+ 1.9375 * 2^ -2
0.5	32	0 010 0000	+ 1.0 * 2^ -1
0.53125	33	0 010 0001	+ 1.0625 * 2^ -1
0.5625	34	0 010 0010	+ 1.125 * 2^ -1
0.59375	35	0 010 0011	+ 1.1875 * 2^ -1
0.625	36	0 010 0100	+ 1.25 * 2^ -1
0.65625	37	0 010 0101	+ 1.3125 * 2^ -1
0.6875	38	0 010 0110	+ 1.375 * 2^ -1
0.71875	39	0 010 0111	+ 1.4375 * 2^ -1
0.75	40	0 010 1000	+ 1.5 * 2^ -1
0.78125	41	0 010 1001	+ 1.5625 * 2^ -1
0.8125	42	0 010 1010	+ 1.625 * 2^ -1
0.84375	43	0 010 1011	+ 1.6875 * 2^ -1
0.875	44	0 010 1100	+ 1.75 * 2^ -1
0.90625	45	0 010 1101	+ 1.8125 * 2^ -1
0.9375	46	0 010 1110	+ 1.875 * 2^ -1
0.96875	47	0 010 1111	+ 1.9375 * 2^ -1
1.0	48	0 011 0000	+ 1.0 * 2^ 0
1.0625	49	0 011 0001	+ 1.0625 * 2^ 0
1.125	50	0 011 0010	+ 1.125 * 2^ 0
1.1875	51	0 011 0011	+ 1.1875 * 2^ 0
1.25	52	0 011 0100	+ 1.25 * 2^ 0
1.3125	53	0 011 0101	+ 1.3125 * 2^ 0
1.375	54	0 011 0110	+ 1.375 * 2^ 0
1.4375	55	0 011 0111	+ 1.4375 * 2^ 0
1.5	56	0 011 1000	+ 1.5 * 2^ 0
1.5625	57	0 011 1001	+ 1.5625 * 2^ 0
1.625	58	0 011 1010	+ 1.625 * 2^ 0
1.6875	59	0 011 1011	+ 1.6875 * 2^ 0
1.75	60	0 011 1100	+ 1.75 * 2^ 0
1.8125	61	0 011 1101	+ 1.8125 * 2^ 0
1.875	62	0 011 1110	+ 1.875 * 2^ 0
1.9375	63	0 011 1111	+ 1.9375 * 2^ 0
2.0	64	0 100 0000	+ 1.0 * 2^ 1
2.125	65	0 100 0001	+ 1.0625 * 2^ 1
2.25	66	0 100 0010	+ 1.125 * 2^ 1
2.375	67	0 100 0011	+ 1.1875 * 2^ 1
2.5	68	0 100 0100	+ 1.25 * 2^ 1
2.625	69	0 100 0101	+ 1.3125 * 2^ 1
2.75	70	0 100 0110	+ 1.375 * 2^ 1
2.875	71	0 100 0111	+ 1.4375 * 2^ 1
3.0	72	0 100 1000	+ 1.5 * 2^ 1
3.125	73	0 100 1001	+ 1.5625 * 2^ 1
3.25	74	0 100 1010	+ 1.625 * 2^ 1
3.375	75	0 100 1011	+ 1.6875 * 2^ 1
3.5	76	0 100 1100	+ 1.75 * 2^ 1
3.625	77	0 100 1101	+ 1.8125 * 2^ 1
3.75	78	0 100 1110	+ 1.875 * 2^ 1
3.875	79	0 100 1111	+ 1.9375 * 2^ 1
4.0	80	0 101 0000	+ 1.0 * 2^ 2
4.25	81	0 101 0001	+ 1.0625 * 2^ 2
4.5	82	0 101 0010	+ 1.125 * 2^ 2
4.75	83	0 101 0011	+ 1.1875 * 2^ 2
5.0	84	0 101 0100	+ 1.25 * 2^ 2
5.25	85	0 101 0101	+ 1.3125 * 2^ 2
5.5	86	0 101 0110	+ 1.375 * 2^ 2
5.75	87	0 101 0111	+ 1.4375 * 2^ 2
6.0	88	0 101 1000	+ 1.5 * 2^ 2
6.25	89	0 101 1001	+ 1.5625 * 2^ 2
6.5	90	0 101 1010	+ 1.625 * 2^ 2
6.75	91	0 101 1011	+ 1.6875 * 2^ 2
7.0	92	0 101 1100	+ 1.75 * 2^ 2
7.25	93	0 101 1101	+ 1.8125 * 2^ 2
7.5	94	0 101 1110	+ 1.875 * 2^ 2
7.75	95	0 101 1111	+ 1.9375 * 2^ 2
8.0	96	0 110 0000	+ 1.0 * 2^ 3
8.5	97	0 110 0001	+ 1.0625 * 2^ 3
9.0	98	0 110 0010	+ 1.125 * 2^ 3
9.5	99	0 110 0011	+ 1.1875 * 2^ 3
10.0	100	0 110 0100	+ 1.25 * 2^ 3
10.5	101	0 110 0101	+ 1.3125 * 2^ 3
11.0	102	0 110 0110	+ 1.375 * 2^ 3
11.5	103	0 110 0111	+ 1.4375 * 2^ 3
12.0	104	0 110 1000	+ 1.5 * 2^ 3
12.5	105	0 110 1001	+ 1.5625 * 2^ 3
13.0	106	0 110 1010	+ 1.625 * 2^ 3
13.5	107	0 110 1011	+ 1.6875 * 2^ 3
14.0	108	0 110 1100	+ 1.75 * 2^ 3
14.5	109	0 110 1101	+ 1.8125 * 2^ 3
15.0	110	0 110 1110	+ 1.875 * 2^ 3
15.5	111	0 110 1111	+ 1.9375 * 2^ 3
inf	112	0 111 0000	+ inf

This range is illustrated below in a graph showing each represented real number between -15.5 and +15.5.

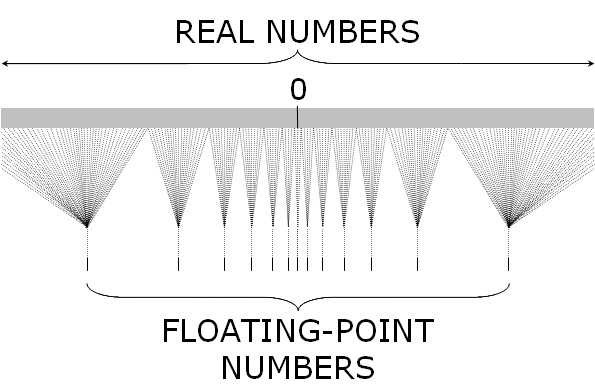
Another good representation of the varying resolution of the format is illustrated by this picture, taken from Izquierdo & Polhill article on floating-point errors^[8].

Why a bias of 127 instead of using 2's complement?

The reason the IEEE format uses a bias rather than 2's complement for the exponent is obvious when you look at several values and their representation in binary:

0.00000005	=	0 01100110 10101101011111110010101
1	=	0 01111111 00000000000000000000000
65536.5	=	0 10001111 00000000000000001000000

Notice that the 3 numbers are listed in increasing order of magnitude, and if you look at the exponents, they as well are in increasing order. It means that if you have two positive floating point numbers and you want to know which one is larger than the other one, you can do a simple comparison of the two as if they were unsigned integers, and you get the correct answer. And the best part is that you don't have to unpack the floating-point numbers in order to compare them. The same is true of two negative floating point numbers: if you clear the sign bits, the one with the largest unsigned magnitude is more negative than the other one. You can figure out how to compare one positive float to a negative float! :-)

Time to Play: An Applet

Click on the image below to open up Harald Schmidt's neat Floating-Point to Decimal converter. An alternative is this converter, created by Werner Randelshofer.

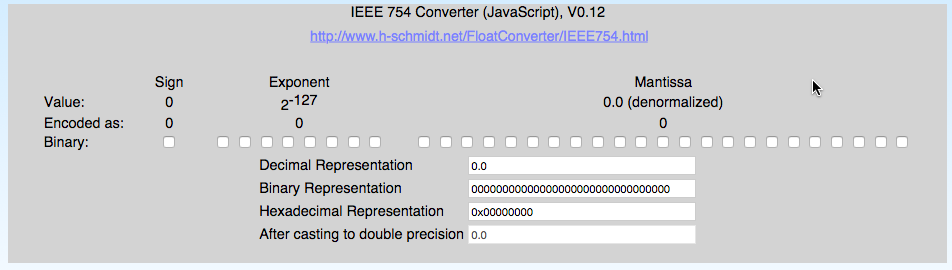
Exercises with the Floating Point Converter

Does this applet support NaN, and ∞?
Are there several different representations of +∞?
What is the largest float representable with the 32-bit format?
What is the smallest normalized float (i.e. a float which has an implied leading 1. bit)?
What is the smallest unnormalized float (when the leading 1. is not implied)?

Unexpected Results with Floating Point arithmetic

This example is taken from Lahey's page.

// FloatingPointStrange3.java
// taken from http://www.lahey.com/float.htm

class FloatingPointStrange3 {
   
    
    public static void main( String args[] ) {
	float x, y, y1, z, z1;

	x = 77777.0f;
	y = 7.0f;
	y1 = 1.0f / y;
	z = x / y;
	z1 = x * y1;
	
	if ( z != z1 ) {
	    System.out.println( String.format( "%1.3f != %1.3f", z, z1 ) );
	    System.out.println( String.format( "%1.30f != %1.30f", z, z1 ) );
	}
	else {
	    System.out.println( String.format( "%1.3f == %1.3f", z, z1 ) );
	    System.out.println( String.format( "%1.30f == %1.30f", z, z1 ) );
	}
			    
    }
}

Output

If we compile and run the java program above, we get this output:

$ javac FloatingPointStrange3.java
$ java FloatingPointStrange3
11111.000 != 11111.001
11111.000000000000000000000000000000 != 11111.000976562500000000000000000000

Notice that the two numbers which mathematically should be correct, aren't in 32-bit IEEE format. If we replace the floats by doubles we get:

11111.000 == 11111.000
11111.000000000000000000000000000000 == 11111.000000000000000000000000000000

Different results depending on the precision selected. With single precision, the result is inexact. With double precision it is mathematically exact!

Check out this page for the same example in C++.

Programming with Floating-Point Numbers in Assembly

Chapter 11 of Randall Hyde's Art of Assembly Language is a good introduction to programming with Floating Point (FP) numbers. Don't miss reading it!

The architecture of the Floating-Point Unit is DIFFERENT!

The definite guide to the Floating Point Unit (FPU) architecture is provided in Section 6-2 of Intel's Pentium Family Developer's Manual, Volume 3.

For us programmers, the main view of the FPU is its 8 80-bit FPU registers organized as a stack. The registers can be accessed directly, but most often are used as a stack. This stack in internal to the processor, not in memory. Imagine that these registers are on top of each other, and that when you push a new value in the top register, all the values are pushed down the stack of registers, automatically. The idea is to push down floating point numbers in the stack, and when an operation such as add or multiply is issued to the stack, the top two values in the stack are popped out, combined together using the operator, and the result is pushed back in the stack. This stack inside the processing unit is the basis for the reverse polish notation (RPN) used in some early calculators, such as the HP calculators.

Here is an example of how one would key in the sequence of numbers of operators to solve the expression (7+10)/9

number/operator entered by user	ST[0] (top)	ST[1]	ST[2]	ST[3]
7	7	.	.	.
10	10	7	.	.
+	17	.	.	.
9	9	17	.	.
/	1.88889	.	.	.

In the Pentium, the 8 registers are either called R0, R1, ... R8, or also ST[0], ST[1], ... ST[7], where ST[i] means the i^th register from the top of the stack, with ST[0] representing the top. For simplicity of notation, Intel refers to ST[0] as ST.

Besides the floating-point registers, the FPU also supports other registers, including a status register used to track special conditions resulting from floating-point operations.

Instructions

Our goal here is to provide a simplified introduction to the FPU, and not a full coverage of all the instructions. We cover only a few instructions of Intel's 6 categories of instructions, enough to illustrate the behavior of the FPU with a few simple assembly language programs later. Check here for additional instructions.

Data Transfer Instructions
Nontranscendental Instructions
Comparison Instructions
Transcendental Instructions
Constant Instructions
Control Instructions

The classification below is taken from M. Mahoney at cs.fit.edu.

Move

Instruction	Information
fld x	push real4, real8, tbyte, convert to tbyte
fild x	push integer word, dword, qword, convert to tbyte
fst x	convert ST and copy to real4, real8, tbyte
fist x	convert ST and copy to word, dword, qword
fstp x	convert to real and pop
fistp x	convert to integer and pop
fxch st(n)	swap with st(0)

Qword integer operands are only valid for load and store, not arithmetic.

Arithmetic

Operands can be signed integers (word or dword), or floating point (real4, real8 or tbyte). All arithmetic is tbyte (80 bits) internally.

Instruction	Information
fadd	add st(0) to st(1) and pop (result now in st(0))
fadd st, st(n)	add st(1)-st(7) to st(0)
fadd st(n), st	add st(0) to st(1-7)
faddp st(n), st	add to st(n) and pop
fadd x	add real x to st
fiadd x	add integer word or dword x to st
fsub, fisub	subtract real, integer
fsubr, fisubr	subtract in reverse: st(1) = st-st(1), pop
fmul, fimul	multiply
fdiv, fidiv	divide
fdivr, fidivr	divide in reverse
fsubp, fsubrp, fmulp, fdivp, fdivrp	pop like faddp

The following instructions have no explicit operands but push constants in the stack.

Instruction	Comment
fldz	push 0
fld1	push 1
fldpi	push pi
fldl2e	push log2(e)
fldl2t	push log2(10)
fldlg2	push log10(2)
fldln2	push ln(2)

The following instructions replace the stack register with the result.

Instruction	Comment
fabs	st = abs(st)
fchs	st = -st
frndint	round to integer (depends on rounding mode)
fsqrt	square root
fcos	cosine (radians)
fsin	sine
fsincos	sine, then push cosine
fptan	tangent
fpatan	st(1) = arctan(st(1)/st), pop

The following instuctions can be combined to compute exponents.

Instruction	Comment
fxtract	pop st, push exponent, mantissa parts
fscale	st *= pow(2, (int)st(1)) (inverse of fxtract)
f2xm1	pow(2, st) - 1, -1 <= st <= 1
fyl2x	st(1) *= log2(st), pop
fyl2xp1	st(1) = st(1) * log2(st) + 1, pop

Compare

The comparison sets carry and zero flags, and parity for undefined (NaN) comparisons.

Instruction	Information
fcom x	compare (operands like fadd), set flags C0-C3
fnstsw ax	copy flags to AX
sahf	copy AH to flags
ja, je, jne, jb	test CF, ZF flags as if for unsigned int compare
fcomp, fcompp	compare and pop once, twice
ficom x	compare with int
ficomp	compare with int, pop
fcomi	compare, setting CF, ZF directly (.686)
fcomip	compare direct and pop (.686)
fucom, fucomp, fucompp	compare allowing unordered (NaN) without interrupt
fucomi, fucomip	compare setting CF, ZF, PF directly (.686)
jp	test for unordered compare (parity flag)
ftst	compare st with 0

Assembly Language Programs

Adding 2 Floats

Printing floats is not an easy to do in assembly, except if we use the standard C libraries to print them. The programs below use such an approach. The way it works is that we call the printf( ... ) function from within the program by first telling nasm that printf is a global function, and then using gcc instead of ld to generate the executable. To print a 64-bit float variable called temp in C we would write:

        printf( "z = %e\n", temp );

So when we want to print z from assembly, we pass the address of the string "temp = %e\n" in the stack, followed by 2 double words representing the value of temp. This is illustrated below in this example where we take two floats x and y equal to 1.5 and 2.5, respectively, and we add them together and store the result in z. Note here that we create two variables that contain the sum, one that is 32-bit in length, z, and one that is 64 bits in length (temp), which is what the printf() function needs.

; sumFloat.asm   use "C" printf on float
; 
; Assemble:	nasm -f elf sumFloat.asm
; Link:		gcc -m32 -o sumFloat sumFloat.o
; Run:		./sumFloat
; prints a single precision floating point number on the screen
; This program uses the external printf C  function which requires
; a format string defining what to print, and a variable number of
; variables to print.


        extern printf                   ; the C function to be called

        SECTION .data                   ; Data section

msg     db      "sum = %e",0x0a,0x00
x	dd	1.5
y	dd	2.5
z	dd	0
temp	dq	0
	
	
        SECTION .text                   ; Code section.

        global	main		        ; "C" main program 
main:				        ; label, start of main program
	
	fld	dword [x]	        ; need to convert 32-bit to 64-bit
	fld	dword [y]
	fadd
	fstp	dword [z]		; store sum in z


	fld	dword [z]     		; transform z in 64-bit word by pushing in stack
	fstp	qword [temp]            ; and popping it back as 64-bit quadword

		 
	push	dword [temp+4] 		; push temp as 2 32-bit words
	push	dword [temp]
        push    dword msg		; address of format string
        call    printf			; Call C function
        add     esp, 12			; pop stack 3*4 bytes

        mov     eax, 1			; exit code, 0=normal
	mov	ebx, 0
        int	0x80			;

Computing an Expression

The next program computes z = (x-1) * (y+3.5), where x is 1.5 and y is 2.5. This program also uses the external printf C function to display the value of z.

; 
; Assemble:	nasm -f elf float1.asm
; Link:		gcc -m32 -o float1 float1.o
; Run:		./float1
; Compute z = (x-1) * (y+3.5), where x is 1.5 and y is 2.5
; This program uses the external printf C  function which requires
; a format string defining what to print, and a variable number of
; variables to print.
%include "dumpRegs.asm"

        extern printf                   ; the C function to be called

        SECTION .data                   ; Data section

msg     db      "sum = %e",0x0a,0x00
x	dd	1.5
y	dd	2.5
z	dd	0
temp	dq	0
	
	
        SECTION .text                   ; Code section.

        global	main		        ; "C" main program 
main:				        ; label, start of main program

;;; compute x-1
	fld	dword [x]	        ; st0 <- x
	fld1				; st0 <- 1 st1 <- x
	fsub				; st0 <- x-1

;;; keep (x-1) in stack and compute y+3.5

	fld	dword [y]		; st0 <- y st1 <- x-1
	push	__float32__( 3.5 )	; put 32-bit float 3.5 in memory (actually in stack)
	fld	dword [esp]		; st0 <- 3.5 st1 <- y st2 <- x-1
	add	esp, 4			; undo push
	fadd				; st0 <- y+3.5 st1 <- x-1
	
	fadd				; st0 <- x-1 + y+3.5
	fst	dword [z]		; store sum in z


	fld	dword [z]     		; transform z in 64-bit word
	fstp	qword [temp]            ; store in 64-bit temp and pop stack top

		 
	push	dword [temp+4] 		; push temp as 2 32-bit words
	push	dword [temp]
        push    dword msg		; address of format string
        call    printf			; Call C function
        add     esp, 12			; pop stack 3*4 bytes

        mov     eax, 1			; exit code, 0=normal
	mov	ebx, 0
        int	0x80			;

Notes

The fld instruction cannot load an immediate value in the FPU. So we push the immediate value in the regular stack controlled by esp, and then from the stack into the FPU using fld.

Computing the Sum of an Array of Floats

; sumFloat4.asm   use "C" printf on float
; D. Thiebaut
; Assemble:	nasm -f elf sumFloat4.asm
; Link:		gcc -m32 -o sumFloat4 sumFloat4.o
; Run:		./sumFloat4
;
; Compute the sum of all the values in the array table.


        extern printf                   ; the C function to be called

        SECTION .data                   ; Data section
	
table		dd		 7.36464646465
		dd		 0.930984158273
		dd		 10.6047098049
		dd		 14.3058722306
		dd		 15.2983812149
		dd		 -17.4394255035
		dd		 -17.8120975978
		dd		 -12.4885670266
		dd		 3.74178604342
		dd		 16.3611827165
		dd		 -9.1182728262
		dd		 -11.4055038727
		dd		 4.68148165048
		dd		 -9.66095817322
		dd		 5.54394454154
		dd		 13.4203706426
		dd		 18.2194407176
		dd		 -7.878340987
		dd		 -6.60045833452
		dd		 -7.98961850398
N		equ		($-table)/4 	; number of items in table
	
;;; sum of all the numbers in table =  10.07955736
	
msg     db      "sum = %e",0x0a,0x00
temp	dq	0
sum	dd	0	
	
        SECTION .text                   ; Code section.

        global	main		        ; "C" main program 
main:				        ; label, start of main program

	mov	ecx, N
	mov	ebx, 0

	fldz				; st0 <- 0
for:	fld	dword [table + ebx*4]	; st0 <- new value, st1 <- sum of previous
	fadd				; st0 <- sum of new plus previous sum
	inc	ebx
	loop	for

;;; get sum back from FPU
	fstp	dword [sum]   		; put final sum in variable

;;; print resulting sum
	fld	dword [sum]    		; transform z in 64-bit word
	fstp	qword [temp]            ; store in 64-bit temp and pop stack top

		 
	push	dword [temp+4] 		; push temp as 2 32-bit words
	push	dword [temp]
        push    dword msg		; address of format string
        call    printf			; Call C function
        add     esp, 12			; pop stack 3*4 bytes

        mov     eax, 1			; exit code, 0=normal
	mov	ebx, 0
        int	0x80			;

Output

  sum = 1.007956e+01

Finding the Largest Element of an Array of Floats

; sumFloat5.asm   use "C" printf on float
; D. Thiebaut
; Assemble:	nasm -f elf sumFloat5.asm
; Link:		gcc -m32 -o sumFloat5 sumFloat5.o
; Run:		./sumFloat5
; Compute the max of an array of floats stored in table.
; This program uses the external printf C  function which requires
; a format string defining what to print, and a variable number of
; variables to print.


        extern printf                   ; the C function to be called

        SECTION .data                   ; Data section
	
max		dd		 0	
table		dd		 7.36464646465
		dd		 0.930984158273
		dd		 10.6047098049
		dd		 14.3058722306
		dd		 15.2983812149
		dd		 -17.4394255035
		dd		 -17.8120975978
		dd		 -12.4885670266
		dd		 3.74178604342
		dd		 16.3611827165
		dd		 -9.1182728262
		dd		 -11.4055038727
		dd		 4.68148165048
		dd		 -9.66095817322
		dd		 5.54394454154
		dd		 13.4203706426
		dd		 18.2194407176
		dd		 -7.878340987
		dd		 -6.60045833452
		dd		 -7.98961850398
N		equ		($-table)/4 	; number of items in table
	
;; max of all the numbers  = 1.821944e+01
	
msg     db      "max = %e",0x0a,0x00
temp	dq	0

	
        SECTION .text                   ; Code section.

        global	main		        ; "C" main program 
main:				        ; label, start of main program
	mov	eax, dword [table]
	mov	dword [max], eax
	
	mov	ecx, N-1
	mov	ebx, 1

	fld	dword [table]		; st0 <- table[0]
	
for:	fld	dword [table + ebx*4]	; st0 <- new value, st1 <- current max
	fcom				; compare st0 to st1
	fstsw	ax			; store fp status in ax
	and	ax, 100000000b		;
	jz	newMax
	jmp	continue
	
newMax:	fxch	st1
	
continue:
	fcomp				; pop st0 (don't care about compare)

	inc	ebx			; point to next fp number
	loop	for

;;; get sum back from FPU
	fstp	dword [max]   		; st0 is max.  Store it in mem

;;; print resulting sum
	fld	dword [max]    		; transform z in 64-bit word
	fstp	qword [temp]            ; store in 64-bit temp and pop stack top

		 
	push	dword [temp+4] 		; push temp as 2 32-bit words
	push	dword [temp]
        push    dword msg		; address of format string
        call    printf			; Call C function
        add     esp, 12			; pop stack 3*4 bytes

        mov     eax, 1			; exit code, 0=normal
	mov	ebx, 0
        int	0x80			;