CSC270 Midterm Prep 2012
--D. Thiebaut 08:40, 9 March 2012 (EST)
Below are some problems that will help you prepare for the midterm.
- Assume you have a boolean function f defined as:
- f = Σ(1,3,5).
- Give the maxterm canonical form of f.
- Implement f above with NANDs only. With NORs only.
- Assume that you have a desk with 3 drawers and a secret compartment. The drawers have electronic sensors that detect if a drawer is open (1) or closed (0). We want to build a simple circuit that will activate a release signal (set it to 1) to open the secret compartment only if the right combination of steps is taken.
- This combination of steps is:
- All drawers are closed
- Drawer 1 is open
- Drawer 1 is closed
- Drawer 3 is open and stays open
- Drawer 2 is open
- Drawer 2 is closed
- At this point the release signal is activated. It stays on as long as none of the drawers moves. The secret compartment opens!
- Question
- How many states does this FSM have?
- Implement the function below with a 4-to-16 decoder. The decoder has active-low outputs and an active-low enable. Be efficient in your design.
- f = Σ(0,1,3,4,5,6,7,8,9,10,11,12,14)
- Implement a 3-to-8 decoder with several 2-to-4 decoders. You may assume that the decoders have
enable inputs, and you are free to choose active-high or active-low signals.
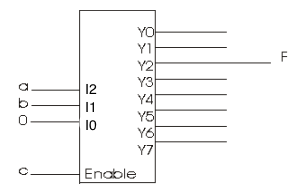
- What is the boolean representation of the function f shown in the figure below? Express f in its
simplest form.
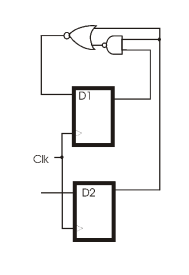
- What is the state diagram of the sequential circuit shown below, if D2 is set to 1 always? If D2 is set to
0 always?