Difference between revisions of "CSC212 Lab 12 2014"
(→Lab Problem #1: Recursion-Stack Depth) |
(→Lab Problem #1: Recursion-Stack Depth) |
||
| Line 8: | Line 8: | ||
</bluebox> | </bluebox> | ||
<br /> | <br /> | ||
| + | <br /> | ||
| + | =Lab Problem #0: Observing Quicksort at Work= | ||
| + | <br /> | ||
| + | * Point your '''Firefox''' or '''Safari''' browser to this URL: [http://cs.smith.edu/~thiebaut/java/sort/ http://cs.smith.edu/~thiebaut/java/sort/]. Chrome won't work with 64-bit Java Applets, so no need to try it... | ||
| + | * You may need to '''resize''' the window or shrink/expand the applet to see the '''Start''' Button. | ||
| + | <br /> | ||
| + | ==Standard Quicksort, Random Array== | ||
| + | <br /> | ||
| + | * Select '''Standard Quicksort''' for the Sorting Algorithm | ||
| + | * Select '''Random''' for the Array Type | ||
| + | * Select '''Swap Square''' for the View | ||
| + | * Delay of 25 | ||
| + | * '''Start!''' | ||
| + | * <font color="magenta">Notice how partition works. Whatever group of bars is red represent the partition that is being split into 2 around the pivot.</font> | ||
| + | * Don't hesitate to run the experiment a few times until you "get it". | ||
| + | <br /> | ||
| + | ==Standard Quicksort, Array in Increasing Order== | ||
| + | <br /> | ||
| + | * Click '''Stop''' so that you can start a new experiment. | ||
| + | * Select '''Standard Quicksort''' for the Sorting Algorithm | ||
| + | * Select '''Sorted Incr. Order''' for the Array Type | ||
| + | * Select '''Swap Square''' for the View | ||
| + | * Delay of 25 | ||
| + | * '''Start!''' | ||
| + | * <font color="magenta">Notice how the partition is of size ''N'' first, then ''N-1'', then ''N-2'', etc.</font> | ||
| + | <br /> | ||
| + | ==Standard Quicksort, Array in Decreasing Order== | ||
| + | <br /> | ||
| + | * Click '''Stop''' so that you can start a new experiment. | ||
| + | * Select '''Standard Quicksort''' for the Sorting Algorithm | ||
| + | * Select '''Sorted Decr. Order''' for the Array Type | ||
| + | * Select '''Swap Square''' for the View | ||
| + | * Delay of 25 | ||
| + | * '''Start!''' | ||
| + | * <font color="magenta">Notice how the partition is of size ''N'' first, then ''N-2'', then ''N-4'', etc.</font> | ||
| + | <br /> | ||
| + | ==Quicksort with a Random Pivot== | ||
| + | <br /> | ||
| + | * Repeat the same experiments above, (random array, sorted in increasing order, sorted in decreasing order), but pick "Quicksort with Random Pivot" as the algorithm. | ||
| + | * Does the random pivot help with the random array? | ||
| + | <br /> | ||
| + | ==Quicksort with Median of Three Pivot== | ||
| + | <br /> | ||
| + | |||
| + | <br /> | ||
| + | ==Quicksort with Tail Recursion Truncated== | ||
| + | <br /> | ||
| + | * Same experiments again, but this time pick the "Quicksort with Tail Recursion Truncated" algorithm. Try to answer the following questions to yourself, as a way of understanding how tail recursion works for Quicksort. Nothing to submit anywhere... | ||
| + | <br /> | ||
| + | ;Question 1: | ||
| + | :Can you see the tail recursion being truncated? Which sorting method is used to sort the small partitions? | ||
| + | ;Question 2: | ||
| + | :Is the O(N^2) sorting routine called on all the small partitions, separately, or is it called on the whole array? | ||
| + | ;Question 3: | ||
| + | :Can you explain the two areas identified below? | ||
| + | <br /> | ||
| + | <center>[[Image:QuicksortTailRecursionCut.png|400px]]</center> | ||
| + | ;Question 4: | ||
| + | :Is the Quicksort algorithm cutting the tail recursion, also using a random pivot or not? | ||
| + | <br /> | ||
| + | <br > | ||
=Lab Problem #1: Recursion-Stack Depth= | =Lab Problem #1: Recursion-Stack Depth= | ||
<br /> | <br /> | ||
Revision as of 15:19, 12 November 2014
--D. Thiebaut (talk) 19:37, 9 November 2014 (EST)
Contents
This lab deals with Sorting algorithms, HeapSort, QuickSort, and methods used to avoid worst-case conditions.
Lab Problem #0: Observing Quicksort at Work
- Point your Firefox or Safari browser to this URL: http://cs.smith.edu/~thiebaut/java/sort/. Chrome won't work with 64-bit Java Applets, so no need to try it...
- You may need to resize the window or shrink/expand the applet to see the Start Button.
Standard Quicksort, Random Array
- Select Standard Quicksort for the Sorting Algorithm
- Select Random for the Array Type
- Select Swap Square for the View
- Delay of 25
- Start!
- Notice how partition works. Whatever group of bars is red represent the partition that is being split into 2 around the pivot.
- Don't hesitate to run the experiment a few times until you "get it".
Standard Quicksort, Array in Increasing Order
- Click Stop so that you can start a new experiment.
- Select Standard Quicksort for the Sorting Algorithm
- Select Sorted Incr. Order for the Array Type
- Select Swap Square for the View
- Delay of 25
- Start!
- Notice how the partition is of size N first, then N-1, then N-2, etc.
Standard Quicksort, Array in Decreasing Order
- Click Stop so that you can start a new experiment.
- Select Standard Quicksort for the Sorting Algorithm
- Select Sorted Decr. Order for the Array Type
- Select Swap Square for the View
- Delay of 25
- Start!
- Notice how the partition is of size N first, then N-2, then N-4, etc.
Quicksort with a Random Pivot
- Repeat the same experiments above, (random array, sorted in increasing order, sorted in decreasing order), but pick "Quicksort with Random Pivot" as the algorithm.
- Does the random pivot help with the random array?
Quicksort with Median of Three Pivot
Quicksort with Tail Recursion Truncated
- Same experiments again, but this time pick the "Quicksort with Tail Recursion Truncated" algorithm. Try to answer the following questions to yourself, as a way of understanding how tail recursion works for Quicksort. Nothing to submit anywhere...
- Question 1
- Can you see the tail recursion being truncated? Which sorting method is used to sort the small partitions?
- Question 2
- Is the O(N^2) sorting routine called on all the small partitions, separately, or is it called on the whole array?
- Question 3
- Can you explain the two areas identified below?
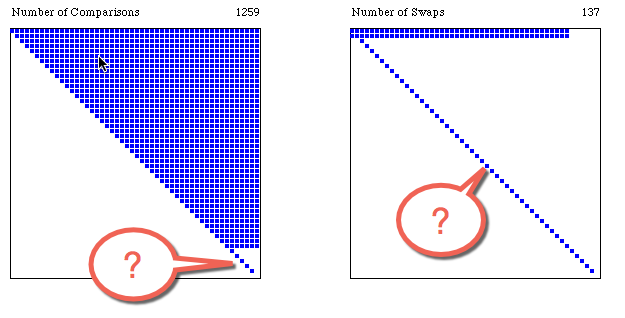
- Question 4
- Is the Quicksort algorithm cutting the tail recursion, also using a random pivot or not?
Lab Problem #1: Recursion-Stack Depth
- Create a class containing the code for Quicksort.
- Run it on arrays of size 10, 200, 500, 1000, 5000, 10000, 50000, 100000. Keep on increasing the size until something happens...
- You probably ran into an exception... Make sure you read what the exception is... Can you figure it out?
- Read the documentation of the -XSS command line on this page.
- Apply it to your program
- If you are using Eclipse, click on the Run top menu-option, then Run Configurations, then on the Arguments tab, and in the VM arguments window, enter something like -Xss4m (you'll have to do go through some trials and errors to find the right value.
- If you are running your Java code on beowulf, simply add the option on the command line for the Java Virtual Machine (in this case, a request for 64 Megabytes of stack size):
java -Xss64m QuickSort 1000000 random
- Make sure you have define a large enough stack to sort at least a million ints.
Lab Problem #2: HeapSort
- Java provides heap data structures, but calls them PriorityQueues.
- Instead of keeping the largest element at the top of the heap, PriorityQueues keep the smallest element at the top.
- Try the example below to see how to use a PriorityQueue
import java.util.PriorityQueue; public static void TestPrioQueues() { PriorityQueue<Integer> heap = new PriorityQueue<Integer>(); heap.add( 1 ); heap.add( 20 ); heap.add( 5 ); heap.add( 100 ); while ( ! heap.isEmpty() ) System.out.println( heap.poll() ); }
- Question 1
- Using some of the code/functions from this page, create a function called heapsort( int[] A ) that will use a priority queue to sort the array of ints A.
- Question 2
- Using the code snippet below, measure the execution times of QuickSort and of your HeapSort function. Figure out which is regularly faster on arrays of varying sizes.
long start = System.nanoTime(); quicksort(A, 0, A.length - 1); long end = System.nanoTime(); System.out.println( String.format( "quickSort( %d ) takes %1.3f msec", N, (end-start)/1000000.0f ) );
Lab Problem #3: Speeding Up QuickSort
- You should have gone through Problem #2 and modified QuickSort so that you can measure its execution time.
- Name your file Lab12_3.java, and your class Lab12_3 (you will need to submit it to Moodle).
- Run it on sorted arrays of varying sizes until you find an array size that requires between 1 and 10 seconds of execution time.
- Pick one of the methods we saw in class for allowing Quicksort to avoid worst case conditions, and implement it. Modify your code.
- Verify that you have seriously improved your Quicksort function with this mod.
Moodle Submission
- Submit your program to Moodle. Your program will be run against the solution program on a sorted array. The grade is proportional to how close your execution time comes to the execution time of the solution program.

