CSC111 Homework 12 2015

--D. Thiebaut (talk) 17:30, 19 April 2015 (EDT)

---

<showafterdate after="20150422 14:00" before="20150601 00:00">

This homework is optional. If you skip it, you will not be penalized. If you work on it and submit it, however, the grade you will get for will replace the lowest grade you will have obtained on any of the previous homework assignments. So, if you were not able to submit Homework 5, for example, then the grade for Homework 12 will become the grade for Homework 5.
The rule of dropping the lowest homework of the semester still holds. Once the grade for Homework 12 is plugged into your past homework grades, I will drop the lowest of the whole semester. This will not be apparent in the grade-book on Moodle, but will be done in an eXcel spreadsheet, once the semester is over.

Problem #1

Write a program called hw12_1.py that contains a recursive function called smallestLargest() which returns the smallest and largest elements of a list of items. The items may be strings, numbers, or tuples, where the first element of the tuple is either a number or a string.

Example main() program:

def main():
     A = [ 1, 10, 20, 3, 2, -1, -10, 5, 5, 5, 5 ]
     low, high = smallestLargest( A )
     print( "smallest item =", low, " largest item = ", high )
     # will print
     # smallest item = -10 largest item = 20

     A = [ 1 ]
     low, high = smallestLargest( A )
     print( "smallest item =", low, " largest item = ", high )
     # will print
     # smallest item = 1 largest item = 1
 
     A = [ ]
     low, high = smallestLargest( A )
     print( "smallest item =", low, " largest item = ", high )
     # will print
     # smallest item = None largest item = None

     A = [ "alpha", "beta", "gamma", "epsilon" ]
     low, high = smallestLargest( A )
     print( "smallest item =", low, " largest item = ", high )
     # will print
     # smallest item = alpha largest item = gamma

if __name__=="__main__":
     main()

Requirements

1. The function smallestLargest() must be recursive.
2. You cannot use the min() or max() standard Python functions. If you want to find the largest of two items, you need to do the comparison in Python, using <, <=, >, or >=.

Submission

Submit your program to the Moodle section, HW12 PB 1

Problem #2

Write a Python program called hw12_2.py that generates, recursively a tree with fruit, as close to the tree shown below as possible. You should not reproduce the text in the image; just the tree, its colors, and its fruit.

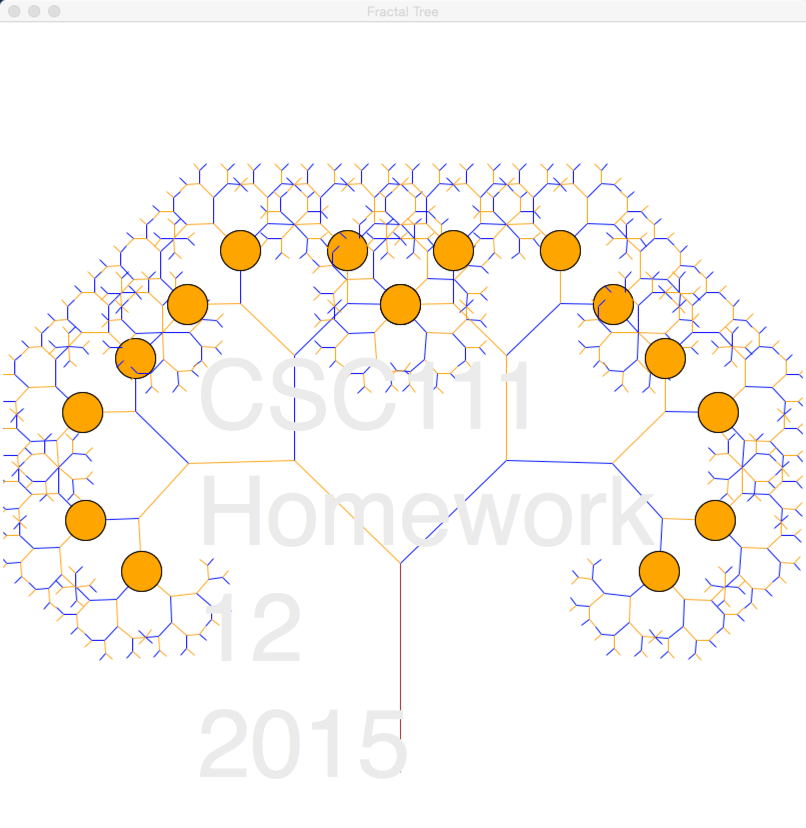
Requirements

• The oranges have a radius of 20. They must be generated inside the recursive function. As a result some of the branches will appear in front, some below the oranges.
• The branches must have different colors, and not be all drawn with the same color.

Submission

• Submit your program as well as a screen capture of its output to Moodle, in the HW12 PB2 and HW12 Image 2 sections.
• Note: To change the color of a line with the graphics library (use graphics111.py, please), you should use the setOutline() method rather than the setFill() method.
• I used only 3 colors to generate the tree above: "orange", "blue", and "brown".

</showafterdate>

<showafterdate after="20150429 00:00" before="20150601 00:00">

Solution Programs

Recursive MinMax

# hw12_1.py
# D. Thiebaut
# Solution program for Homework 12

def minmax( A ):
    """recursive function that returns the min and max of a list
    of comparable items"""

    # stopping condition #1
    if len( A )==0:
        return None, None

    # stopping condition #2
    if len( A )==1:
        return A[0], A[0]

    # recursive step
    theMin, theMax = minmax( A[1: ] )

    # do a bit of work...
    if A[0] < theMin:
        theMin = A[0]
    if A[0] > theMax:
        theMax = A[0]

    # return the smallest or largest of what we kept
    # and what the recursive call brought back
    return theMin, theMax

def main():
     A = [ 1, 10, 20, 3, 2, -1, -10, 5, 5, 5, 5 ]
     low, high = minmax( A )
     print( "smallest item =", low, " largest item = ", high )
     # will print
     # smallest item = -10 largest item = 20

     A = [ 1 ]
     low, high = minmax( A )
     print( "smallest item =", low, " largest item = ", high )
     # will print
     # smallest item = 1 largest item = 1
 
     A = [ ]
     low, high = minmax( A )
     print( "smallest item =", low, " largest item = ", high )
     # will print
     # smallest item = None largest item = None

     A = [ "alpha", "beta", "gamma", "epsilon" ]
     low, high = minmax( A )
     print( "smallest item =", low, " largest item = ", high )
     # will print
     # smallest item = alpha largest item = gamma

if __name__=="__main__":
     main()

Fractal Tree

# fractalTree.py
# D. Thiebaut
# Code taken from http://openbookproject.net/thinkcs/python/english3e/recursion.html
# and adapted to work with graphics111.py.
#
# Draws a fractal tree on the graphic window.
#
from graphics import *
import math
import time
import random

# dimensions of the window
MAXWIDTH = 800
MAXHEIGHT = 800

# recursive tree-drawing function
# 
def draw_tree(win   ,       # the canvas
              order,        # the level of recursion.  Starts positive.
              theta,        # angle of new branch leaving this trunk
              sz,           # size of this branch
              x, y,         # coordinates of base of this branch
              heading,      # angle of direction of this branch
              color         # color
              ):    

   trunk_ratio = 0.29       # How big is the trunk relative to whole tree?
   trunk = sz * trunk_ratio # length of trunk

   # compute x, y of end of the current branch
   delta_x = trunk * math.cos(heading)
   delta_y = trunk * math.sin(heading)
   x2, y2 = x + delta_x, y + delta_y

   
   # draw current branch
   branch = Line( Point( x, y), Point( x2, y2 ) )
   branch.setFill( color )
   branch.setWidth( 2 )
   branch.setOutline( color )
   branch.draw( win )

   # if this branch has sub-branches, then recurse
   if order > 0:    
       
      # make the recursive calls to draw the two subtrees
      newsz = sz*(1 - trunk_ratio)
      draw_tree(win,
                order-1, theta, newsz, x2, y2, heading-theta,
                "orange" )
      draw_tree(win,
                order-1, theta, newsz, x2, y2, heading+theta,
                "blue" )
      
   # draw orange
   if order == 4:
       orange = Circle( Point( x, y ), 20 )
       orange.setFill( "orange" )
       orange.draw( win )


# draw 1 tree in the middle of the screen, shooting straight up.
def main():
    win = GraphWin("Fractal Tree", MAXWIDTH, MAXHEIGHT )
    theta = 0.8      # use 0.02 for tall skinny trees, 0.7 for fat trees
    draw_tree(win,
              9,
              theta,
              MAXWIDTH*0.9, MAXWIDTH//2,
              MAXHEIGHT-50,
              -math.pi/2,
              "brown" )
        
    win.getMouse()
    win.close()

main()

</showafterdate>

...