Difference between revisions of "CSC103 The Limits of Computers: Outline"
(→The bottleneck) |
(→References) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 53: | Line 53: | ||
<br /> | <br /> | ||
| − | <center>[[Image:SoccerField. | + | <center>[[Image:SoccerField.jpg]]</center> |
<br /> | <br /> | ||
| Line 83: | Line 83: | ||
::In a fascinating paper published in the 31 August, 2000 issue of Nature, Seth Lloyd argued that some interesting limits on computers can be found from the knowledge of the speed of light, c (2.9979 * 10 8 m/s), Plank’s reduced constant, (1.0545 * 10-34 J s), Boltzmann’s constant kb( 1.3805 * 10-23 J/K), the gravitational constant G (6.673 * 10-11 m3 kg-1 s-2), and the application of some of the basic concepts of quantum mechanics and thermodynamics. As an example, Lloyd explores what effect these limits would have on what he terms an 'ultimate laptop' - a computer massing 1 kg, and occupying a volume of 1 liter. | ::In a fascinating paper published in the 31 August, 2000 issue of Nature, Seth Lloyd argued that some interesting limits on computers can be found from the knowledge of the speed of light, c (2.9979 * 10 8 m/s), Plank’s reduced constant, (1.0545 * 10-34 J s), Boltzmann’s constant kb( 1.3805 * 10-23 J/K), the gravitational constant G (6.673 * 10-11 m3 kg-1 s-2), and the application of some of the basic concepts of quantum mechanics and thermodynamics. As an example, Lloyd explores what effect these limits would have on what he terms an 'ultimate laptop' - a computer massing 1 kg, and occupying a volume of 1 liter. | ||
::Eq.5 predicts a maximum memory space of 2.13*10^31 bits. This in turn means that if such an ultimate computer uses all of its memory, it will be able to perform approximately 10^19 operations per bit per second. | ::Eq.5 predicts a maximum memory space of 2.13*10^31 bits. This in turn means that if such an ultimate computer uses all of its memory, it will be able to perform approximately 10^19 operations per bit per second. | ||
| − | ::The amount of information that can be stored by the ultimate laptop, ~ | + | ::The amount of information that can be stored by the ultimate laptop, ~10^31 bits, is much higher than the ~10^10 bits stored on current laptops. This is because conventional laptops use many degrees of freedom to store a bit, whereas the ultimate laptop uses just one. There are considerable advantages to using many degrees of freedom to store information, stability and controllability being perhaps the most important. Indeed, as the above calculation indicates, to take full advantage of the memory space available, the ultimate laptop must turn all of its matter into energy. A typical state of the ultimate laptop's memory looks like a plasma at a billion degrees Kelvin - like a thermonuclear explosion or a little piece of the Big Bang! Clearly, packaging issues alone make it unlikely that this limit can be obtained, even setting aside the difficulties of stability and control. |
Latest revision as of 09:39, 6 March 2011
Contents
Outline
lin scale/log scale

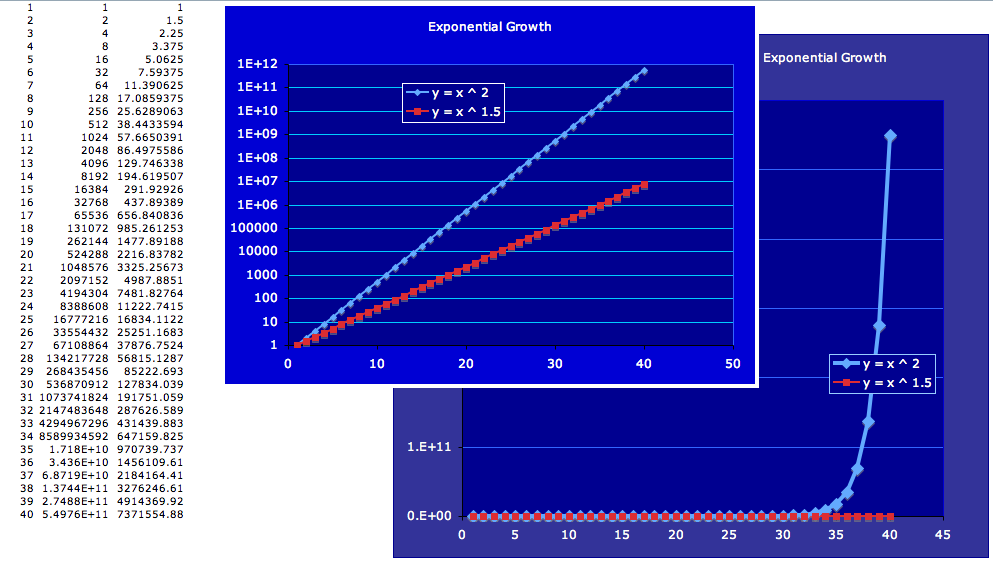
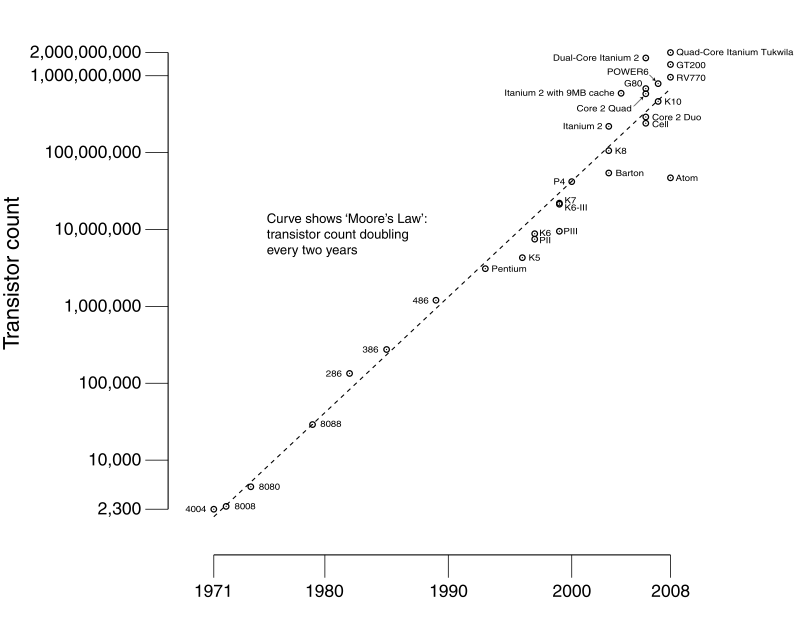
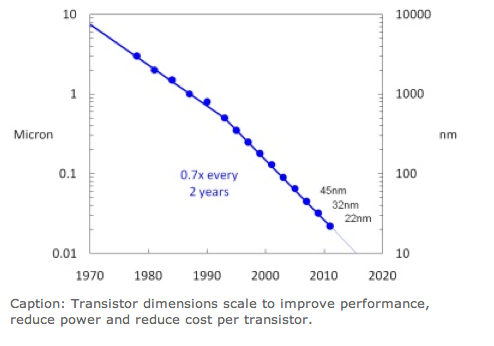
Moore's Law
Various Moore Laws
Transistor Count
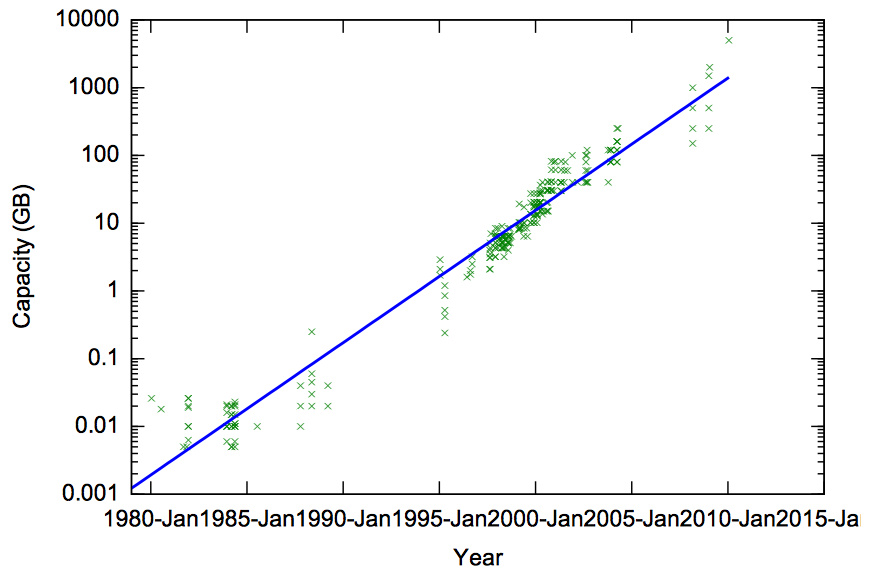
Capacity of Hard Disk
- Intel: www.intel.com/technology/mooreslaw/
Pixels Per Dollar
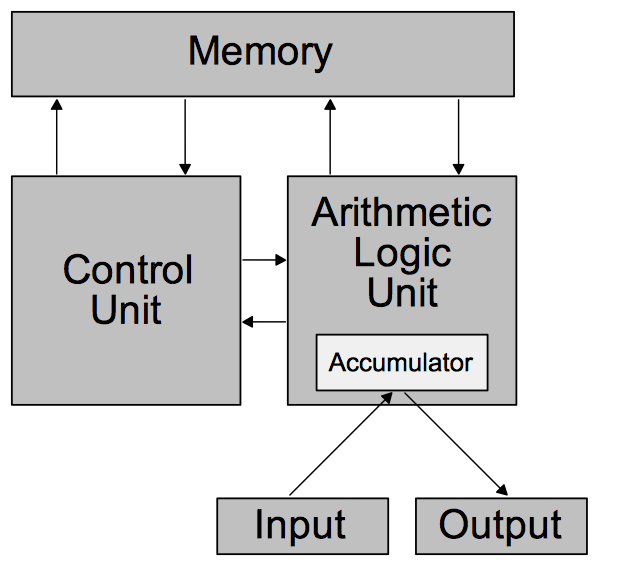
Von Neumann Architecture
- Von Neumann J., First Draft of a Report on the EDVAC, Moore School of Electrical Engineering, University of Pennsylvania, June 30, 1945. (Especially interesting are the first 5 pages)

- Architecture
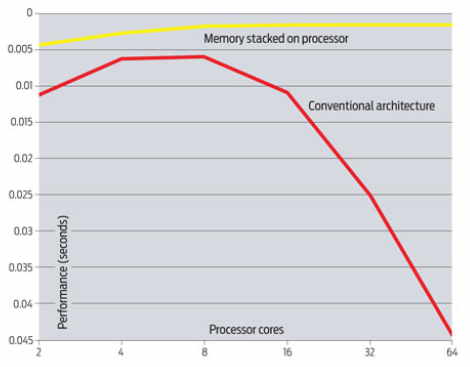
The bottleneck




Physical Limitations
- Power
- Power density increases with density of logic and clock speed
- Dissipating heat
- RC delay
- Speed at which electrons flow limited by resistance and capacitance of metal wires connecting them
- Delay increases as RC product increases
- Wire interconnects thinner, increasing resistance
- Wires closer together, increasing capacitance
- Memory latency
- Memory speeds lag processor speeds
- Solution:
- More emphasis on organizational and architectural approaches
Tricks
- Caching
- Pipelines
- Speculative Execution
Speed
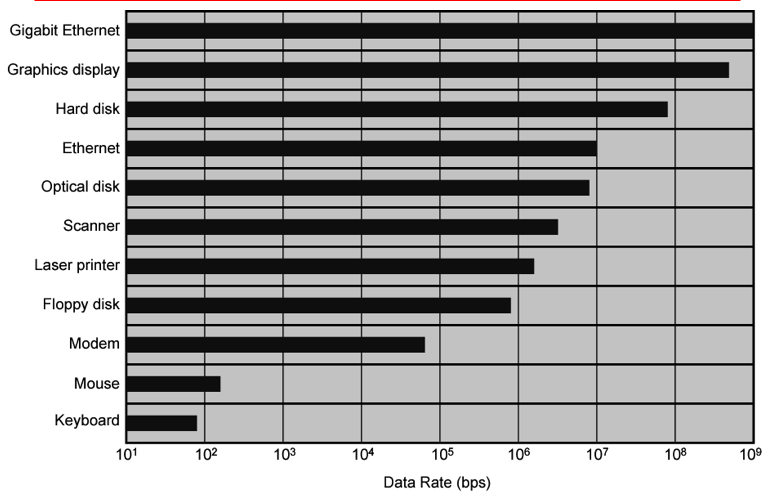
References
- The Ulitmate Limits of Computer, Geon, ArsTechnica, http://arstechnica.com/wankerdesk/01q2/limits/limits-1.html
- In a fascinating paper published in the 31 August, 2000 issue of Nature, Seth Lloyd argued that some interesting limits on computers can be found from the knowledge of the speed of light, c (2.9979 * 10 8 m/s), Plank’s reduced constant, (1.0545 * 10-34 J s), Boltzmann’s constant kb( 1.3805 * 10-23 J/K), the gravitational constant G (6.673 * 10-11 m3 kg-1 s-2), and the application of some of the basic concepts of quantum mechanics and thermodynamics. As an example, Lloyd explores what effect these limits would have on what he terms an 'ultimate laptop' - a computer massing 1 kg, and occupying a volume of 1 liter.
- Eq.5 predicts a maximum memory space of 2.13*10^31 bits. This in turn means that if such an ultimate computer uses all of its memory, it will be able to perform approximately 10^19 operations per bit per second.
- The amount of information that can be stored by the ultimate laptop, ~10^31 bits, is much higher than the ~10^10 bits stored on current laptops. This is because conventional laptops use many degrees of freedom to store a bit, whereas the ultimate laptop uses just one. There are considerable advantages to using many degrees of freedom to store information, stability and controllability being perhaps the most important. Indeed, as the above calculation indicates, to take full advantage of the memory space available, the ultimate laptop must turn all of its matter into energy. A typical state of the ultimate laptop's memory looks like a plasma at a billion degrees Kelvin - like a thermonuclear explosion or a little piece of the Big Bang! Clearly, packaging issues alone make it unlikely that this limit can be obtained, even setting aside the difficulties of stability and control.