Difference between revisions of "Tutorial: Binary Matcher with TensorFlow"
| (7 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
| style="width: 60%;" | | | style="width: 60%;" | | ||
<bluebox> | <bluebox> | ||
| − | This page illustrates how to design a simple multi-layer Tensorflow Neural Net to recognize integers | + | This page (which started as a Jupyter notebook) illustrates how to design a simple multi-layer Tensorflow Neural Net to recognize integers |
coded in binary and output them as a 1-hot vector. | coded in binary and output them as a 1-hot vector. | ||
| Line 22: | Line 22: | ||
<br /> | <br /> | ||
| − | + | ||
<br /> | <br /> | ||
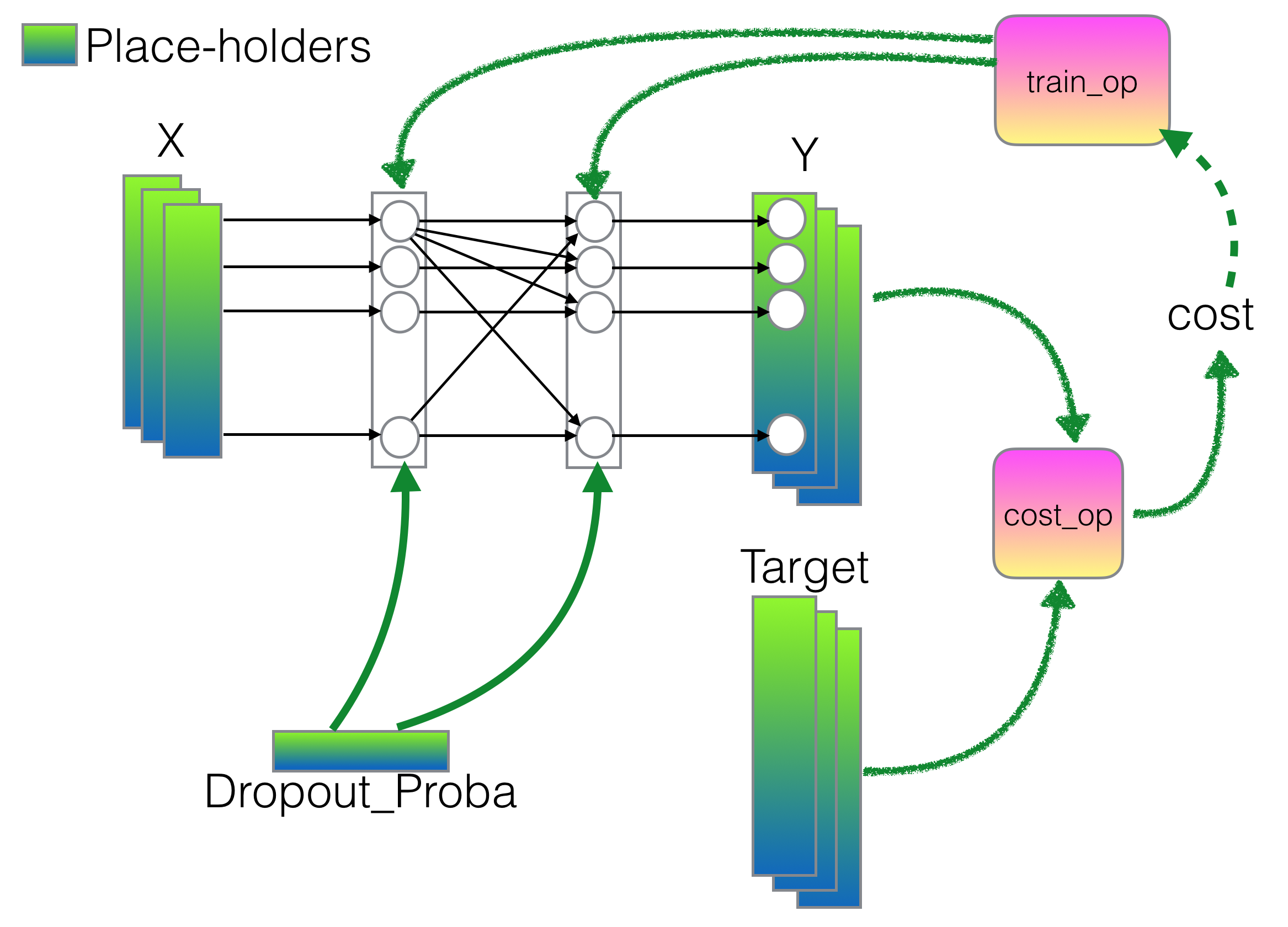
| − | [[Image:TensorFlowBitMatcherDiagram. | + | [[Image:TensorFlowBitMatcherDiagram.png|600px|center]] |
<br /> | <br /> | ||
| − | + | ||
<br /> | <br /> | ||
=Source Files= | =Source Files= | ||
| Line 75: | Line 75: | ||
</source> | </source> | ||
<br /> | <br /> | ||
| − | =Addition of Random Bits= | + | ==Addition of Random Bits== |
<br /> | <br /> | ||
Let's add some random bits (say 7) to the rows of x, and create a larger collection of rows, say 100. | Let's add some random bits (say 7) to the rows of x, and create a larger collection of rows, say 100. | ||
| Line 103: | Line 103: | ||
</source> | </source> | ||
<br /> | <br /> | ||
| − | =Split Into Training and Testing= | + | ==Split Into Training and Testing== |
<br /> | <br /> | ||
We'll split the 100 rows in 90 rows of training, and 10 rows for testing. | We'll split the 100 rows in 90 rows of training, and 10 rows for testing. | ||
| Line 133: | Line 133: | ||
</source> | </source> | ||
<br /> | <br /> | ||
| − | =Package Xs and Ys as Numpy Arrays= | + | ==Package Xs and Ys as Numpy Arrays== |
<br /> | <br /> | ||
We now make the train and test arrays into numpy arrays. | We now make the train and test arrays into numpy arrays. | ||
| Line 175: | Line 175: | ||
</source> | </source> | ||
<br /> | <br /> | ||
| − | ==Place-Holders | + | ==Place-Holders== |
| + | <br /> | ||
It will have place holders for | It will have place holders for | ||
* the X input | * the X input | ||
* the Y target. That's the vectors of Y values we generated above. The network will generate its own version of y, which we'll compare to the target. The closer the two are, the better. | * the Y target. That's the vectors of Y values we generated above. The network will generate its own version of y, which we'll compare to the target. The closer the two are, the better. | ||
| − | * the drop-probability, which is defined as the "keep_probability", i.e. the probability a node from the | + | * the drop-probability, which is defined as the "keep_probability", i.e. the probability a node from the neural net will be kept in the computation. A value of 1.0 indicates that all the nodes are used in the processing of data through the network. |
| − | neural net will be kept in the computation. A value of 1.0 indicates that all the nodes are used in the | ||
| − | processing of data through the network. | ||
<br /> | <br /> | ||
::<source lang="python"> | ::<source lang="python"> | ||
| Line 189: | Line 188: | ||
</source> | </source> | ||
<br /> | <br /> | ||
| + | |||
==Variables== | ==Variables== | ||
<br /> | <br /> | ||
| Line 225: | Line 225: | ||
<br /> | <br /> | ||
::<source lang="python"> | ::<source lang="python"> | ||
| − | #prediction = tf.reduce_sum( tf.mul( tf.nn.softmax( y ), target ), | + | #prediction = tf.reduce_sum( tf.mul( tf.nn.softmax( y ), target ), reduction_indices=1 ) |
| − | |||
#accuracy = tf.reduce_mean ( prediction ) | #accuracy = tf.reduce_mean ( prediction ) | ||
| − | #cost_op = tf.reduce_mean( tf.sub( 1.0, tf.reduce_sum( tf.mul( y, target | + | #cost_op = tf.reduce_mean( tf.sub( 1.0, tf.reduce_sum( tf.mul( y, target ), reduction_indices=1 ) ) ) |
| − | |||
#cost_op = tf.reduce_mean( | #cost_op = tf.reduce_mean( | ||
| − | # tf.sub( 1.0, tf.reduce_sum( tf.mul( target, tf.nn.softmax | + | # tf.sub( 1.0, tf.reduce_sum( tf.mul( target, tf.nn.softmax(y) ), reduction_indices=[1] ) ) |
| − | (y) ), reduction_indices=[1] ) ) | ||
# ) | # ) | ||
# The cost_op below yields an ccuracy on training data of 0.86% and an a | # The cost_op below yields an ccuracy on training data of 0.86% and an a | ||
ccuracy on test data = 0.49% | ccuracy on test data = 0.49% | ||
# for 1000 epochs and a batch size of 10. | # for 1000 epochs and a batch size of 10. | ||
| − | cost_op = tf.reduce_mean( | + | cost_op = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits( labels = target, |
| − | + | logits = y ) ) | |
| − | y ) ) | ||
</source> | </source> | ||
<br /> | <br /> | ||
| Line 250: | Line 246: | ||
</source> | </source> | ||
<br /> | <br /> | ||
| + | |||
=Initialization Phase= | =Initialization Phase= | ||
<br /> | <br /> | ||
| Line 278: | Line 275: | ||
accuracy = tf.reduce_mean ( tf.cast( prediction, tf.float32 ) ) | accuracy = tf.reduce_mean ( tf.cast( prediction, tf.float32 ) ) | ||
for epoch in range( 10000 ): | for epoch in range( 10000 ): | ||
| − | + | for i in range( 0, train_size, batchSize ): | |
| − | + | xx = x_train_np[ i:i+batchSize, : ] | |
| − | + | yy = y_train_np[ i:i+batchSize, : ] | |
| − | + | sess.run( train_op, feed_dict={x: xx, target: yy} ) | |
| + | |||
| + | if epoch%100 == 0: | ||
| + | co, to = sess.run( [cost_op,train_op], feed_dict={x: x_train_np, target: y_train_np} ) | ||
| + | print( epoch, "cost =", co, end=" " ) | ||
| + | accuracyNum = sess.run( accuracy, feed_dict={x: x_train_np, target : y_train_np} ) | ||
| + | print( "Accuracy on training data = %1.2f%%" % (accuracyNum*100), end = " " ) | ||
| + | accuracyNum = sess.run( accuracy, feed_dict={ x: x_test_np, target : y_test_np} ) | ||
| + | print( "Accuracy on test data = %1.2f%%" % ( accuracyNum*100 ) ) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
if False: | if False: | ||
| − | + | print( "y = ", sess.run( y, feed_dict={ x: x_train_np, target : y_train_np} ) ) | |
| − | + | print( "softmax(y) = ", sess.run( tf.nn.softmax( y ), feed_dict={ x: x_train_np, target : y_train_np} ) ) | |
| − | + | print( "tf.mul(tf.nn.softmax(y), target) = ", | |
| − | x_train_np, target : y_train_np} ) ) | + | sess.run( tf.mul( tf.nn.softmax( y ), target ), |
| − | + | feed_dict={ x: x_train_np, target : y_train_np} ) ) | |
| − | + | ||
| − | |||
| − | |||
# | # | ||
#prediction = tf.reduce_sum( tf.mul( tf.nn.softmax( y ), target ), reduction_indices=1 ) | #prediction = tf.reduce_sum( tf.mul( tf.nn.softmax( y ), target ), reduction_indices=1 ) | ||
accuracyNum = sess.run( accuracy, feed_dict={x: x_train_np, target : y_train_np} ) | accuracyNum = sess.run( accuracy, feed_dict={x: x_train_np, target : y_train_np} ) | ||
| − | print( "Final Accuracy on training data = %1.2f%%" % (100.0*accuracyNum) | + | print( "Final Accuracy on training data = %1.2f%%" % (100.0*accuracyNum) ) |
| − | ) | ||
accuracyNum = sess.run( accuracy, feed_dict={ x: x_test_np, target : y_test_np} ) | accuracyNum = sess.run( accuracy, feed_dict={ x: x_test_np, target : y_test_np} ) | ||
print( "Final Accuracy on test data = %1.2f%%" % (100.0*accuracyNum) ) | print( "Final Accuracy on test data = %1.2f%%" % (100.0*accuracyNum) ) | ||
</source> | </source> | ||
| − | + | <br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=Output= | =Output= | ||
<br /> | <br /> | ||
Latest revision as of 18:18, 27 March 2017
--D. Thiebaut (talk) 15:26, 19 March 2017 (EDT)
|
This page (which started as a Jupyter notebook) illustrates how to design a simple multi-layer Tensorflow Neural Net to recognize integers coded in binary and output them as a 1-hot vector. For example, if we assume that we have 5 bits, then there are 32 possible combinations. We associate with each 5-bit sequence a 1-hot vector. For example, 0,0,0,1,1, which is 3 in decimal, is associated with 0,0,0,1,0,0,0,0...,0, which has 31 0s and one 1. The only 1 is at Index 3. Similarly, if we have 1,1,1,1,1, which is 31 in decimal, then its associated 1-hot vector is 0,0,0,0,...0,0,1, another group of 31 0s and one last 1. Our binary input is coded in 5 bits, and we make it more interesting by adding 5 additional random bits. So the input is a vector of 10 bits, 5 random, and 5 representing a binary pattern associated with a 1-hot vector. The 1- hot vector is the output to be predicted by the network. |
Source Files
This tutorial is in the form of a Jupyter Notebook, and made available here in various forms:
- tgz-zipped archive containing the markdown and notebook
Preparing the Data
Let's prepare a set of data where we have 5 bits of input, plus 3 random bits, plus 32 outputs corresponding to
1-of for the integer coded in the 5 bits.
Preparing the Raw Data: 32 rows Binary and 1-Hot
We first create two arrays of 32 rows. The first array, called x32, contains the binary patterns for 0 to 31. The
second array, called y32, contains the one-hot version of the equivalent entry in the x32 array. For example,
[0,0,0,0,0] in x32 corresponds to [1,0,0,0,...,0] (one 1 followed by thirty one 0s) in y32. [1,1,1,1,1] in x32
corresponds to [0,0,0...,0,0,1] in y32.
from __future__ import print_function import random import numpy as np import tensorflow as tf # create the 32 binary values of 0 to 31 # as well as the 1-hot vector of 31 0s and one 1. x32 = [] y32 = [] for i in range( 32 ): n5 = ("00000" + "{0:b}".format(i))[-5:] bits = [0]*32 bits[i] = 1 #print( n5,":", r3, "=", bits ) nBits = [ int(n) for n in n5 ] #print( nBits, rBits, bits ) #print( type(x), type(y), type(nBits), type(rBits), type( bits )) x32 = x32 + [nBits] y32 = y32 + [bits] # print both collections to verify that we have the correct data. # The x vectors will be fed to the neural net (NN) (along with some nois y data), and # we'll train the NN to generate the correct 1-hot vector. print( "x = ", "\n".join( [str(k) for k in x32] ) ) print( "y = ", "\n".join( [str(k) for k in y32] ) )
Addition of Random Bits
Let's add some random bits (say 7) to the rows of x, and create a larger collection of rows, say 100.
x = [] y = [] noRandomBits = 5 for i in range( 100 ): # pick all the rows in a round-robin fashion. xrow = x32[i%32] yrow = y32[i%32] # generate a random int of 5 bits r5 = random.randint( 0, 31 ) r5 = ("0"*noRandomBits + "{0:b}".format(r5))[-noRandomBits:] # create a list of integer bits for r5 rBits = [ int(n) for n in r5 ] #create a new row of x and y values x.append( xrow + rBits ) y.append( yrow ) # display x and y for i in range( len( x ) ): print( "x[%2d] ="%i, ",".join( [str(k) for k in x[i] ] ), "y[%2d] ="%i, ",".join( [str(k) for k in y[i] ] ) )
Split Into Training and Testing
We'll split the 100 rows in 90 rows of training, and 10 rows for testing.
Percent = 0.10 x_train = [] y_train = [] x_test = [] y_test = [] # pick 10 indexes in 0-31. indexes = [5, 7, 10, 20, 21, 29, 3, 11, 12, 25] for i in range( len( x ) ): if i in indexes: x_test.append( x[i] ) y_test.append( y[i] ) else: x_train.append( x[i] ) y_train.append( y[i] ) # display train and set xs and ys for i in range( len( x_train ) ): print( "x_train[%2d] ="%i, ",".join( [str(k) for k in x_train[i] ] ), "y_train[%2d] ="%i, ",".join( [str(k) for k in y_train[i] ] ) ) print() for i in range( len( x_test ) ): print( "x_test[%2d] ="%i, ",".join( [str(k) for k in x_test[i] ] ), "y_test[%2d] ="%i, ",".join( [str(k) for k in y_test[i] ] ) )
Package Xs and Ys as Numpy Arrays
We now make the train and test arrays into numpy arrays.
x_train_np = np.matrix( x_train ).astype( dtype=np.float32 ) y_train_np = np.matrix( y_train ).astype( dtype=np.float32 ) x_test_np = np.matrix( x_test ).astype( dtype=np.float32 ) y_test_np = np.matrix( y_test ).astype( dtype=np.float32 ) # get training size, number of features, and number of labels, using # NN/ML vocabulary train_size, num_features = x_train_np.shape train_size, num_labels = y_train_np.shape # Get the number of epochs for training. test_size, num_eval_features = x_test_np.shape test_size, num_eval_labels = y_test_np.shape # Get the size of layer one. if True: print( "tain size = ", train_size ) print( "num features = ", num_features ) print( "num labels = ", num_labels ) print() print( "test size = ", test_size ) print( "num eval features = ", num_eval_features ) print( "num eval labels = ", num_eval_labels )
Definition of the Neural Network
Let's define the neural net. We assume it has just 1 layer.
Constants/Variables
We just have one, the learning rate with which the gradient optimizer will look for the optimal weights. It's a
factor used when following the gradient of the function y = W.x + b, in order to look for the minimum of the
difference between y and the target.
learning_Rate = 0.1
Place-Holders
It will have place holders for
- the X input
- the Y target. That's the vectors of Y values we generated above. The network will generate its own version of y, which we'll compare to the target. The closer the two are, the better.
- the drop-probability, which is defined as the "keep_probability", i.e. the probability a node from the neural net will be kept in the computation. A value of 1.0 indicates that all the nodes are used in the processing of data through the network.
x = tf.placeholder("float", shape=[None, num_features]) target = tf.placeholder("float", shape=[None, num_labels]) keep_prob = tf.placeholder(tf.float32)
Variables
The variables contain tensors that TensorFlow will manipulate. Typically the Wi and bi coefficients of each layer.
We'll assume just one later for right now, with num_features inputs (the width of the X vectors), and num_labels
outputs (the width of the Y vectors). We initialize W0 and b0 with random values taken from a normal
distribution.
W0 = tf.Variable( tf.random_normal( [num_features, num_labels ] ) ) b0 = tf.Variable( tf.random_normal( [num_labels] ) ) W1 = tf.Variable( tf.random_normal( [num_labels, num_labels * 2 ] ) ) b1 = tf.Variable( tf.random_normal( [num_labels * 2] ) ) W2 = tf.Variable( tf.random_normal( [num_labels * 2, num_labels ] ) ) b2 = tf.Variable( tf.random_normal( [num_labels] ) )
Model
The model simply defines what the output of the NN, y, is as a function of the input x. The softmax function
transforms the output into probabilities between 0 and 1. This is what we need since we want the output of our
network to match the 1-hot vector which is the format the y vectors are coded in.
#y0 = tf.nn.sigmoid( tf.matmul(x, W0) + b0 ) y0 = tf.nn.sigmoid( tf.matmul(x, W0) + b0 ) y1 = tf.nn.sigmoid( tf.matmul(y0, W1) + b1 ) y = tf.matmul( y1, W2) + b2 #y = tf.nn.softmax( tf.matmul( y0, W1) + b1 )
Training
We now define the cost operation, cost_op, i.e. measuring how "bad" the output of the network is compared to
the correct output.
#prediction = tf.reduce_sum( tf.mul( tf.nn.softmax( y ), target ), reduction_indices=1 ) #accuracy = tf.reduce_mean ( prediction ) #cost_op = tf.reduce_mean( tf.sub( 1.0, tf.reduce_sum( tf.mul( y, target ), reduction_indices=1 ) ) ) #cost_op = tf.reduce_mean( # tf.sub( 1.0, tf.reduce_sum( tf.mul( target, tf.nn.softmax(y) ), reduction_indices=[1] ) ) # ) # The cost_op below yields an ccuracy on training data of 0.86% and an a ccuracy on test data = 0.49% # for 1000 epochs and a batch size of 10. cost_op = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits( labels = target, logits = y ) )
And now the training operation, or train_op, which is given the cost_op
#train_op = tf.train.GradientDescentOptimizer( learning_rate = learning_Rate ).minimize( cost_op ) train_op = tf.train.AdagradOptimizer( learning_rate = learning_Rate ).minimize( cost_op )
Initialization Phase
We need to create an initialization operation, init_op, as well. It won't be executed yet, not until the session
starts, but we have to do it first.
init_op = tf.initialize_all_variables()
Start the Session
We are now ready to start a session!
sess = tf.Session() sess.run( init_op )
Training the NN
We now train the Neural Net for 1000 epoch. In each epoch we feed just one vector of x to the network.
batchSize = 5 prediction = tf.equal( tf.argmax( y, 1 ), tf.argmax( target, 1) ) accuracy = tf.reduce_mean ( tf.cast( prediction, tf.float32 ) ) for epoch in range( 10000 ): for i in range( 0, train_size, batchSize ): xx = x_train_np[ i:i+batchSize, : ] yy = y_train_np[ i:i+batchSize, : ] sess.run( train_op, feed_dict={x: xx, target: yy} ) if epoch%100 == 0: co, to = sess.run( [cost_op,train_op], feed_dict={x: x_train_np, target: y_train_np} ) print( epoch, "cost =", co, end=" " ) accuracyNum = sess.run( accuracy, feed_dict={x: x_train_np, target : y_train_np} ) print( "Accuracy on training data = %1.2f%%" % (accuracyNum*100), end = " " ) accuracyNum = sess.run( accuracy, feed_dict={ x: x_test_np, target : y_test_np} ) print( "Accuracy on test data = %1.2f%%" % ( accuracyNum*100 ) ) if False: print( "y = ", sess.run( y, feed_dict={ x: x_train_np, target : y_train_np} ) ) print( "softmax(y) = ", sess.run( tf.nn.softmax( y ), feed_dict={ x: x_train_np, target : y_train_np} ) ) print( "tf.mul(tf.nn.softmax(y), target) = ", sess.run( tf.mul( tf.nn.softmax( y ), target ), feed_dict={ x: x_train_np, target : y_train_np} ) ) # #prediction = tf.reduce_sum( tf.mul( tf.nn.softmax( y ), target ), reduction_indices=1 ) accuracyNum = sess.run( accuracy, feed_dict={x: x_train_np, target : y_train_np} ) print( "Final Accuracy on training data = %1.2f%%" % (100.0*accuracyNum) ) accuracyNum = sess.run( accuracy, feed_dict={ x: x_test_np, target : y_test_np} ) print( "Final Accuracy on test data = %1.2f%%" % (100.0*accuracyNum) )
Output
0 cost = 4.06461 Accuracy on training data = 7.78% Accuracy on test data = 0.00% 100 cost = 0.0568146 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 200 cost = 0.0249612 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 300 cost = 0.0156735 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 400 cost = 0.0113394 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 500 cost = 0.00885047 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 600 cost = 0.00724066 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 700 cost = 0.00611609 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 800 cost = 0.00528698 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 900 cost = 0.00465089 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1000 cost = 0.00414775 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1100 cost = 0.00374 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1200 cost = 0.00340309 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1300 cost = 0.00312006 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1400 cost = 0.00287907 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1500 cost = 0.00267149 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1600 cost = 0.00249079 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1700 cost = 0.00233219 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1800 cost = 0.00219193 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 1900 cost = 0.00206695 Accuracy on training data = 100.00% Accuracy on test data = 90.00% 2000 cost = 0.00195495 Accuracy on training data = 100.00% Accuracy on test data = 90.00%