Difference between revisions of "CSC270 Lab 2 2011"
(→Experiment #2) |
(→Experiment #1: Python to the rescue) |
||
| Line 10: | Line 10: | ||
==Experiment #1: Python to the rescue== | ==Experiment #1: Python to the rescue== | ||
| − | For this experiment, you | + | For this experiment, you will use one of the lab laptops, boot it with Ubuntu (DVD provided), and write a Python program. |
| − | The program below | + | The program below, written in Python, generates the truth table of two functions f(a,b,c) and g(a,b,c) of three input variables. f is defined as <tt>((not a) and b ) or c</tt> and g is defined as <tt>( not a) and (not b) and (not c)</tt>. |
<code><pre> | <code><pre> | ||
| Line 61: | Line 61: | ||
</pre></code> | </pre></code> | ||
| − | + | :Experiment #1 | |
| + | ; Create and run the program above. verify that you get the same truth table as shown here. (You may want to mail the code and output to yourself to simplify the taks of writing your report later on.) | ||
| − | + | :Experiment #2 | |
| + | ; Modify your program and make it output the truth table for a 2-bit binary adder. | ||
| + | |||
| + | |||
| + | =Experiment #2= | ||
| + | |||
| + | * Implement the 2-bit adder with AND, OR, NOT and possibly XOR gates (the XOR is packaged in a 74LS86 circuit). | ||
| + | |||
| + | * Demonstrate that your circuit works! | ||
| + | |||
| + | |||
| + | =Experiment #3= | ||
| + | |||
| + | * Implement a 3-bit adder with similar gates. | ||
| + | |||
| + | =Experiment #4 (depending on time available)= | ||
| + | |||
| + | * Implement the 2-bit adder with NAND gates only. | ||
| + | |||
| + | |||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | [[Category:CSC270]][[Category:Labs]] | ||
==Experiment #2== | ==Experiment #2== | ||
Revision as of 22:16, 30 January 2011
Back to the weekly schedule
Contents
LAB #2
© D. Thiebaut, 2009
Experiment #1: Python to the rescue
For this experiment, you will use one of the lab laptops, boot it with Ubuntu (DVD provided), and write a Python program.
The program below, written in Python, generates the truth table of two functions f(a,b,c) and g(a,b,c) of three input variables. f is defined as ((not a) and b ) or c and g is defined as ( not a) and (not b) and (not c).
# truthtable.py
# D. Thiebaut
# how a simple python program can generate the
# truth table of a boolean function
#
# here f is a function of 3 variables
# _
# f = a.b + c
# _ _ _
# g = a + b + c
def f( a, b, c ):
return ( a & (not b) ) | c
def g( a, b, c ):
return (not a) | (not b) | (not c)
def main():
print " a b c | f g "
print "-----------+--------"
for a in [ 0, 1 ]:
for b in [ 0, 1 ]:
for c in [ 0, 1 ]:
print "%3d%3d%3d |%3d%3d" % \
( a, b, c, f( a, b, c ), g( a, b, c ) )
main()
The output is show below:
a b c | f g
-----------+--------
0 0 0 | 0 1
0 0 1 | 1 1
0 1 0 | 0 1
0 1 1 | 1 1
1 0 0 | 1 1
1 0 1 | 1 1
1 1 0 | 0 1
1 1 1 | 1 0
- Experiment #1
- Create and run the program above. verify that you get the same truth table as shown here. (You may want to mail the code and output to yourself to simplify the taks of writing your report later on.)
- Experiment #2
- Modify your program and make it output the truth table for a 2-bit binary adder.
Experiment #2
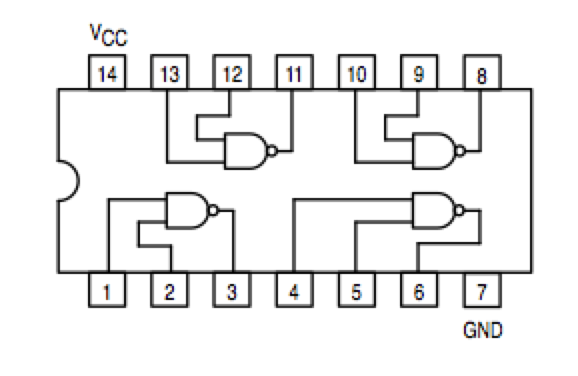
- Implement the 2-bit adder with AND, OR, NOT and possibly XOR gates (the XOR is packaged in a 74LS86 circuit).
- Demonstrate that your circuit works!
Experiment #3
- Implement a 3-bit adder with similar gates.
Experiment #4 (depending on time available)
- Implement the 2-bit adder with NAND gates only.
Experiment #2
Implement the Id0 and Id1 signals of the majority voter with the simplest circuit you can come up with. Demonstrate that it works and returns the Id of the faulty input, except when the three inputs are the same, in which case the two signals are 1 1.
Experiment #3
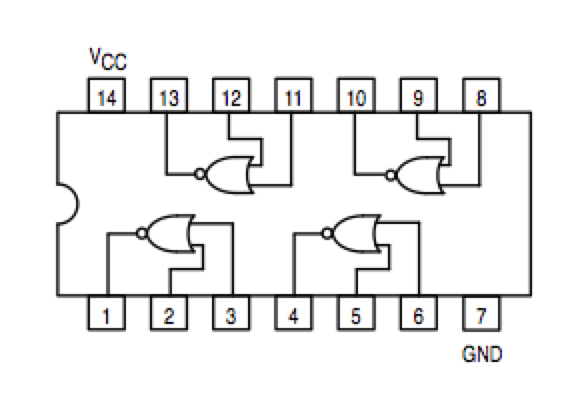
Same as Experiment #2, but use only NAND gates for one of the signals, and only NOR gates for the other.
|
|
Note that the NOR circuit does not have the same pinout as the NAND circuit!!!