Difference between revisions of "CSC270 Midterm Prep 2012"
| Line 13: | Line 13: | ||
* Implement f above with NANDs only. With NORs only. | * Implement f above with NANDs only. With NORs only. | ||
<br /> | <br /> | ||
| + | <br /> | ||
| + | * Assume that you have a desk with 3 drawers and a secret compartment. The drawers have electronic sensors that detect if a drawer is open (1) or closed (0). We want to build a simple circuit that will activate a release signal (set it to 1) to open the secret compartment only if the right combination of steps is taken. | ||
| + | :This combination of steps is: | ||
| + | :# All drawers are closed | ||
| + | :# Drawer 1 is open | ||
| + | :# Drawer 1 is closed | ||
| + | :# Drawer 3 is open and stays open | ||
| + | :# Drawer 2 is open | ||
| + | :# Drawer 2 is closed | ||
| + | |||
| + | :At this point the release signal is activated. It stays on as long as none of the drawers move. The secret compartment opens! | ||
| + | |||
| + | ;Question | ||
| + | :How many states to you need? | ||
| + | <br /> | ||
* Implement the function below with a 4-to-16 decoder. The decoder has active-low outputs and an active-low enable. Be efficient in your design. | * Implement the function below with a 4-to-16 decoder. The decoder has active-low outputs and an active-low enable. Be efficient in your design. | ||
Revision as of 09:33, 9 March 2012
--D. Thiebaut 08:40, 9 March 2012 (EST)
Below are some problems that will help you prepare for the midterm.
- Assume you have a boolean function f defined as:
- f = Σ(1,3,5).
- Give the maxterm canonical form of f.
- Implement f above with NANDs only. With NORs only.
- Assume that you have a desk with 3 drawers and a secret compartment. The drawers have electronic sensors that detect if a drawer is open (1) or closed (0). We want to build a simple circuit that will activate a release signal (set it to 1) to open the secret compartment only if the right combination of steps is taken.
- This combination of steps is:
- All drawers are closed
- Drawer 1 is open
- Drawer 1 is closed
- Drawer 3 is open and stays open
- Drawer 2 is open
- Drawer 2 is closed
- At this point the release signal is activated. It stays on as long as none of the drawers move. The secret compartment opens!
- Question
- How many states to you need?
- Implement the function below with a 4-to-16 decoder. The decoder has active-low outputs and an active-low enable. Be efficient in your design.
- f = Σ(0,1,3,4,5,6,7,8,9,10,11,12,14)
- Implement a 3-to-8 decoder with several 2-to-4 decoders. You may assume that the decoders have
enable inputs, and you are free to choose active-high or active-low signals.
- What is the boolean representation of the function f shown in the figure below? Express f in its
simplest form.
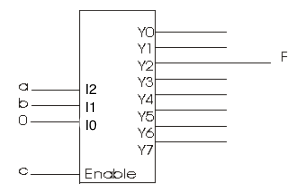
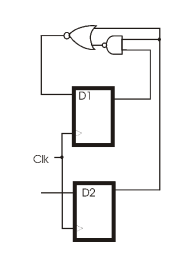
- What is the state diagram of the sequential circuit shown below, if D2 is set to 1 always? If D2 is set to
0 always?
- Assume that you have a desk with 3 drawers and a secret compartment. The drawers have electronic sensors that detect if a drawer is open (1) or closed (0). We want to build a simple circuit that will activate a release signal (set it to 1) to open the secret compartment only if the right combination of steps is taken.
- This combination of steps is:
- All drawers are closed
- Drawer 1 is open
- Drawer 1 is closed
- Drawer 3 is open and stays open
- Drawer 2 is open
- Drawer 2 is closed
- At this point the release signal is activated. It stays on as long as none of the drawers move. The secret compartment opens!
- Question
- How many states to you need?
- We want to implement a GYR sequencer where Green stays on for approximately 1 minute, Yellow for approximately 15 seconds, and Red for approximately 45 seconds. You have available to you a clock generator that generates a 1Hz, 1KHz, and 100KHz signal.
- Figure out a way to generate a simple design with as few states as possible.
- How many flip-flops will you need?