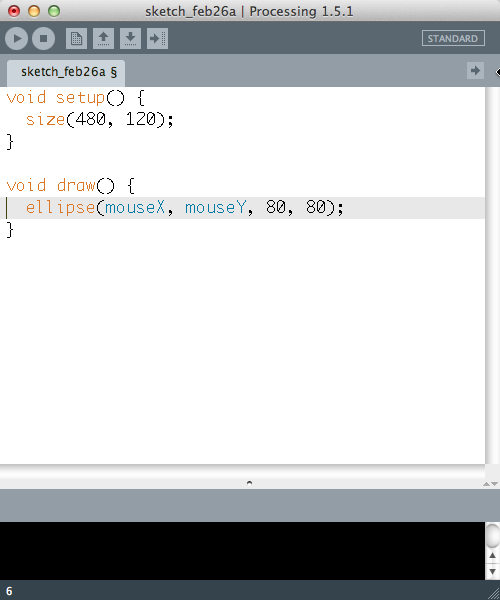
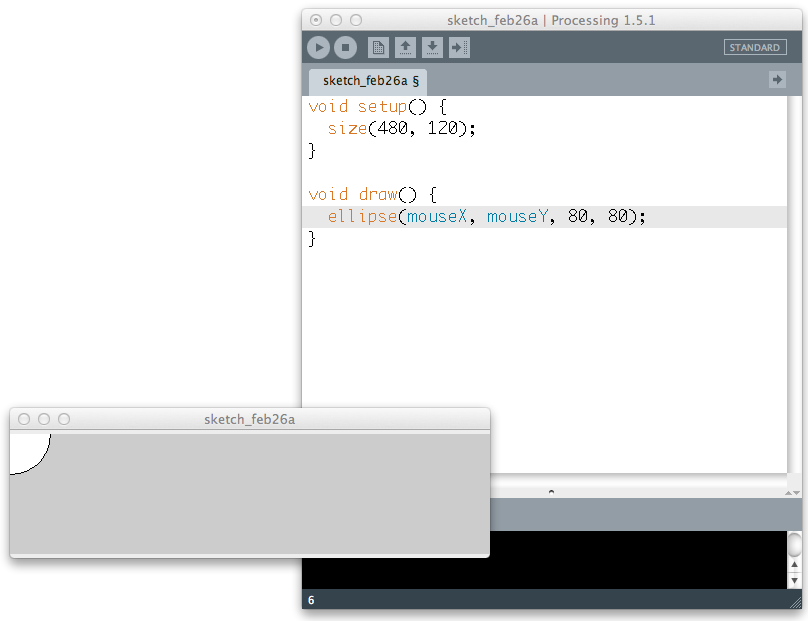
Difference between revisions of "CSC103: DT's Notes 1"
(→Current Computer Design is the Result of an Evolutionary Process) |
(→Current Computer Design is the Result of an Evolutionary Process) |
||
| Line 30: | Line 30: | ||
One can argue that if von Neumann hadn't written this report, we may have followed somebody else's brilliant idea for putting together a machine working with electricity, where information is stored and operated on in binary form. Our laptop today could be using a different architecture, and programming them might be a totally different type of problem solving. | One can argue that if von Neumann hadn't written this report, we may have followed somebody else's brilliant idea for putting together a machine working with electricity, where information is stored and operated on in binary form. Our laptop today could be using a different architecture, and programming them might be a totally different type of problem solving. | ||
| − | [[File:AntikytheraMecanism.png|right|frame|400px| Antikythera Mechanism, photo taken by Tilemahos Efthimiadis, National Archaeological Museum, Athens, Greece., taken from commons.wikimedia.org, July 28 2014. Released under the Creative Commons Attribution 2.0 Generic license.]] For computers were not always electrical machines. Initially they were mechanical machines. The abacus, which appeared several millennia B.C. was a counting machine made of wood. The [http://en.wikipedia.org/wiki/Antikythera_mechanism Antikythera] mechanism, is currently regarded as the first mechanical machine for computing astronomical calculations. Mechanical as well, the important machine in the history of computers is '''[http://en.wikipedia.org/wiki/Difference_engine Babbage's Difference Engine]'''. This one was made of gears and shafts, with a crank at the top, and was a ''general purpose'' machine. Interestingly, this machine has given us an expression we still use with modern electronic computers: we still hear programmers refer to "cranking out" the results, even though the crank is long gone. | + | [[File:AntikytheraMecanism.png|right|frame|thumb|400px| Antikythera Mechanism, photo taken by Tilemahos Efthimiadis, National Archaeological Museum, Athens, Greece., taken from commons.wikimedia.org, July 28 2014. Released under the Creative Commons Attribution 2.0 Generic license.]] For computers were not always electrical machines. Initially they were mechanical machines. The abacus, which appeared several millennia B.C. was a counting machine made of wood. The [http://en.wikipedia.org/wiki/Antikythera_mechanism Antikythera] mechanism, is currently regarded as the first mechanical machine for computing astronomical calculations. Mechanical as well, the important machine in the history of computers is '''[http://en.wikipedia.org/wiki/Difference_engine Babbage's Difference Engine]'''. This one was made of gears and shafts, with a crank at the top, and was a ''general purpose'' machine. Interestingly, this machine has given us an expression we still use with modern electronic computers: we still hear programmers refer to "cranking out" the results, even though the crank is long gone. |
The same is true of '''silicon transistors''' powered by electricity. Silicon is the material of choice for electronic microprocessor circuits as well as semiconductor circuits we find in today's computers. Its appeal lies in its property of being able to either conduct and not conduct electricity, depending on a signal it receives which is also electrical. Silicon allows us to create electrical switches that are very fast, very small, and consume very little power. But because we are very good at creating semiconductor | The same is true of '''silicon transistors''' powered by electricity. Silicon is the material of choice for electronic microprocessor circuits as well as semiconductor circuits we find in today's computers. Its appeal lies in its property of being able to either conduct and not conduct electricity, depending on a signal it receives which is also electrical. Silicon allows us to create electrical switches that are very fast, very small, and consume very little power. But because we are very good at creating semiconductor | ||
Revision as of 10:35, 6 August 2014
--© D. Thiebaut 2012, 2013, 2014
Last revised --D. Thiebaut (talk) 08:05, 9 October 2013 (EDT)
Contents
- 1 CSC103 How Computers Work--Class Notes
- 2 Logic Gates
- 3 Computer Simulator
- 3.1 Time to Play A Game
- 3.2 Computer Memory
- 3.3 The Processor
- 3.4 The Cookie Monster Analogy
- 3.5 Instructions and Assembly Language
- 3.6 A First Program
- 3.7 Summary/Points to Remember
- 3.8 The Von Neumann Bottleneck
- 3.9 Moore's Law
- 3.10 Introduction to the Language Processing
- 3.11 References
CSC103 How Computers Work--Class Notes
Introduction |
Current Computer Design is the Result of an Evolutionary Process |

In this course we are going to look at the computer as a tool, as the result of technological experiments that have crystalized currently on a particular design, the von Neumann architecture, on a particular source of energy, electricity, on a particular fabrication technology, silicon transistors, and a particular information representation, the binary system, but any of these could have been different, depending on many factors. In fact, in the next ten or twenty years, one of more of these fundamental parts that make today's computers could change.
Steamboy, a Japanese animé by director Katsuhiro Ohtomo (who also directed Akira) is interesting in more than the story of a little boy who is searching for his father, a scientist who has discovered a secret method for controlling high pressured steam. What is interesting is that the movie is science fiction taking place not in the future, but in middle of the 19th century, in a world where steam progress and steam machines are much more advanced than they actually were at that time. One can imagine that some events, and some discoveries where made in the world portrayed in the animated film, and that technology evolved in quite a different direction, bringing with it new machines, either steam-controlled tank-like vehicles, or ships, or flying machines.
For computers, we can make the same observation. The reason our laptops today are designed the way they are is really the result of happy accidents in some ways. The way computers are designed, for example, with one processor (more on multi-core processors later), a system of busses, and memory where both data and programs reside side-by-side hasn't changed since John von Neumann wrote his (incomplete and never officially published) First Draft of a Report on the EDVAC,[1] article, in June of 1945. One can argue that if von Neumann hadn't written this report, we may have followed somebody else's brilliant idea for putting together a machine working with electricity, where information is stored and operated on in binary form. Our laptop today could be using a different architecture, and programming them might be a totally different type of problem solving.
The same is true of silicon transistors powered by electricity. Silicon is the material of choice for electronic microprocessor circuits as well as semiconductor circuits we find in today's computers. Its appeal lies in its property of being able to either conduct and not conduct electricity, depending on a signal it receives which is also electrical. Silicon allows us to create electrical switches that are very fast, very small, and consume very little power. But because we are very good at creating semiconductor in silicon, it doesn't mean that it is the substrate of choice. Researchers have shown[2] that complex computation could also be done using DNA, in vials. Think about it: no electricity there; just many vials with solutions containing DNA molecules, a huge number of them, that are induced to code all possible combinations of a particular sequence, such that one of the combinations is the solution to the problem to solve. DNA computing is a form of parallel computation where many different solutions are computed at the same time, in parallel, using DNA molecules[3]. One last example for computation that is not performed in silicon by traveling electrons can be found in optical computing. The idea behind this concept (we really do not have optical computers yet, just isolated experiments showing its potential) is that electrons are replaced with photons, and these photons, which are faster than electrons, but much harder to control.
So, in summary, we start seeing that computing, at least the medium chosen for where the computation takes place can be varied, and does not have to be silicon. Indeed, there exist many examples of computational devices that do not use electronics in silicon and can perform quite complex computation. In consequence, we should also be ready to imagine that new computers in ten, twenty or thirty years will not use semiconductors made of silicon, and may not use electrons to carry information that is controlled by transistors. In fact, it is highly probable that they won't [1].
While the technology used in creating today's computer is the result of an evolution and choices driven by economic factors and scientific discoveries, among others, one thing we can be sure of is that whatever computing machine we devise and use to perform calculations, that machine will have to use rules of mathematics. It does not matter what technology we use to compute 2 + 2. The computer must follow strict rules and implement basic mathematical rules in the way it treats information.
You may think that Math may be necessary only for programs that, say, display a mathematical curve on the screen, or maintain a spreadsheet of numbers representing somebody's income tax return, but Math might probably not be involved in a video game where we control an avatar who moves in a virtual world. Or that the computer inside a modern data phone is probably not using laws of Mathematics for the great majority of what we du with it during the day. This couldn't be further from the truth. Figuring out where a tree should appear on the screen as our avatar is moving in its virtual space requires applying basic geometry in three dimensions: the tree is at a corner of a triangle formed by the tree, the avatar, and the eye of the virtual camera showing you the image of this virtual world. Our phone's ability to pin point its location as we're sitting in a café sipping on a coffee, requires geometry again, a program deep in the phone figuring out how far we are from various signal towers for which the phone knows the exact location, and using triangulation techniques to find our place in relationship to them.
So computers, because they need to perform mathematical operations constantly, must know the rules of mathematics. Whatever they do, they must do it in a way that maintains mathematical integrity. They must also be consistent and predictable. 2 + 2 computed today should yield the same result tomorrow, independent of which computer we use. This is one reason we send mathematical equations onboard space probes that are sent to explore the universe outside our solar system. If there is intelligent life out there, and if it finds our probe, and if it looks inside, it will find math. And the math for this intelligent life will behave the same as math for us. Mathematics, its formulas, its rules, are universal.
But technological processes are not. So computers can be designed using very different technologies, but whatever form they take, they will follow the rules of math when performing computations.
In our present case, the major influence on the way our computers are build is the fact that we are using electricity as the source of power, and that we're using fast moving electrons to represent, or code information. Electrons are cheap. They are also very fast, moving at approximately 3/4 the speed of light in wires[4]. We know how to generate them cheaply (power source), how to control them easily (with switches), and how to transfer them (over electrical wires). These properties were the reason for the development of the first vacuum tube computer by Atanasoff in 1939[5].
The choice of using electricity has influenced greatly a fundamental way in which modern computers work. They all use the binary system at the lowest level. Because electricity can be turned ON or OFF with a switch, it was only logical that these two states would be used to represent information. ON and OFF. 0 and 1. True and False. But if we can represent two different states, two different levels of information, can we represent other than 0 or 1? Say 257? Can we also organize electrical circuitry that can perform the addition of two numbers? The answer is Yes; using the binary numbering system.
Binary System |
This section is an overview of the binary system. Better sources of information can be found on this subject, including this one from the University of Vermont.
To better understand the binary system, we'll refresh our memory about the way our decimal system works, figure out what rules we use to operate in decimal, and carry them over to binary.
First, we'll need to define a new term. The base of a system is the number of digits used in the system. Decimal: base 10: we have 10 digits to write numbers with: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
In binary, the base is 2; we have only two digits to write numbers with: 0, and 1.
Counting in Decimal |
Let's now count in decimal and go slowly, figuring out how we come up with the numbers.
000
That's the first positive number. Instead of just 1 zero, we pad the number with leading zeros so that the number has 3 digits. This will help us understand better the rule we're so good at using that we have forgotten it!
Let's continue:
001 002 003 004 005 006 007 008 009 ----------
Ok, now an important point in the counting process. We have written all 10 digits in the right-most position of our number. Because we could increment this digit, we didn't have to change the digits on the left. Now that we have reached 9, we need to roll over the list of digits. We have to go from 9 back to 0. Because of this roll-over, we have to increment (that means adding 1) the digit that is directly to the left of the one rolling over.
0 0 9 ! | the |-symbol shows 9 rolling over to 0 ! | the !-symbol shows that as 9 rolls over, its left neighbor gets incremented by 1 0 1 0
Let's continue:
010 011 ... 019 ---------- 020 021 022 ... 029 ---------- 030 ... 098 099 ---------- 100 101 ...
Notice that after a while we reach 019. The right-most digit has to roll over again, which makes it become 0, and the digit to its left must be incremented by 1. From 1 it becomes 2, and we get 020.
At some point, applying this rule we reach 099. Let's just apply our simple rule: the right most digit must roll over, so it becomes 0, and the digit to its left increments by 1. Because this second digit is also 9 it, too, must roll over and become 0. And because the 2nd digit rolls over, then the third digit increments by 1. We get 100. Does that make sense? We are so good at doing this by heart without thinking of the process we use that sometimes it is confusing to deconstruct such knowledge.
So let's remember this simple rule; it applies to counting in all number systems, whether they are in base 10 or some other base:
Counting in Binary |
Let's now count in base 2, in binary. This time our "internal" table contains only 2 digits: 0, 1. So, whatever we do, we can only use 0 and 1 to write numbers. And the list of numbers we use and from which we'll "roll-over" is simply: 0, 1.
00000
Good start! That's zero. It doesn't matter that we used 5 0s to write it. Leading 0s do not change the value of numbers, in any base whatsoever. We use them here because they help see the process better.
We apply the rule: modify the right-most digit and increment it. 0 becomes 1. No rolling over.
00001
Good again! One more time: we increment the rightmost digit, but because we have reached the end of the available digits, we must roll over. The right-most digit becomes 0, and we increment its left neighbor:
00010
Once more: increment the right-most digit: this time it doesn't roll-over, and we do not modify anything else.
00011
One more time: increment the right-most digit: it rolls over and becomes 0. We have to increment its neighbor to the left, which also rolls over and becomes 0, and forces us to increment its neighbor to the left, the middle digit, which becomes 1:
00100
Let's pick up the pace:
00101 00110 00111 01000 ...
And so on. That's basically it for counting in binary.
Let's put the numbers we've generated in decimal and in binary next to each other:
decimal binary 000 00000 001 00001 002 00010 003 00011 004 00100 005 00101 006 00110 007 00111 008 01000 009 01001 010 01010 ...
- Exercise
- How would we count in base 3? The answer is that we just need to modify our table of available digits to be 0, 1, 2, and apply the rule we developed above. Here is a start:
0000 0001 0002 0010 (2 rolls over to 0, therefore we increment its left neighbor by 1) ...
- Does that make sense? Continue and write all the numbers until you reach 1000, in base 3.
Evaluating Binary Numbers |
What is the decimal equivalent of the binary number 11001 in decimal? To find out, we return to the decimal system and see how we evaluate, or find the value represented by a decimal number. For example:
1247
represents one thousand two hundred forty seven, and we are very good at imagining how large a quantity that is. For example, if you were told that you were to carry 1247 pennies in a bag, you get a sense of how heavy that bag would be.
The value of 1247 is 1 x 1000 + 2 * 100 + 4 * 10 + 7 * 1. The 1000, 100, 10, and 1 factors represent different powers of the base, 10. We can also rewrite it as
1247 = 1 x 103 + 2 x 102 + 4 x 101 + 7 x 100 = 1 x 1000 + 2 x 100 + 4 x 10 + 7 x 1 = 1247
So the rule here is that to find the value or weight of a number written in a particular base is to multiply each digit by the base raised to increasing powers, starting with the power 0 for the rightmost digit.
Let's try that for the binary number 11001. The base is 2 in this case, so the value is computed as:
11001 = 1 x 24 + 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 1 x 16 + 1 x 8 + 0 x 4 + 0 x 2 + 1 x 1 = 16 + 8 + 0 + 0 + 1 = 25 in decimal
Binary Arithmetic |
So far, we can count in binary, and we now how to find the decimal value of a binary number. But could we perform arithmetic with binary numbers? If we can, then we're that much closer to figure out how to build a computer that can perform computation. Remember, that's our objective in this chapter: try to understand how something build with electronic circuits that operate with electricity that can be turned on or off can be used to perform the addition of numbers. If we can add numbers, surely we can also multiply, subtract, divide, and we have an electronic calculator.
Once again we start with decimal. Base 10. Only 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Let's add 133 to 385
1 3 3 + 3 8 5 ------------
It's tempting to just go ahead and find the answer, isn't it? Instead let's do it a different way and concentrate only on 3 + 5. For this we write down the list of all available digits, in increasing order of weights. For the purpose of this section, we'll call this list of digits the table of available digits.
0 1 2 3 <---- we start at 3 4 +1 5 +2 6 +3 7 +4 8 +5 and we go down by 5 steps. 9
The result is 8.
1 3 3 + 3 8 5 ------------ 8
We move on the next column and add 3 + 8. Using our table of digits, this is what we get:
0 1 2 3 <---- we start at 3 4 +1 5 +2 6 +3 7 +4 8 +5 9 +6 ----- 1 0 +7 1 1 +8 <--- the result is 8, but with a roll-over
Here we had to roll over our list of available digits. We know the rule! When we roll over we add 1 to the digit on the left. In this case the digits on the left. We'll put this new digit (red) above the third column of numbers as follows:
1 1 3 3 + 3 8 5 ------------ 1 8
So now we have 3 numbers to add: 1, 1 and 3:
0 1 <---- we start at 1 2 +1 3 +and we start again adding 3: +1 4 +2 5 +3 6 7 8 9
The result:
1 3 3 + 3 8 5 ------------ <font color="magenta">5</font> 1 8
If we find ourselves in the case where adding the leftmost digits creates a roll-over, we simply pad the numbers with 0 and we find the logic answer.
So we have a new rule to add numbers in decimal, but actually one that should hold with any base system:
We align the numbers one above the other. We start with rightmost column of digits. We take the first digit in the column and start with it in the table of digits. We then go down the table a number of steps equivalent to the digit we have to add to that number. Which ever digit we end up on in the table that's the digit we put down as the answer. If we have to roll-over when we go down the table, then we put a 1 in the column to the left. We then apply the rule to the next column of digits to the left, until we have processed all the columns.
Ready to try this in binary? Let's take two binary numbers and add them:
1010011 + 0010110 ------------
Our table of digits is now simpler:
0
1
Here we start with the leftmost column, start at 1 in the table and go down by 0. The result is 1. We don't move in the table:
1010011 + 0010110 ------------ 1
Done with the rightmost column. We move to the next column and add 1 to 1 (don't think too fast and assume it's 2! 2 does not exist in our table of digits!)
0 1 <---- we start here, and go down by 1 ------ <font color="red">1</font> <font color="magenta">0</font> +1
We had to roll-over in the table. Therefore we take a carry of 1 and add it to the column on the left.
<font color="red">1</font> 1010011 + 0010110 ------------ <font color="magenta">0</font>1
Continuing this we finally get
1 1010011 + 0010110 ------------ 1101001
Let's verify that this is the correct answer. 1010011, in decimal is 64 + 16 + 2 + 1 = 83. 10110 is 16 + 4 + 2 = 22. 83 + 22 is 105. There 1101001 must represent 105. Double check: 1101001 is 64 + 32 + 8+ 1 which, indeed is 105.
So, in summary, it doesn't matter if we are limited to having only two digits, we can still count, represent numbers, and do arithmetic.
Summary of Where we Are |
Let's summarize what we know and what we're after. We know that electricity is cheap, easy to control, a great source of power, and that we can easily build switches that can control voltages over wire. We know that we can create a code associating 1 to electricity being ON and 0 to electricity being OFF in a wire. So electricity can be used to represent the numbers 0 and 1.
Furthermore, we know that a system where we only have two digits is called the binary system, and that this system is mathematically complete, allowing us to do everything we can do in decimal (we have concentrated in the previous discussion to just counting and adding, but we can do everything else the same).
So the question now for engineers around the middle of the 20th century was how to build electrical/electronic circuits that would perform arithmetic.
The answer to this problem is provided by two giants of computer science, George Boole , and Claude Shannon who lived at very different times, but provided two complementary parts of the solution. Boole (1815-1864) defined the Boolean algebra, a logic system that borrowed from philosophy and from mathematics, where assertions (mathematicians say variables) can only be true' or false, and where assertions can be combined by any combination of three conjunctions (which mathematicians call operators): and, or and not.
Many years later, Claude Shannon (1916-2001) showed in his Master's thesis that arithmetic operations on binary numbers could be performed using Boole's logic operators. In essence, if we map True and False to 1 and 0, adding two binary numbers can be done using logic operations.
We'll now look at Boole and Shannon separately.
Boole and the Boolean Algebra |
Boole's contribution is a major one in the history of computers. In the 1840s, he conceived of a mathematical world where there would be only two symbols, two values, and three operations that could be performed with them, and he proved that such a system could exhibit the same rules exhibited by an algebra. The two values used by Boole's algebra are True and False, or T and F, and the operators are and, or and not. Boole was in fact interested in logic, and expressing combinations of statements that can either be true or false, and figuring out whether mathematics could be helpful in formulating a logic system where we could express any logical expression containing multiple simple statements that could be either true or false.
While this seems something more interesting to philosophers than mathematicians or engineers, this system is the foundation of modern electronic computers.
Each of the boolean operators can be expressed by a truth table.
| a | b | a and b |
|---|---|---|
|
F |
F |
F |
|
F |
T |
F |
|
T |
F |
F |
|
T |
T |
T |
The table above is the truth table for the and logical operator. It says that if the statement a is true, and if b is false, then the and operator makes the result of a and b false. Only if both statements are true will the result of and-ing them together be true. This is still pretty abstract. Let's see if we can make this clearer. Assume that a is the statement Today is Monday, and that b is the statement The time is 9:00 a.m., and that you want to be reminded every Monday at 9:00 a.m. to go to Ford Hall to take a particular class. So we can define the alarm signal that reminds you to be a and b. The alarm will ring only when the day is Monday, and the time is 9:00 a.m. At 9:00 a.m. on Tuesdays nothing will happen, because at that particular time a is false, and b is true, but the and operator is extremely strick and will not generate true if only one of its operands is true.
The truth table for the or operator is the following:
| a | b | a or b |
|---|---|---|
|
F |
F |
F |
|
F |
T |
T |
|
T |
F |
T |
|
T |
T |
T |
Let's keep our alarm example and think of how to program an alarm so that we can spend the morning in bed and not get up early on Saturdays and Sundays. We could have Statement a be "Today is Saturday", and Statement b be "Today is Sunday". The boolean expression that will allow us to enjoy a morning in bed on weekends is a or b. We can make our decision by saying: "if a or b, we can stay in bed." On Saturdays, a is true, and the whole expression is true. On Sundays, b is true, and we can also stay in bed. On any other day, both a and b are false, and or-ing them together yields false, and we'd better get up early!
This all should start sounding familiar and "logical" by now. In fact, we use the same logic when searching for information on the Web, or at the library. For example, assume we are interested in searching for information about how to write a class construct in the language Python. You could try to enter Python class, which most search engine will internally translate as a search for "Python and class". Very likely you might find that the results include references to python the animal, not the programming language. So to prevent this from happening we can specify our search as python and class and (not snake).
Back to the alarm example. Assume that we have the same a and b boolean variables as previously, one that is true on Saturdays only and one that is true on Sundays only. How could we make this alarm go off for any weekday and not on weekends? We could simply say that we want the opposite of the alarm we had to see if we can stay in bed on weekends. So that would be not ( a or b ).
For completeness we should show the truth table for the not operator. It's pretty straightforward, and shown below:
| a | not a |
|---|---|
|
F |
T |
|
T |
F |
When a is true, not a is false, and conversely.
- An Example and Exercise
- Assume we want to build a logical machine that can use the logical operators and, or and not to help us buy ice cream for a friend. The friend in question has very specific taste, and likes ice cream with chocolate in it, ice cream with fruit in it, but not Haagen Dazs ice cream. This example and exercise demonstrate how we can build such a "machine".
We can devise three boolean variables that can be true of false depending on three properties of a container of ice cream: choc, fruit, and HG. choc is true if the ice cream contains some chocolate. fruit is true if the ice cream contains fruits, and HG is true if the ice cream is from Haagen Dazs. A boolean function, or expression, we're going to call it isgood, containing choc, fruit, and HG that turns true whenever the ice cream is one our friend will like would be this:
isgood = ( choc or fruit ) and ( not HG )
Any ice cream container for which choc or fruit is true, and which is not HG will match our friend's taste.
We could represent this boolean function with a truth table as well.
| choc | fruit | HG | choc or fruit | not HG | ( choc or fruit ) and ( not HG ) |
|---|---|---|---|---|---|
| F | F | F | F | T | F |
| F | F | T | F | F | F |
| F | T | F | T | T | T |
| F | T | T | T | F | F |
| T | F | F | T | T | T |
| T | F | T | T | F | F |
| T | T | F | T | T | T |
| T | T | T | T | F | F |
The important parts of the table above are the first 3 columns and the last one. The first 3 columns list all the possibilities of having three boolean variables take all possible values of true and false. That corresponds to 2 x 2 x 2 = 8 rows. Let's take Row 4. It corresponds to the case choc = false, fruit = true, and HG = true. The fourth column shows the result of or-ing choc and fruit. Looking at the truth table for or above, we see that the result of false with true is true. Hence the T on the fourth row, fourth column. Column 5 contains not HG. Since HG is true on Row 4, then not HG is false. The sixth column represent the and of Column 4 with Column 5. If we and true and false, the truth table for and says the result is false. Hence that particular ice cream would not be good for our friend. That makes sense, our friend said no ice cream from Haagen Dazs, and the one with just picked does.
Below are some questions for you to figure out:
- Question 1
- Which row of the table would correspond to a container of Ben and Jerry's vanilla ice cream? Would our friend like it?
- Question 2
- How about a container of Ben and Jerry's strawberry chocolate ice cream?
- Question 3
- Assume that our friend has a younger brother with a different boolean equation for ice cream. His equation is ( (not choc) and fruit) and ( HG or ( not HG ) ). Give an example of several ice cream flavors and makers of ice cream the young brother will like.
- Question 4 (challenging)
- Can you find an ice cream flavor and maker that both our friend and his/her younger brother will like?
Shannon's MIT Master's Thesis: the missing link |
We are now coming to Shannon, who's influence on the field of computer science is quite remarkable, and whose contribution of possibly greatest influence was his Master's thesis at MIT, written in 1948.
Shannon knew of the need for calculators (human beings or machines) around the time of the second world-war, (the need was particularly great for machines that would compute tables of possible trajectories for shells fired from canons). He also knew of efforts by various groups in universities to build calculating machines using electricity and relays, and also of early experiments with vacuum tubes (which later replaced the relays). Because the machines used electricity and switches, the binary system with only two values, 0 and 1 was an appealing system to consider and exploit. But there was still an engineering gap in figuring out how to create circuits that would perform arithmetic operations on binary numbers in an efficient way.
Also known at the time was the fact that Boolean logic was easy to implement with electrical systems. For example, creating a code system where a switch can represent the values of True or False is easy, as illustrated in the figure below, in the first (1) panel.
The black lines represent electrical wires carrying an electrical current. The two circles with an oblique bar represent an electrical switch, that can be ON or OFF. In the figure it is represented in the OFF position. In this position, no current can flow. When the
oblique bar, which is a metalic object is brought down to touch the second white circle, it makes contact with the wire on the right, and the current can flow through the switch. In this case we can say that the OFF position of the switch represents the value False, and the ON position of the switch represents the value True, and the switch represents a boolean variable. If it is True, it lets current go through the circuit, and the presence of current will indicate a True condition. If the switch's status is False, no current can go through it, and the absence of current will mean False.
If we put two switches one after the other, as in Panel (2) of the same figure, we see that the current can flow through only if both switches are True. So putting switches in series corresponds to creating an and circuit. The current will flow through the and circuit is Switch a is True, and if Switch b is True. If either one of them is False, no current flows through. You can verify with the truth table for the Boolean And function above that this is indeed the behavior of a boolean and operator. Verify for yourself that the third circuit in the figure implements a boolean or operator. The circuit lets current go through if Switch a is True or if Switch b is True.
In his thesis, Shannon presented the missing link, the bridge that would allow electrical/electronic computers to perform arithmetic computation. He demonstrated that if one were to map True and False values to 1 and 0 of the binary system, then the rules of arithmetic because logic rules. That mean adding two integers because a problem in logic, where assertions are either true or false.
Let's see how this actually works out. Remember the section above when we added two binary numbers together? Let's just concentrate on the bit that is the rightmost bit of both numbers (in computer science we refere to this bit as the least significant bit). If we are adding two bits together, and if both of them can be either 0 or 1, then we have 4 possible possibilities:
0 0 1 1 + 0 + 1 + 0 + 1 ---- ---- ---- ----
Using the rules we created above for adding two bits together, we get the following results:
0 0 1 1 + 0 + 1 + 0 + 1 ---- ---- ---- ---- 0 1 1 1 0
Let's take another step which, although it doesn't seem necessary, is absolutely essential. You notice that the last addition generates a carry, and the result is 10. We get two bits. Let's add a leading 0 to the other three resulting bits
0 0 1 1 <--- a + 0 + 1 + 0 + 1 <--- b ---- ---- ---- ---- 0 0 0 1 0 1 1 0 <--- S | +---- C
Let's call the first bit a, the second bit b, the sum bit S, and the extra bit that we just added C (for carry). Let's show the same information we have in the four above additions into a table, similar to the truth tables we used before where we were discussing boolean algebra.
| a | b | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Do you recognize anything? Anything looking familiar? If not, let's use a code, and change all the 1s for Ts and all the 0s for Fs, and split the table in two:
| a | b | C |
|---|---|---|
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
and
| a | b | S |
|---|---|---|
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | F |
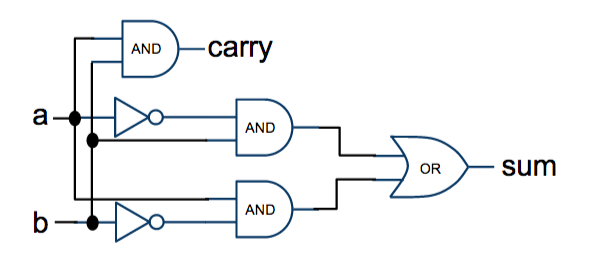
Now, if we observe the first table, we should recognize the table for the and operator! So it is true: arithmetic on bits can actually be done as a logic operation. But is it true of the S bit? We do not recognize the truth table of a known operator. But remember the ice cream example; we probably come up with a logic expression that matches this table. An easy way to come up with this expression is to express it in English first and then translate it into a logic expression:
- S is true in two cases: when a is true and b is false, or when a is false and b is true.
or
- S = ( a and not b ) or ( not a and b )
As an exercise you can generate the truth table for all the terms in this expression and see if their combinational expression here is the same as S.
So, here we are with our premises about our current computers and why they work. We have answered important questions and made significant discoveries, which we summarize below
Discoveries |
- Computers use electricity as a source of power, and use flows of electrons (electric currents) to convey information.
- Switches are used to control the flow of electrons, creating a system of two values based on whether the flow is ON or OFF.
- While the binary system uses only two digits it is just as powerful as the system of decimal numbers, allowing one to count, add, and do arithmetic operations with binary numbers.
- The boolean algebra is a system which also sports two values, true and false, and logical operators and well defined properties.
- Logic operator are easy to generate with electronic switches
- Arithmetic operations in binary can be expressed using the operators of the boolean algebra.
Logic Gates |
Now that Shannon had shown that computing operations (such as arithmetic) could be done with logic, engineers started creating special electronic circuits that implemented the basic logic operations: AND, OR, and NOT. Because the logical operators are universal, i.e. you can create any boolean function by combining the right logical operators with boolean variables, then these special circuits became universal circuits. We have a special name for them: gates.
A gate is simply an electronic circuit that uses electricity and implements a logic function. Instead of using True or False, though, we find it easier to replace True by 1 and False by 0.
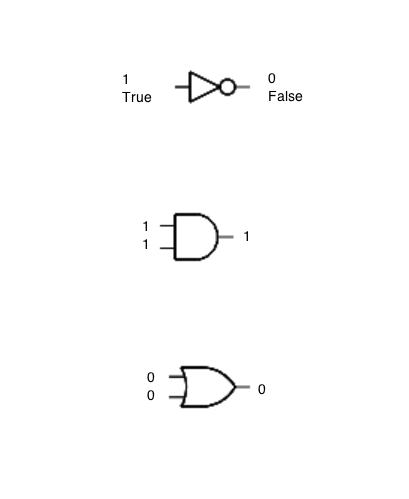
The gates have the same truth table as the logic operators they represent, except now we'll use 1s and 0s instead of T or F to represent them. For example, below is the truth table for the OR gate:
The truth table for the OR gate is the following:
| a | b | a or b |
|---|---|---|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
The truth table for the AND gate:
| a | b | a and b |
|---|---|---|
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
You should be able to figure out the table for the NOT gate, which we'll also refer to as an inverter gate, or simply inverter.
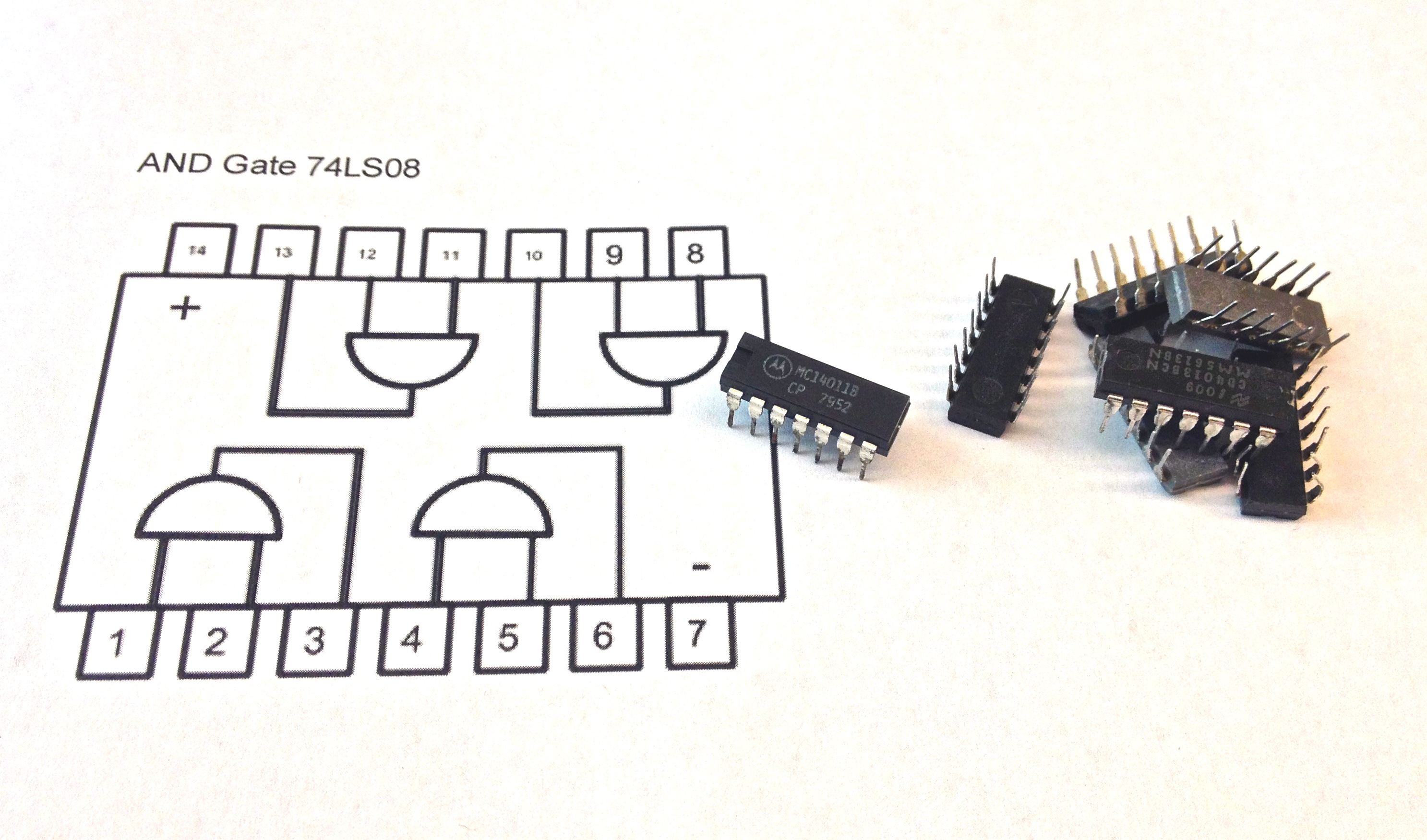
The image on the left, above, shows an integrated circuit (IC)close up. In reality the circuit is about as long as a quarter (and with newer technology even smaller). The image on the right shows what is inside the IC. Just 4 AND gates. There are other ICs that contain different types of gates, such as OR gates or Inverters.
Building a Two-Bit Adder with Logic Gates
Designing the schematics for an electronic circuit from boolean function is very easy once we do a few examples:
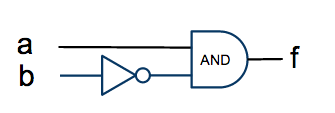
For example, imagine that we have a boolean function f of two variables a and b equal to:
- f = a AND ( NOT b )
To implement it with logic gates we make a and b inputs, and f the output of the circuit. Then b is fed into an inverter gate (NOT), and the output of the inverter into the input of an AND gate. The other input of the AND gate is connected to the a signal, and the output becomes f.
Given the equations for the sum and carry signals that we generated earlier, we can now compose them using logic gates as shown below:
Computer Simulator |
Time to Play A Game |
Let's assume that we want to play a very simple game based on coding. The game is quite easy to get: we want two people to have a conversation where each word or sentence that they can say is limited to a small set of preselected sentence, and each one is associated with a number. When the two people talk to each other, they must pick the number corresponding to the sentence, question, or answer they want to say.
Here's a list of numbers and their associated sentences:
00 Really? 01 Hello 00 No 02 How are you? 01 Yes 03 Did you enjoy... 02 Good 04 Was it good? 03 Bad 05 Have you finished... 04 A tiny bit 06 Do you like... 05 A lot 06 Homework 07 Wiki 08 Apples 09 Cereals 10 Bugs 11 Breakfast 12 PC Lab 13 Hello!
Now, you'll figure out quickly what the following two people are saying:
— 01 02
— 02
— 03 06
— 01 05
If you didn't figure it out, the first person was saying "Hello" and "How are you?" to which the second person responded "Good". The first person then continued with "Did you enjoy" and "homework", to with the second person responded "Yes" and "A lot"! (Definitely somebody overzealous with the class!)
What is important for us is to see that with this simple example we can create a code where we replace sentences or words by numbers. The same number can represent different sentences, but because of the context in which they are used, one can decode the dialog and figure out what was said.
Let's go one step further and add a counter next to each of the different sentences. Our dialog between our two interlocutors becomes
00: 01 02 01: 02 02: 03 06 03: 01 05
All we have done is simply put line numbers in front of each group of numbers said by the two people. It doesn't appear that it's helping us much, but it is actually a big steps, because now we can refer to each line by a number, and we get closer to creating an algorithm[6].
Let's add a new sentence and a number to our list:
20 Go back to...
Let's see if you can figure out where we are going with this. What does this new series of numbers mean?
00: 01 02 01: 02 02: 03 06 03: 01 05 04: 20 00
You probably guessed it: it's the same conversation as before, but at the end the 20 00 numbers instruct us to go back to Line 0 and we start the conversation again. Just like a movie playing in an endless loop. While this may not seem terribly interesting, it is actually quite powerful. Watch the exchange between the robot played by Robin Williams and his owner, played by Sam Neil in the 1999 movie Bicentenial Man". Here one of the two "people"
having a conversation is an ultra-logical being: a robot, who is not fully aware of the subtleties of the art of (human) conversation:
(advance the movie to 7 minutes and 10 seconds)
Let's go one step further and change the rules of our "game" slightly. Imagine that instead of two interlocutors, we have a prof and a whole class of students, and we'd like to describe only the prof's side of the conversation he or she is having with the whole class, and not the student's part. But remember, the rule is still to only use numbers. How can we indicate that the conversation should be with one person first, then with the next, then the next, and so on?
One way to make this happen is to introduce more coding in our game.
- we give a number to each student in the class, starting with 0 (in computer science we always like to start with 0 when we count) for the student who is closest to the left front corner of the room.
- we give the number 1 to the neighbor of Student 0, and keep giving numbers to everybody, in a logical way, until everybody in class has a number.
- we introduce new number and sentence combinations to our code:
30 Start with Person... 31 Move to next person
See where we're going? For this prof, the task of managing this conversation with the whole class (granted, it won't be a very original conversation) requires a few steps:
- pick the first person in the class (the one associated with Number 0).
- exchange a few sentences to this person ("hello")
- move on to the next person
- repeat the same conversation with this person.
Think a bit about this and see if you can come up with a algorithm or program that will allow for this conversation to take place.
Figured it out?
Ok, here's one possible answer.
00: 30 00 (Start with Person 0) 01: 01 02 (Hello, how are you) 02: 03 06 (Did you enjoy homework) 03: 31 (Move to next person) 04: 20 00 (Go back to Line 00)
So now, even though this simple game is far from sophisticated or even fully functional, it should illustrate the principles that are at play when a processor executes a program that resides in memory. We explore this in the next section. By the way, if while reading the last algorithm shown above you thought to yourself "Hmmm... something strange is going to happen when we reach the last student in the class...", then you have a very logical mind, and Yes, indeed, you are right, our algorithm is not quite correct. But it has allowed us to get the idea of what's ahead of us.
Computer Memory |
We are very close to looking into how the processor runs programs. We have seen that computers work with electricity, and that information is coded as 0s and 1s. We refer to an information cell that contains a 0 or a 1 as a bit. The memory is a collection of boxes that contain bits. We refer to these boxes as words, or Memory words.
Now is a good time for a bit of magic! The magic requires building a simple circuit with AND and NOT gates, as shown below:

You may want to spend the time building it up with our circuit simulator.
When you have your circuit built, why don't you turn the power on and activate the two inputs (on the left) randomly, and when you are done, bring the two inputs back to 1 1, i.e. both red. Observe the output. Is it red? black? Make a note of it. Now activate the inputs again, randomly, bringing them back to 1 1 (red red) at the end of your experiment. Chances are the output will be different from the last time you stopped. This is pretty amazing if you think about it. We are using logic circuit, gates that implement the truth table of mathematically immutable laws, the laws of logic, but this circuit that we have built does not always output the same result, even when the two inputs are identical.
Below is an image of the same circuit with a different output:
When you play some more with this circuit you will discover that what it does is remember which input is the last one you set to 0. If the last input that was 0 before you brought both of them back to 1 1 is the top input, then the output will be 1 (red). If the last input that was 0 is the bottom one, then the output will be 0 (black).
This circuit has memory! That's magic. We are using purely combinational gates, gates that have no memory whatsoever in them, but by creating a cycle (look for the figure 8 in the logic diagram above) with the wiring, we create a feedback loop that helps information cycle around the loop. We won't study this more, as it is beyond the scope of our study, but if you are interested in this circuit, it is referred to in digital design as a flipflop. The idea is that it behaves like a scale with two platters to weigh produce. The scale can be tilting left, or tilting right, and remains stable in that state until one of the inputs is activated. That's the idea of a digital flipflop. We are in the presence of a memory bit! Bits in computers are implemented with similar circuits.

A bit of trivia: when you have 4 bits together, for example 1011, this group of four bits is called a nybble (note the y instead of the i). When we have a grouping of 8 bits, this is called a byte (again, note the y instead of the i). When we have more, the definitions get a bit loose, and we usually refer them as words, specifying how many bits they contain. For example: 16-bit words, or 32-bit words, or 64-bit words. The Intel or AMD processor inside your laptop or desktop computer operates with 32- and 64-bit words.
The memory is a collection of billions of memory words, each one storing a collection of bits. We saw earlier that a collection of bits can actually represents a binary number, and each binary number has an equivalent decimal number. So we can actually say that the memory is a collection of cells that contain numbers. It's easier for us human beings to deal with decimal numbers, so that's what we are going to do in the remainder of this section, but actually all the numbers in questions are binary. Does it make sense?
So, here's how we can view the memory:
+-------------+ 1000000000 | 45 | +-------------+ . . . . . . +-------------+ 10 | 1103 | +-------------+ 9 | 0 | +-------------+ 8 | 7 | +-------------+ 7 | 1 | +-------------+ 6 | 13 | +-------------+ 5 | 7 | +-------------+ 4 | 0 | +-------------+ 3 | 10 | +-------------+ 2 | 5 | +-------------+ 1 | 103 | +-------------+ 0 | 3 | +-------------+
It's a long structure made up of binary words. Words are numbered, from 0, to a large number, which is actually equal to the size of the memory, in increments of 1. When you read the sticker for a computer on sale at the local store, it may say that the computer contains 4 Gigabytes of RAM. What this means is that the memory, the Random Access Memory (RAM), is comprised of words containing numbers, the first one associated with a label of 0, the last one with a label (almost) equal to 4,000,000,000. By the way, Giga means billion, Mega, million, and Kilo, a thousand.
Now that we are more familiar with the memory and how it is organized, we switch to the processor.
The Processor |
Before we figure out what kind of number code the processor can understand, let's talk for an instant about the role of the processor relative to the memory. The processor is a machine that constantly reads numbers from memory. It normally starts with the word stored in the cell with label 0 (we'll say the memory cell at Address 0), reads its contents, then moves on to the next word at Address 1, then the next one at Address 2, and so on. In order to keep track of where to go next, it keeps the address of the cell it is going to access in a special word it keeps internally called Program Counter, or PC for short. PC is a special memory word that is inside the processor. It doesn't have an address. We call such memory words when they are inside the processor registers.
- Definition
- A register is a memory word inside the processor. A processor contains only a handful of registers.
The processor has three important registers that allow it to work in this machine-like fashion: the PC, the Accumulator (shortened to AC), and the Instruction Register (IR for short). The PC is used to "point" to the address in memory of the next word to bring in. When this number enters the processor, it must be stored somewhere so that the processor can figure out what kind of action to take. This holding place is the IR register. The way the AC register works is best illustrated by the way we use a regular hand calculator. Whenever you enter a number into a calculator, it appears in the display of the calculator, indicating that the calculator actually holds this value somewhere internally. When you type a new number that you want to add to the first one, the first number disappears from the display, but you know it is kept inside because as soon as you press the = key the sum of the first and of the second number appears in the display. It means that while the calculator was displaying the second number you had typed, it still had the first number stored somewhere internally. For the processor there is a similar register used to keep intermediate results. That's the AC register.
All the processor gets from these memory cells it reads are numbers. Remember, that's the only thing we can actually create in a computer: groups of bits. So each memory cell's number is read by the processor. How does the number move from memory to the processor? The answer: on metal wires, each wire transferring one bit of the number. If you have ever taken a computer apart and taken a look at its motherboard, you will have seen such wires. They are there for bits to travel back and forth between the different parts of the computer, and in particular between the processor and the memory. The image to the right shows the wires carrying the bits (photo courtesy of www.inkity.com). Even though it seems that some wires do not go anywhere, they actually connect to tiny holes that go through the motherboard and allow them to continue on the other side, allowing wires to cross each other without touching.).
In summary, the processor is designed to quickly access all the memory words in series, and absorbs the numbers that they contain. And it does this very fast and automatically. But what does it do with the numbers, and what do the numbers mean to the processor?
These numbers form a code. The same type of code we used in the silly game we introduced earlier. Just as we could have numbers coding sentences of a conversation, different numbers will mean different actions for the processor to take . We are going to refer to these actions as instructions.
- Definitions
- The collection of instructions as a program. A program implements an algorithm, which is a description of how a result should be computed without specifying the actual nitty gritty details.
- The set of all the instructions and the rules for how to use them is a called assembly language.
But there is another subtlety here. Not all numbers are instructions. Just as in our games some numbers corresponded to sentences and others words that needed to be added at end of sentences ("did you like", "homework" for example), some numbers represent actions, while others are just regular numbers. When the processor starts absorbing the contents of memory cells, it assumes that the first number it's going to get is an instruction. An instruction is usually followed by a datum. A program is thus a collection of instructions and data.
Thinking of the memory as holding binary numbers that can be instructions or data, and that are organized in a logical way so that the processor always knows which is which was first conceived by John von Neumann in a famous report he wrote in 1945 titled "First Draft of a Report on the EDVAC" [1]. This report was not officially published until 1993, but circulated among the engineers of the time and his recommendations for how to design a computing machines are still the base of today's computer design. In his report he suggested that computers should store the code and the data in the same medium, which he called store at the time, but which we refer to as memory now. He suggested that the computer should have a unit dealing with understanding the instructions and executing them (the control unit) and a unit dedicated to perform operations (today's arithmetic and logic unit). He also suggested the idea that such a machine needed to be connected to peripherals for inputting programs and outputting results. This is the way modern computers are designed.
The Cookie Monster Analogy |
The processor is just like the cookie monster. But a cookie monster acting like Pac-Man, a Pac-Man that follows a straight path made of big slabs of cement, where there's a cookie on each slab. Our Cookie-Monster-Pac-Man always starts on the first slab, which is labeled 0, grabs the cookie, eats it, then moves on to Slab 1, grabs the cookie there, eats it, and keeps on going!
The processor, you will have guessed, uses the memory words as the slabs. It always starts by going to the memory word at Address 0. It does this because the Program Counter register (PC) is always going to be reset to 0 before the processor starts executing a program. The processor sends the address 0 to memory, grabs the number that it finds at that location, puts it in the IR register for safe keeping, eats it to figure out what that number means, what action needs to be performed, and then performs that action.
That's it! That's the only thing a processor ever does!
Well, almost the only thing. While it is performing the action, it also increments the PC register by 1, so that now the PC register contains 1, and the processor will repeat the same series of steps, but this time will go fetch the contents of Memory Location 1.
This means that the numbers that are stored in memory represent some action to be performed by the
processor. They implement a code. That code defines a language. We call it Assembly Language.
Instead of trying to remember the number associated with an action, we use a short word, a mnemonic
that is much easier to remember than the number. Writing a series of mnemonics to instruct the processor
to execute a series of action is the process of writing an assembly-language program.
Instructions and Assembly Language |
The first mnemonic we will look at is LOD-C n. It means LOAD a Constant into the AC register. LOD-C
is always followed by a number.
LOD-C 3
The instruction above, for example, means load the number 3 into the AC register.
LOD-C 11
The instruction above means load the number 11 into AC.
Before we write a small program we need to learn a couple more instructions.
STO 10
The STO n mnemonic, or instruction, is always followed by a number representing an address in memory. It means STOre the contents of the AC register in memory at the location specified by the number. So STO 10 tells the processor "Store AC in memory at Address 10", or, "Store AC at Address 10" for short.
ADD 11
The ADD n mnemonic is also always followed by a number representing an address. I means "ADD the contents of Memory Location n to the AC register", or "ADD contents of Address n to AC".
It is now time to write our first program. We will use the simulator from
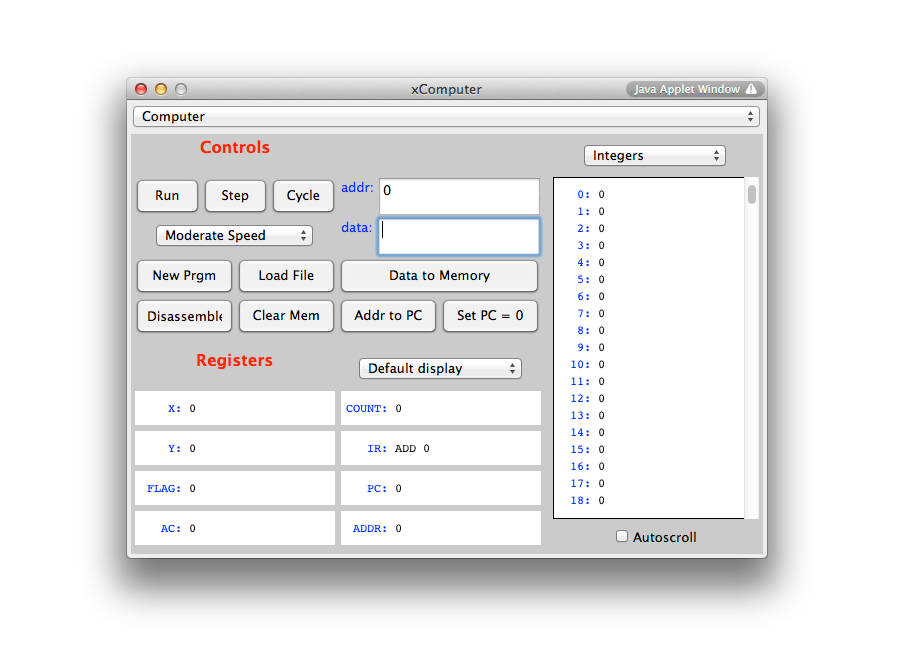
our applet page. When you start it you the window shown below.
An illustrated view of the simulator applet is given below:
A First Program |
Let's write a program that takes two numbers stored in memory, adds them up together, and stores their sum in a third number. When we deal with memory locations that contain numbers (our data), we refer to them as variables. So another way of phrasing our problem is this:
- Let's write a program that adds two variables together and stores their sum in a third variable.
Our program is below:
@0
LOD 10
ADD 11
STO 12
HLT
@10
3
5
0
That's it. That's our first program. If we enter it in the program window of the simulator, and then translate the program into instructions stored in memory, and then run the program, we should end up with the number 8 appearing in memory at Address 12.
Let's decipher the program first:
| Instructions | Explanations |
|---|---|
@0 |
This line instructs the translator or compiler that will take this program and generate a list of instructions in memory that it should store the next instructions at Address 0. Programs always start at 0. |
LOD 10 |
Load the variable at Address 10 into the AC register. Whatever AC's original value, after this instruction it will contain whatever is stored at Address 10. We'll see in a few moments that the number is 2. So AC will contain 2. |
ADD 11 |
Get the variable at Address 11 and add the number found to the number in the AC register. The AC register's value becomes 2 + 3 or 5. |
STO 12 |
Store the contents of the AC at Address 12. Since AC contains 5, the number is copied in the variable at Address 12. |
HLT |
|
|
|
|
@10 |
We now indicate to the translator that the next information should be stored starting at a new address, in this case Address 10. |
3 |
|
5 |
The number 5 should be stored at memory Address 11. Why 11? Because the previous variable was at Address 10. |
0 |
This 0 represents the third variable that will hold the sum of the first two variables. We store 0 because we want to have some value there when the program starts. And because we know the program is supposed to store 8 in this variable, we pick a number different from 8. 0 is often a good value to initialize variables with. |
We now use the simulator to write the program, translate it, and to execute it.
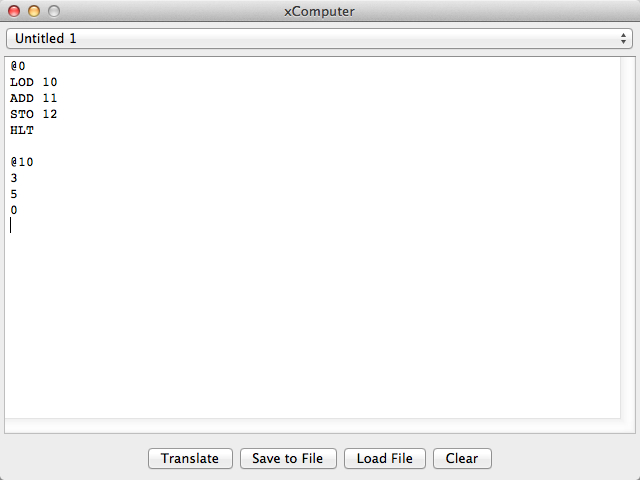
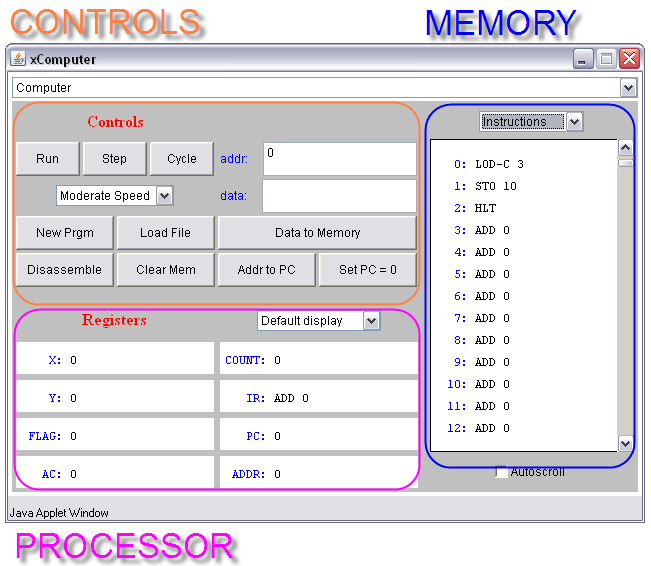
The figure above shows the program entered in the Program Window of the simulator. It is entered simply by typing the information in the window as one would write a paper, or letter. Programs are texts. They are written using a particular coding system (in our case assembly language), and a translator must be invoked to transform the text into numbers.
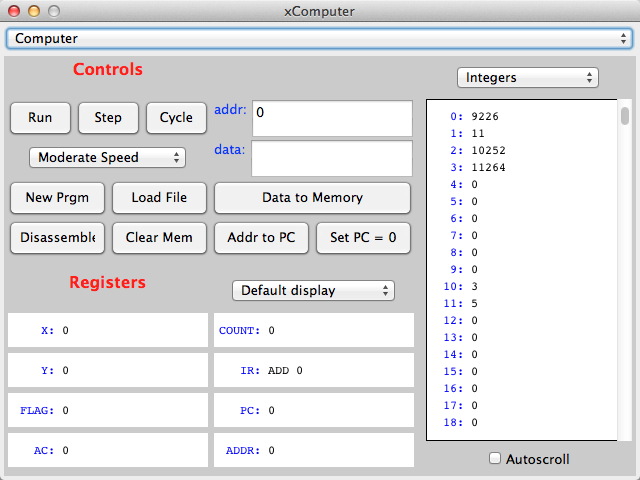
The figure above shows the result of pressing the Translate button. The translator takes the program, transforms each line into a number, and stores the numbers at different addresses in memory. You should recognize 3 numbers at Addresses 10, 11, and 12. Yes?
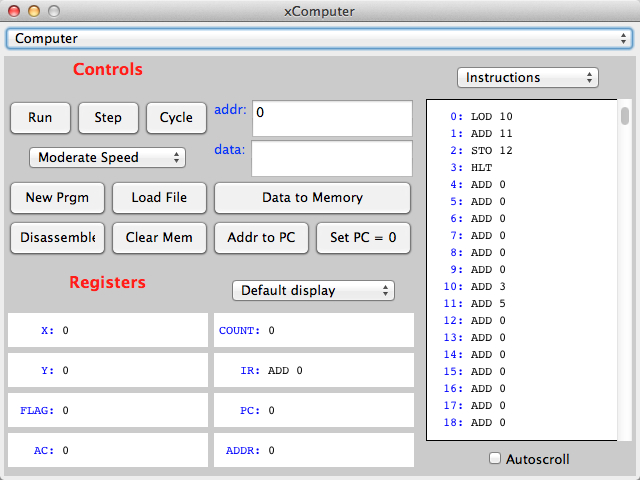
The figure above shows the same information as displayed in the previous image, but this time we have asked the simulator
to show the contents of memory as instructions. The simulator looks at each number in the memory and simply does a reverse translation. The problem for us is that the simulator does not understand our logic. It doesn't know that we divided our program into two separate parts: the instructions and the data, and that they are at different memory location. If we ask
the simulator to display the contents of memory as instructions, it does so, and not only reverse-decodes the instructions correctly into LOD, ADD, STO, and HLT, but it takes all the other numbers and figures out what instructions would
correspond to these numbers, even though our program doesn't have more instructions. So 3 becomes ADD 3,
5 becomes Add 5 and 0 becomes Add 0.

If we press on the Run button, the simulator starts going and executes the program, step-by-step, very fast. The figure
above shows the simulator when it has finished running the program. We know that the program has finished running because
the legend Clock Stopped appears in the top of the simulator window. The simulator always does this when it executes
a HLT instruction. Note that ADD 8 now appears in Memory Location 12. It should really be 8, but we see ADD 8. That is simply because the simulator is in this mode where it shows every number as an instruction. If we want to see the numbers, then we switch the simulator to make it display numbers, and that's the figure below.
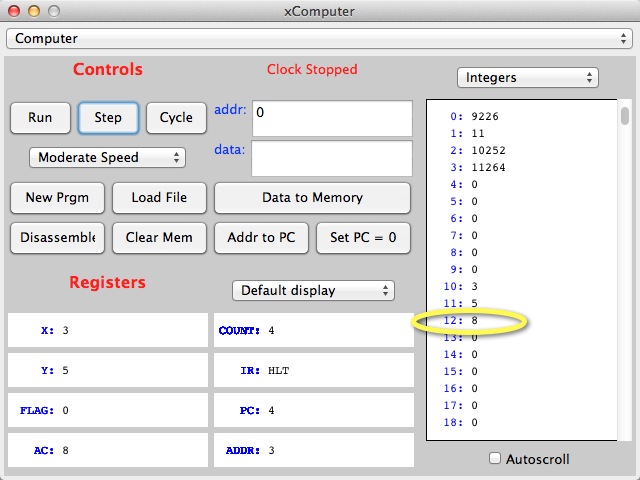
At this point you should continue with the laboratory
prepared for this topic. It will take you step by step through the process of creating programs
in assembly language for this simulated processor.
The list of all the instructions available for this processor is given below:
Note "-C" means Constant
ADD Add to Acc ADD-C Add C to Acc SUB Sub from Acc SUB-C Sub C from Acc AND And with Acc AND-C And C with Acc OR Or with Acc OR-C Or C with Acc NOT invert Acc LOD-C Load C in Acc SHL Shift left Acc ADD-I Add-indirect SHR Shift right Acc SUB-I Sub-indirect INC Increment Acc AND-I And-indirect DEC Decrement Acc OR-I Or-indirect LOD Load Acc from mem LOD-I Load indirect HLT Stop! STO-I Store indirect JMP Jmp to address JMP-I Jmp indirect JMZ Jmp if Acc=0 JMZ-I Jmp zero indirect JMN Jmp if negative JMN-I Jmp negative indirect JMF Jmp on flag JMF-I Jmp flag indirect STO Store Acc in mem
We won't learn all of the them. The ones we touched on in the lab is sufficient to understand how a processor works.
Studying an Assembly Language Program
Let's take the solution program for the last problem of the laboratory you just did and go through it, one instruction at a time.
This program The program is the following:
; Solution for Problem 5 ; D. Thiebaut ; First initialize both variables with 55 start: lod-c 55 sto 15 sto 16 ; now loop and increment Location 15 and decrement Location 16 ; the loop is endless. loop: lod 15 add-c 1 sto 15 lod 16 dec sto 16 jmp loop hlt @15 0 0
First, the lines starting with semi colons are comments, and not part of the actual program. They allow the programmers
to add extra information for other programmers who may read the code.
| instructions | Comments |
|---|---|
start: lod-c 55 |
Start: is a label. It is a word we choose that cannot be confused with an instruction. It is a way of documenting the program. The instruction loads the constant 55 into the AC register. |
sto 15
sto 16
|
store the contents of the AC register (which now contains 55) at Memory Locations 15 and 16. |
; now loop... ; the loop is ... |
Two comments to indicate what is going on next. |
loop: lod 15 |
We give a name to the current memory location and call it "loop". The instruction tells the processor to go to Address 15 and load the number there into AC. |
add-c 1 |
Add the constant 1 to AC. |
sto 15 |
Store AC back at memory location 15 |
lod 16 |
Now load the contents of Memory Location 16 into AC. |
dec |
Decrement AC by 1 (always by 1 for INC and DEC) |
sto 16 |
Store AC back at Memory Location 16. |
jmp loop |
Force the processor to set its PC register to the address corresponding to the loop label. The processor will go back to this address and execute the lod 15 instruction. |
hlt |
Halt. The processor will stop when it reaches this instruction. But... because we have a program with an endless or infinite loop, the processor will never reach this instruction. Nonetheless, it is good practice to always have a HLT instruction to mark the end of a program. |
@15 |
We now indicate that we are going to store some variables starting at Address 15. |
0 |
The word at Memory Location 15 is initialized with 0. |
0 |
The word at Memory Location 16 (next logical address after 15) is initialized with 0 as well. |
Summary/Points to Remember |
Here we summarize the important points you should remember from this section.
- All we are going to find inside a computer are numbers. Binary numbers. The reason is that computers work with electricity, and the only way we have to store information will be using gates wired as flipflops, which allow us to store individual bits, and we can modify binary information using circuits similar to adders, and we saw that they can easily been built using logic gates.
- It is tempting to think that characters such as 'A', 'B', etc are stored in memory at some point. But actually they are not. There is a special code that assigns numbers to letters, and these are the numbers we find in memory. Again, these are binary numbers. You may have heard of the code used to assign numbers to characters. It is called ASCII, or American Standard Code for Information Interchange. It is an old code that was created for English-based languages. The Unicode is now replacing ASCII in many applications, as it allows one to represent many more languages that have different character sets (such as Japanese, Chinese, etc.)
- The processor can execute three basic types of instructions.
- data move instructions that moves information from one place in the computer to another place. The LOD and STO instructions are good examples of this group.
- arithmetic instructions, such as the ADD-C or ADD, which performs the addition of some quantity to the contents of the AC register.
- control instructions, such as JMP, that instructs the processor not to continue at the next memory location when it comes time to fetch a new instruction, but to go to a different address.
- Instructions are very unsophisticated. They are very basic and operates on 1 number at a time, and modify this number using very basic operations: an addition, a subtraction, changing the value.
- However, the processor is very fast at executing these instructions. a 1 GHz (gigahertz) processor can execute 1 billion such instruction per second. If a human being capable of executing 1 action every second was asked to execute 1 billion such actions, without ever stopping for sleep, this would take that person... (let's ask Wolfram Alpha)
- 31 years! Imagine what a person could do in 31 years, without ever stopping or sleeping! Even if the actions are very simple, such as laying bricks or stones one on top of the other: 31 years of masonry would create quite a castle! Processors build the equivalent of castles for us every second! And they are predictable in their outcome.
The Von Neumann Bottleneck |
We are now coming back to John Von Neumann in an effort to understand the concept of the Von Neumann Bottleneck, a term that appears from time to time in newspaper articles for the general public, such as this article from Steve Lohr in the New York Times Bits section, titled "Big Data, Speed, and the Future of Computing", published Oct 31 2011[7].
John Von Neumann, if you remember, is this brilliant mathematician and renaissance man who in 1945, after having studied the design of the EDVAC computing machine at the Moore School of Electrical Engineering at the University of Pennsylvania wrote a report with his recommendations for how a computing machine should be organized and built. There are many remarkable things about this report:
- The first is that it was the synthesis of many different good ideas of the time from the few people who were involved in building such machines, and as such it presented some form of blueprint for machines to come.
- Even more remarkable is that the draft was never officially published but circulated well within the small group of experts interested in the subject, and when new research group started getting interested in building calculating machines, they would use the report as a guide.
- Possibly the most remarkable about Von Neumann's design is that chances are very high that the computer you are currently using to read this document (laptop, desktop, tablet, phone) contains a processor built on these original principles!
These principles were that good! And they offered such an attractive design that for the past 70 years or so, engineers have kept building computers this way.
So what is this bottleneck and why is it bad?
Before we answer this question, we have to understand that we human beings have had an ever increasing thirst for more and more complex programs that would solve more and more complex problems. And this appetite for solving larger and more complex problems has basically forced the computers to evolve in two simple complementary ways. The first is that computers have had to be faster with each new generation, and the second is that the size of the memory has had to increase with every new generation as well.
Nate Silver provides a very good example illustrating these complementary pressures on computer hardware in his book The Signal and the Noise[8]. The recent hurricanes have shown an interesting competition between different models of weather prediction, and in particular the path of hurricanes over populated areas. Some models are European, others American, and super storm Sandy in October 2012 illustrated that some models were better predictors than others. In this particular case, the European models predicted the path of Sandy more accurately than their counterparts. Since then, there has been a push on the National Center for Atmospheric Research (NCAR) to update its computing power in order to increase the accuracy of its model. How are the two related?
The reason is that to predict the weather one has to divide the earth into quadrants forming large squares in a grid covering the earth. Each square delimits an area of the earth for which many parameters are recorded using various sensors and technologies (temperature, humidity, daylight, cloud coverage, wind speed, etc). A series of equations links the influence that each parameter in a cell of the grid exerts on the parameters of neighboring cells, and a computer model simply looks at how different parameters have evolved in a give cell of the grid over a period of time, and how they are likely to continue evolving in the future. The larger the grid size, though, the more approximate the prediction. A better way to enhance the prediction is to make the size of the grid smaller. For example, one could divide the side of each square in the grid by half. If we do that, though, this makes the number of cells in the grid increase by a factor of four. If you are not sure why, draw a square on a piece of paper and then divide the square in half vertically and in half horizontally: you will get 4 smaller squares inside the original one. What does that mean for the computation of the weather prediction, tough? Well, if we have 4 times more squares, then we need four times more data for each cell of the new grid, and there will be 4 times more computation to be performed. But wait! The weather does not happen only at ground level; it also takes place in the atmosphere. So our grid is not a grid of squares, but a three-dimensional grid of cubes. And if we divide the side of each cube in half, we get eight new sub-cubes. So we need actually eight times more data, and we will have eight times more computation to perform. But wait! There is also another element that comes into play: time! Winds travel at a given speed. So the computation that expects wind to enter the side of our original cube at some period of time and exit the opposite side of a cube some interval of time later needs to be performed more often, since that same wind will now cross a sub-cube of the grid twice as fast as before. So in short, if the NCAR decides to refine the size of the grid it uses to compute its weather prediction, and divides it by two, it will have 8 x 2 = 16 times more computation to performed. And since weather prediction takes a lot of time and should be done in no more than 24 hours to actually have a good chance to predict the weather tomorrow, that means that performing 16 times more computation in the same 24 hours will require a new computer with:
- a processor 16 times faster than the last computer used,
- a memory that can hold 8 times more data than previously.
Nate Silver makes the clever observation that since computer performance has been doubling roughly every two years[9], getting an increase of 16 in performance requires buying a new computer after 8 years, which is roughly the frequency with which NCAR upgrades its main computers!
So computers have had to evolve fast to keep up with our increasing sophistication in what we get and what we expect from them.
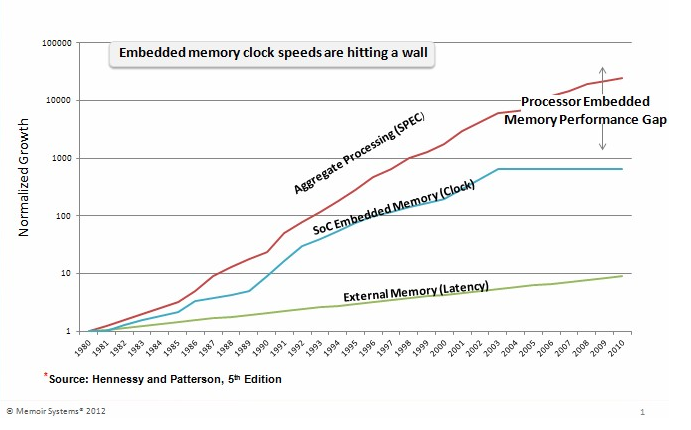
But there's a problem with the speed at which processors and memory have improved. While processors have doubled performance every two years for almost four decades now, memory has not. At least not as fast, and it appears that it is now not improving at all. The figure below taken from an article by Sundar Iyer for EETimes[10] shows the gap existing between the performance of processors compared to that of memory. The bad news is that the processor has been getting faster at doing computation, but memory has not been able to keep up the pace, so processors are in effect limited and it doesn't seem that there is a solution in sight. At least not one that uses the currently semiconductor technology.
That's one of the limiting aspects of the Von Neumann bottleneck. Using our previous metaphor of the cookie monster, it is akin to having our cookie monster walking on a treadmill where cookies are dropped in front of him at regular intervals, and the cookie monster is becoming faster and faster at walking the treadmill and eating cookies, but the treadmill, while increasing in speed as well, is not able to keep up with the cookie monster.
The second limiting problem of the Von Neumann bottleneck is in the way the processor in a computer is the center of activities for everything. Everything has to go through it. Instructions, data, everything that is in memory is for the processor. The processor is going to have to access it, read it, modify it at least once during their time in memory. And sometimes multiple times. So this is a huge demand on the processor. Remember the Accumulator register (AC) in our processor simulator? Any data whatsoever that is in memory at some point will have to go into AC to be either moved somewhere else or modified. To get an idea of what this represent, imagine that the size of the AC register is the size of a dime. Since a register is a memory word, then the size of a memory word would be the same. In today's computers, the Random Access Memory (RAM) contains from 4 billion to 8 billion memory words. 4 billion dimes would cover the size of a football field. Von Neumann gave us a design where the computation is done in a tiny area while the data spans a huge area, and there is not other way to process the data than to bring them into the processor. That's the second aspect of the Von Neumann bottleneck.
There has been attempts at breaking this design flaw, and some have helped performance to some extent, but we are still facing a major challenge with the bottleneck. Possibly the most successful design change has been the replication of processors on the chip. Intel and other manufacturers have created duo-core, quad-core, octa-core, and other design where 2, 4, 8 or more processors, or cores, are grouped together on the same piece of silicon, inside the same integrated circuit. Such designs are complex because these cores may have to share access to the memory, and have to be careful when operating on the same data (sharing data). While improvements in performance have been encouraging, some research has hinted that the performance would decrease as the number of cores increases, as illustrated in the graph below taken from an article by Samuel K. Moore[11], where we see that in a simulation of the performance of systems with 2, 4, 8, 16 and 32 cores, the conflict of accessing the memory at the same time by the different core would dramatically reduce their performance. None-the-less, Intel and other manufacturers are not deterred and feel better software tools will be created to better harness to potential of multi-core processors.
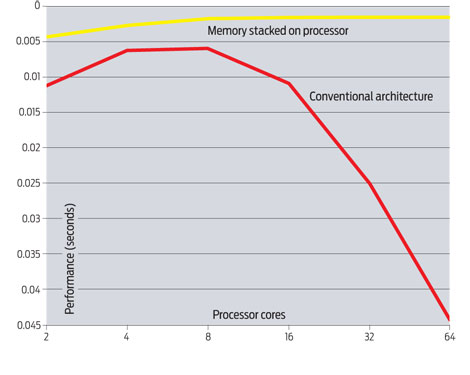
Moore's Law |
To understand Moore's Law we need to understand exponential growth first. In our context, it makes sense to consider quantities that grow over time, but exponential growth applies to a broader spectrum of things. However, if you understand exponential growth in our context, its application to other areas will make sense.
Exponential Growth
Something has an exponential growth if its size is doubling every fixed interval of time. A cute puzzle for which people often get the wrong answer will get us started.
- Suppose a lily is in the middle of a pond, and every day it doubles in size. In 30 days the lily has covered half of the pond. How long will it take it to cover the whole pond?
If you answered 31 days, then congratulations! Indeed, if it doubles in size every day, then after Day 30 it will be twice half the size of the pond, so it will have covered the whole pond! This simple example shows the powerful nature of exponential growth. It took the lily 30 days to cover 50% of the lake, but it takes in only 1 day to cover the other 50%.
There are many such puzzles in our cultures that attempt to demonstrate the extraordinary power of exponential growth through seemingly impossible feats. Another one is the story of grains of rice on a chessboard as told by David R. Henderson and Charles L. Hooper[12]:
- In a time of hunger, the Emperor of China wanted to repay a peasant who had saved the life of his child. The peasant could have any reward he chose, but the Emperor laughed when he heard the silly payment the foolish peasant selected: rice on a chessboard. The peasant wanted one grain of rice on the first square, doubling to two on the second, doubling to four on the third, and so on. After the Emperor agreed, his servants brought one bag of rice into his court and began tediously counting rice. Soon, he called for more and more bags of rice...
It turns out that it is impossible to grant such as wish, as the number of grains that would have to be put on the 64th square of the 8-by-8 chessboard is 2 times 2 times 2 times 2... 63 times. That is a series of 63 numbers 2 multiplying each other. That is 263, or 9,223,372,036,854,775,808, or 9 quintillion! Much more than the quantity of rice produced on earth in a single year.
Let's stay with this second example and write down the number of the square followed by the quantity of grains of rice:
| square | grains |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 16 |
| 6 | 32 |
| ... | ... |
The left column represents the number of the square being covered, and this number increases by 1 every time. The second column represents the quantity of interest, the number of grains, and doubles every time. So that is the setup for studying our exponential growth: something that doubles in size every fixed interval, in our case every new square.
Let's plot these numbers to observe their growth (plots generated with R).
Note the quick growth of the points in the graph. To get the full impact of the exponential growth we need to plot a few more points, first from Square 1 to 13, then from Square 1 to 25, and finally from Square 1 all the way to 64, as illustrated in the plots below:
What is important to see here is that as we show more and more squares, the actual growth that takes place for squares of low order, say, less than 40, is completely obfuscated by the large size of the quantities associated with the squares of higher order,
even though the number of grains on the 40th square is an impressive 549,755,813,888!
The last plot in the series, where all the squares from 1 to 64 are shown actually flattens everything except for Squares 55 and up. It also shows why people have referred to exponential-growth curves as "hockey-stick" curves, for the long flat growth and sudden turn upward, as this picture of a hockey stick below perfectly illustrates.

So, is there a better way to display the growth of the number of grains of rice over the complete range of squares of the chessboard, one that would show that there was growth at all levels? The answer is yes. We can use a logarithmic scale to display the quantities of grains. In a logarithmic scale, numbers are arranged in such a way that any pair of numbers that are related to each other in such a way that one is half the size of the other will always be the same distance from each other on the scale. The figure below shows a horizontal logarithmic scale.

This scale "squishes" very large numbers and emphasizes smaller ones. The next figure illustrates the property that the distance between any number and the one that is its double is constant. For example the distance between 4 and 8, 20 and 40, or 100 and 200 is the same in all three cases.

What happens when we apply this way of scaling the y-axis of the plot of the number of grains for all 64 squares of the chessboard is pretty remarkable.
With a logarithmic scale for the y-axis, an exponential growth appears as a straight line. And now the relationship that exists between the amounts of grains on the squares of low order is plainly visible. The logarithmic scale is the key to fully expose the property of exponential growths, and exposes them as straight line in a plot where the x-axis is linear (what we normally use for simple graphs), and the y-axis logarithmic.
Moore's Law
Gordon E. Moore, the co-founder of Intel, is credited with the observation that the number of transistors in integrated circuits had doubled every 18 months since 1958 to 1965[13]. At the time Moore predicted that the trend would continue for "at least 10 more years."
Almost 50 years later the trend has held remarkably well, as illustrated by the diagram below taken from NJTechReviews.com.
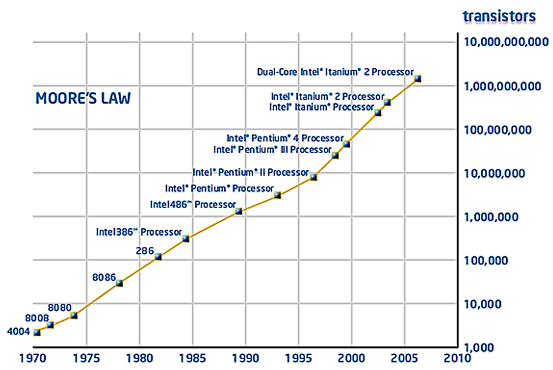
Notice that the growth of the number of transistors is quite straight in this logarithmic plot. It doesn't really matter that it is not absolutely straight. It is straight enough to se that the number of transistors has double, indeed, every 18 months or so over many decades. This is a very remarkable trend that has been observed in different areas associated with computer technology.
We saw very similar straight lines when we were discussing the Von Neumann bottleneck. The curves didn't show the growth of the number of transistors but the performance of the CPU and of the RAM. The performance is usually measured by the amount of instructions processed per second, or the amount of data accessed per second, and it is interesting to see that these quantities have grown exponentially as well.
The End of Moore's Law
The article "The End of Moore's Law"[14] that appeared in August 2013 in Forbes is typical of many articles that have been published for many years, and will continue being published for years to come.
The main point that these authors are making is that when you have an exponential law, the quantity measured at some point becomes such that it becomes physically impossible to exist. For example, if you look at transistors, the number of transistors being packed in a surface that is roughly 1 square inch is now surpassing the billion mark. That means that the size of the individual transistors is becoming smaller, and smaller, and smaller, and at some point they will reach the size of a few atoms. And because we can't build anything (yet) smaller than atoms, we will be stuck, and the law will abruptly stop its trend.
There is a very nice video from Intel showing the fabrication process of integrated circuits. You will notice at some point that the process of making an integrated circuit relies on depositing layers of material, sometimes metal, sometimes semiconductor, radiating it with some form of electromagnetic wave, and then removing different patterns of layers with acid. By repeating the process a very intricate network is created, linking different transistors to each other into blocks, and linking blocks with other blocks. The movie gives a good sense of the overwhelming complexity of the structure that results. When you have more than a billion transistors in a square inch connected together by a giant network of wires, some limits are becoming real.
So the point made by articles predicting the end of Moore's law simply state that we are designing ever smaller transistors and that the size of an atom is on the horizon. The Forbes article puts the end of Moore's law at around 2020.
Introduction to the Language Processing |
Fry and Reas present a nice and concise introduction to Processing in [15]. Quoting from their paper:
Processing is a programming language and environment built for the media arts communities. It is created to teach fundamentals of computer programming within the media arts context and to serve as a software sketchbook. It is used by students, artists, designers, architects, and researchers for learning, prototyping, and production. This essay discusses the ideas underlying the software and presents its relationship to open source software and the idea of software literacy. Additionally, Processing is discussed in relation to education and online communities.
How does Processing work? |
General Block Diagram
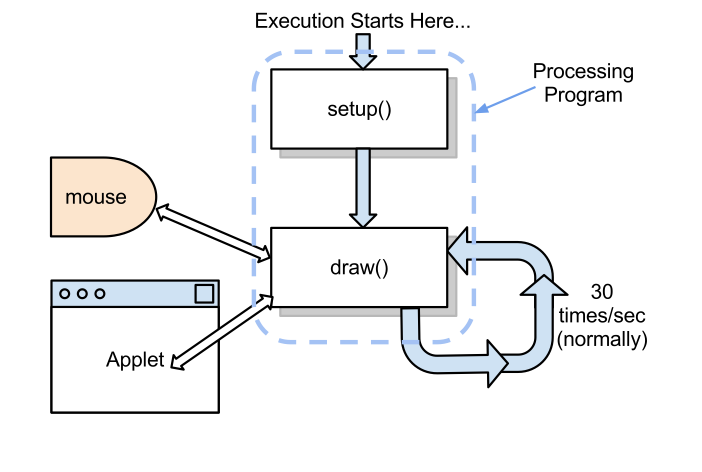
When a Processing program is started, two actions take place:
- the setup() function is executed by the processor. This happens only once. This is always the first action taken, and for this reason this function is a good place to put code that will define the shape of the applet, and anything settings that will remain constant throughout the execution of the program
- the draw() function is executed. And as soon as it is finished, it is restarted again. In general the repeat rate is 30 times per second, corresponding to a frame rate fast enough for our human eyes not to see the flickering.
Processing is a language that is built on top of another language: Java. Java is compatible with all three major operating systems (Windows, OS X, or Linux), and is free. Java is also superior for its graphing abilities. All these properties made it a good support language for Fry and Reas to pick when they wanted to create Processing.
Where does a Processing Program actually run?
The short answer: on your computer! If you are looking at a Processing applet that is running on a Web site, then the applet is downloaded first by the browser, and run inside the browser. If you are running a Processing program that you just created with the Processing editor, then it's also running on your computer. Because it is running on your computer, it can easily perform many useful tasks for programmers:
- Get characters typed at the keyboard
- Listen to what the mouse is doing, including changing its position, or whether buttons are pushed, clicked, or released.
- Display graphic shapes on the display window
- Play sound files (e.g. MP3 files)
- Play video files
- etc... (see the exhibition page on Processing for additional examples of interactions).
Writing a Processing Sketch
In Processing, programs are called sketches.
First we need to download and install Processing on our computer. See the Processing Download page for more information.
Next we start the Integrated Development Environment tool (IDE), which is a fancy word for editor, and we enter programs.
Running and Stopping a Processing Program
Starting a program is simple: just click on the round button with a triangle in it, at the top left of the IDE, and this should start the program.
To stop the program you can either close the graphics window, or click on the round button with a black square in the IDE.
Translating Assembly Examples into Processing |
We saw some very simple examples in assembly language for doing very simple operations. Never-the-less, these simple problems required complex assembly language programs to solve them. We now look at a these same problems, but this time using a "high-level" language: Processing.
Example 1: Sum of 2 variables
- The following program adds the contents of two variables together and stores the resulting sum in a third variable.
void setup() {
int a = 10;
int b = 20;
int c = 0;
c = a + b;
println( "c = " + c );
}
- Some explanations:
- int a indicates that we are creating a variable in memory called a. We are also specifying that it will contain an integer number, which in Processing is called an int. Also, we start the program by storing 10 in variable a.
- Similarly, int b means that we have a variable called b that contains an int. The program starts by storing 20 into b.
- int c, you will have guessed, means that c is also a variable and when the program starts c contains 0.
- The program then adds a to b and stores the result into c.
- Finally the program prints two pieces of information: a sentence "c =", followed by the actual value of c.
Example 2
- This example program generates and prints all the numbers between 1 and 10. It is similar to a program we saw in assembly.
void setup() {
int count = 10;
while ( true ) {
println( count );
count = count - 1;
if ( count == 0 ) break;
}
println( "done!" );
}
- Some explanations:
- The program uses a variable called count that is an integer and contains 10 at that start of the program.
- The next statement is while (true) { ... } which means repeat forever whatever is inside the curly brackets.
- Inside the curly bracket are 3 statements.
- The first one prints the contents of count on the screen
- The second one subtracts 1 from count
- The third one is a tests. It tests if the contents of count are 0, and if so, it forces the program to break out of the while loop.
- If count does not contain 0, then the loop is repeated again, once more.
- If the program breaks out of the loop, it falls automatically on the next statement following the curly bracket of the loop, which prints the sentence "done!" on the screen.
- Here its output:
10 9 8 7 6 5 4 3 2 1 done!
Example 3
- This examples computes the sum of all the numbers from 0 to 10 (included) and stores the result in a variable called sum.
void setup() {
int count = 10;
int sum = 0;
while ( true ) {
sum = sum + count;
count = count - 1;
if ( count == 0 ) break;
}
println( "sum = " + sum );
}
- Hopefully by now you should have enough Processing language under your belt to figure out how the program computes the sum of all the numbers.
- By the way, here's the output of the program:
sum = 55
A First Example Using Graphics |
Assuming that you have Processing installed on your computer, type in the following code in the IDE:
void setup() {
size(480, 480 );
smooth();
}
void draw() {
ellipse(mouseX, mouseY, 80, 80);
}
- Run your program.
- Notice that the program draws circles (ellipses with the same horizontal radius as vertical radius) that overlap each other, following the mouse around.
- When the mouse is outside the window, the graphics window stops moving the circles. This is because the graphics window is sensitive to the mouse only when the mouse is over the window.
Some explanations |
- Once again, a Processing program is called a sketch, and we'll use both terms here interchangeably.
- The sketch contains our two functions: setup() and draw().
- Setup() is executed first and sets the size of the graphics window to 480 pixels wide by 480 pixels high. You can change these around to see how the new window is affected.
- smooth() is called by setup() to make the display of graphics shape smoother to the eye. This will slow down the program a tiny bit, but in most cases, this is something we'll want to do. You can try removing the smooth() call and see how it affect your program.
- The draw() function is listed next. This function is called 30 times a second. All it does is to draw an ellipse at the x and y location of the mouse on the graphics window. Top-left is 0, 0. Bottom right is 479, 479 (since our window size was set to 480, 480).
- And that's it!
This is our first example of animation with Processing. It's easy to do. Just make the draw() function draw something on the graphics window where the mouse is located, and do it 30 times a second. As the mouse moves, the new shapes are drawn following the mouse.
Some Variations to Play with |
Variation #1 |
- Locate the rect() graphics function in Processing's reference section.
- Notice how it should be used:

- Change the ellipse to a rectangle in the sketch as follows:
void setup() {
size(480, 480 );
smooth();
}
void draw() {
// ellipse(mouseX, mouseY, 80, 80);
rect( mouseX, mouseY, 80, 80 );
}
- the two slashes in front of the line with the ellipse() function transforms this line into a comment. A comment is line of code that does not contain any code, and contains textual information that is skipped by the processor when it runs the program.
- The rect() function is asked to use mouseX, and mouseY as the coordinates of where to put the rectangle. The width and height of the rectangle are set to 80 pixels each.
Variation #2 |
- Locate the background() graphics function in Processing's reference section.
- Read the description of the background() function.
- Add a call to the function background() in the draw() function. Pass it the value 200, which is light grey (you would use 0 for full black, and 255 for full white).
void setup() {
size(480, 480 );
smooth();
}
void draw() {
background( 200 );
// ellipse(mouseX, mouseY, 80, 80);
rect( mouseX, mouseY, 80, 80 );
}
- Try the sketch.
- What is happening? Why is there only one rectangle on the screen?
- Comment out the rectangle function by putting two slashes in front of it, and uncomment the ellipse function by removing the two slashes that prefix it. Try the sketch again!
Variation #3 |
- Let's fill the ellipse with a color. This is accomplish with the fill() function.
- Find the description for fill() in the reference section of Processing.org (you know where to go, by now!)
- Add a call to fill() in the draw() function:
void setup() {
size(480, 480 );
smooth();
}
void draw() {
background( 200 );
fill( 150 );
ellipse(mouseX, mouseY, 80, 80);
//rect( mouseX, mouseY, 80, 80 );
}
- Try the sketch!
- If you want to change the color for something more appealing, try this color table: http://web.njit.edu/~kevin/rgb.txt.html
- Pick a color that you like, and copy the three numbers in the third column from the left. Put these numbers in the fill() function, separated by commas. For example, assume you want to use the GreenYellow color:

- Change the fill() function call to read:
- fill( 173, 255, 47 );
- Try it!
Resources |
Best Online Resources
- Processing.org: the Web site for Processing is probably the best place to find information, and to find the language environment which you can download for free.
- Processing.org/learning: good place to start learning Processing, or reviewing concepts seen in class.
- Processing.org/learning/overview: Just what the name says; it's an overview of the language with simple examples.
- Processing.org/reference: the main reference to Processing objects and constructs. The best place to search for new features and find examples of how to use them.
- Another great collection of sketches on openProcessing.org
Searching by Yourself
There is a wealth of Web resources on processing. Unfortunately, when you search for processing on Google (or your favorite search engine), you may get results unrelated to the language Processing, but to the word processing. A good way to force Google to return results that are relevant to the language is to search for processing.org, which is the Web site for Processing.
Good Examples
- The Examples option in the Processing File menu is a good source of many examples illustrating different concepts:
Misc. Videos
|
|
This is less about Processing than about data visualization, and how Ben Fry, one of the co-authors of Processing uses the language to represent data. Several of his projects are presented.
|
|
|
Fry and Reas give a good overview of Processing in the Vimeo movie to the left. This video was filmed before Processing 2 was released, and presents some interesting projects and libraries written for Processing by some of its users. Fry (the first speaker) spends more time on the technology, while Reas presents different projects. |
- Jose Sanchez's list of video tutorials
References |
- ↑ 1.0 1.1 John von Neumann. First Draft of a Report on the EDVAC. IEEE Ann. Hist. Comput. 15, 4 (October 1993), 27-75.
- ↑ Adleman, L. M., "Molecular computation of solutions to combinatorial problems". Science 266 (5187): 1021–1024. 1994.
- ↑ Lewin, D. I., "DNA computing". Computing in Science & Engineering 4 (3): 5–8, 2002.
- ↑ Main, P., "When electrons go with the flow: Remove the obstacles that create electrical resistance, and you get ballistic electrons and a quantum surprise". New Scientist 1887: 30., 1993.
- ↑ Ralston, Anthony; Meek, Christopher, eds., Encyclopedia of Computer Science (second ed.), pp. 488–489, 1976.
- ↑ Algorithm, in Wikipedia, retrieved Oct. 3, 2012, from http://en.wikipedia.org/wiki/Algorithm
- ↑ Steve Lohr, Big Data, Speed, and the Future of Computing, New York Times Technology, Oct 31, 2011.
- ↑ Nate Silver, The Signal and the Noise: Why So Many Predictions Fail-but Some Don't, Penguin, 2012.
- ↑ Moore's Lay, Intel Corporation, 2005. ftp://download.intel.com/museum/Moores_Law/Printed_Material/Moores_Law_2pg.pdf
- ↑ Sundar Iyer, Breaking through the embedded memory bottleneck, part 1, EE Times, July 2012, http://www.eetimes.com/document.asp?doc_id=1279790
- ↑ Samual K. Moore, Multicore is bad news for supercomputers, IEEE Spectrum, Nov. 2008.
- ↑ David R. Henderson and Charles L. Hooper, Making Great Decisions in Business and Life, Chicago Park Press, 1st edition, March 12, 2007.
- ↑ Gordon E. Moore, Cramming More Components onto Integrated Circuits, Electronics, pp. 114–117, April 19, 1965.
- ↑ Tim Worstall, The End of Moore's Law, Forbes, Aug. 29, 2013, http://www.forbes.com/sites/timworstall/2013/08/29/darpa-chief-and-intel-fellow-moores-law-is-ending-soon/, retrieved 9/29/13.
- ↑ C. Reas, B. Fry, Processing: programming for the media arts, AI & Soc (2006) 20: 526–538 DOI 10.1007/s00146-006-0050-9, (http://hlt.media.mit.edu/dfe_readings/processing.pdf)