Difference between revisions of "CSC111 Homework 12 2015"
(→Problem #2) |
|||
| Line 5: | Line 5: | ||
=Problem #1= | =Problem #1= | ||
<br /> | <br /> | ||
| − | Write a program called '''hw12_1.py''' that contains a '''recursive''' function called ''' | + | Write a program called '''hw12_1.py''' that contains a '''recursive''' function called '''smallestLargest()''' which returns the smallest and largest ''elements'' of a list of ''items''. The items may be strings, numbers, or tuples, where the first element of the tuple is either a number or a string. |
Example '''main()''' program: | Example '''main()''' program: | ||
| Line 14: | Line 14: | ||
def main(): | def main(): | ||
A = [ 1, 10, 20, 3, 2, -1, -10, 5, 5, 5, 5 ] | A = [ 1, 10, 20, 3, 2, -1, -10, 5, 5, 5, 5 ] | ||
| − | low, high = | + | low, high = smallestLargest( A ) |
print( "smallest item =", low, " largest item = ", high ) | print( "smallest item =", low, " largest item = ", high ) | ||
# will print | # will print | ||
| Line 20: | Line 20: | ||
A = [ 1 ] | A = [ 1 ] | ||
| − | low, high = | + | low, high = smallestLargest( A ) |
print( "smallest item =", low, " largest item = ", high ) | print( "smallest item =", low, " largest item = ", high ) | ||
# will print | # will print | ||
| Line 26: | Line 26: | ||
A = [ ] | A = [ ] | ||
| − | low, high = | + | low, high = smallestLargest( A ) |
print( "smallest item =", low, " largest item = ", high ) | print( "smallest item =", low, " largest item = ", high ) | ||
# will print | # will print | ||
| Line 32: | Line 32: | ||
A = [ "alpha", "beta", "gamma", "epsilon" ] | A = [ "alpha", "beta", "gamma", "epsilon" ] | ||
| − | low, high = | + | low, high = smallestLargest( A ) |
print( "smallest item =", low, " largest item = ", high ) | print( "smallest item =", low, " largest item = ", high ) | ||
# will print | # will print | ||
| Line 44: | Line 44: | ||
==Requirements== | ==Requirements== | ||
<br /> | <br /> | ||
| − | # The function ''' | + | # The function '''smallestLargest()''' must be recursive. |
# You cannot use the min() or max() standard Python functions. If you want to find the largest of two items, you need to do the comparison in Python, using <, <=, >, or >=. | # You cannot use the min() or max() standard Python functions. If you want to find the largest of two items, you need to do the comparison in Python, using <, <=, >, or >=. | ||
<br /> | <br /> | ||
Revision as of 18:15, 19 April 2015
--D. Thiebaut (talk) 17:30, 19 April 2015 (EDT)
Contents
Problem #1
Write a program called hw12_1.py that contains a recursive function called smallestLargest() which returns the smallest and largest elements of a list of items. The items may be strings, numbers, or tuples, where the first element of the tuple is either a number or a string.
Example main() program:
def main(): A = [ 1, 10, 20, 3, 2, -1, -10, 5, 5, 5, 5 ] low, high = smallestLargest( A ) print( "smallest item =", low, " largest item = ", high ) # will print # smallest item = -10 largest item = 20 A = [ 1 ] low, high = smallestLargest( A ) print( "smallest item =", low, " largest item = ", high ) # will print # smallest item = 1 largest item = 1 A = [ ] low, high = smallestLargest( A ) print( "smallest item =", low, " largest item = ", high ) # will print # smallest item = None largest item = None A = [ "alpha", "beta", "gamma", "epsilon" ] low, high = smallestLargest( A ) print( "smallest item =", low, " largest item = ", high ) # will print # smallest item = alpha largest item = gamma if __name__=="__main__": main()
Requirements
- The function smallestLargest() must be recursive.
- You cannot use the min() or max() standard Python functions. If you want to find the largest of two items, you need to do the comparison in Python, using <, <=, >, or >=.
Submission
Submit your program to the Moodle section, HW12 PB 1
Problem #2
Write a Python program called hw12_2.py that generates, recursively a tree with fruit, as close to the tree shown below as possible. You should not reproduce the text in the image; just the tree, its colors, and its fruit.
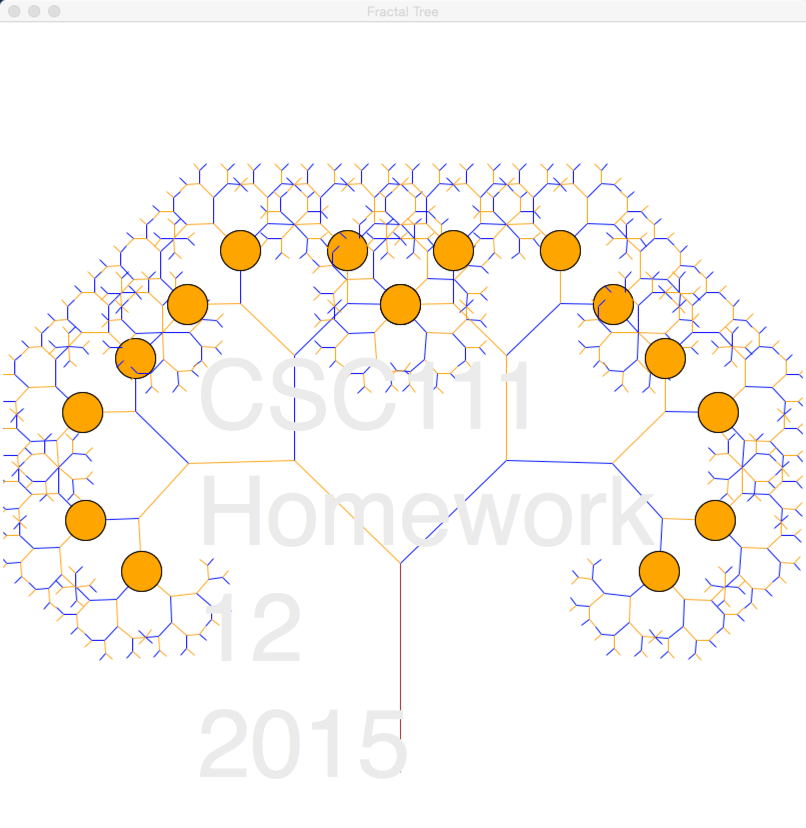
Requirements
- The oranges have a radius of 20. They must be generated inside the recursive function. As a result some of the branches will appear in front, some below the oranges.
- The branches must have different colors, and not be all drawn with the same color.
Submission
- Submit your program as well as a screen capture of its output to Moodle, in the HW12 PB2 and HW12 Image 2 sections.
- Note: To change the color of a line with the graphics library (use graphics111.py, please), you should use the setOutline() method rather than the setFill() method.
- I used only 3 colors to generate the tree above: "orange", "blue", and "brown".
<showafterdate after="20150422 14:00" before="20150601 00:00">
Solution Programs
Recursive MinMax
# hw12_1.py # D. Thiebaut # Solution program for Homework 12 def minmax( A ): """recursive function that returns the min and max of a list of comparable items""" # stopping condition #1 if len( A )==0: return None, None # stopping condition #2 if len( A )==1: return A[0], A[0] # recursive step theMin, theMax = minmax( A[1: ] ) # do a bit of work... if A[0] < theMin: theMin = A[0] if A[0] > theMax: theMax = A[0] # return the smallest or largest of what we kept # and what the recursive call brought back return theMin, theMax def main(): A = [ 1, 10, 20, 3, 2, -1, -10, 5, 5, 5, 5 ] low, high = minmax( A ) print( "smallest item =", low, " largest item = ", high ) # will print # smallest item = -10 largest item = 20 A = [ 1 ] low, high = minmax( A ) print( "smallest item =", low, " largest item = ", high ) # will print # smallest item = 1 largest item = 1 A = [ ] low, high = minmax( A ) print( "smallest item =", low, " largest item = ", high ) # will print # smallest item = None largest item = None A = [ "alpha", "beta", "gamma", "epsilon" ] low, high = minmax( A ) print( "smallest item =", low, " largest item = ", high ) # will print # smallest item = alpha largest item = gamma if __name__=="__main__": main()
Fractal Tree
# fractalTree.py
# D. Thiebaut
# Code taken from http://openbookproject.net/thinkcs/python/english3e/recursion.html
# and adapted to work with graphics111.py.
#
# Draws a fractal tree on the graphic window.
#
from graphics import *
import math
import time
import random
# dimensions of the window
MAXWIDTH = 800
MAXHEIGHT = 800
# recursive tree-drawing function
#
def draw_tree(win , # the canvas
order, # the level of recursion. Starts positive.
theta, # angle of new branch leaving this trunk
sz, # size of this branch
x, y, # coordinates of base of this branch
heading, # angle of direction of this branch
color # color
):
trunk_ratio = 0.29 # How big is the trunk relative to whole tree?
trunk = sz * trunk_ratio # length of trunk
# compute x, y of end of the current branch
delta_x = trunk * math.cos(heading)
delta_y = trunk * math.sin(heading)
x2, y2 = x + delta_x, y + delta_y
# draw current branch
branch = Line( Point( x, y), Point( x2, y2 ) )
branch.setFill( color )
branch.setWidth( 2 )
branch.setOutline( color )
branch.draw( win )
# if this branch has sub-branches, then recurse
if order > 0:
# make the recursive calls to draw the two subtrees
newsz = sz*(1 - trunk_ratio)
draw_tree(win,
order-1, theta, newsz, x2, y2, heading-theta,
"orange" )
draw_tree(win,
order-1, theta, newsz, x2, y2, heading+theta,
"blue" )
# draw orange
if order == 4:
orange = Circle( Point( x, y ), 20 )
orange.setFill( "orange" )
orange.draw( win )
# draw 1 tree in the middle of the screen, shooting straight up.
def main():
win = GraphWin("Fractal Tree", MAXWIDTH, MAXHEIGHT )
theta = 0.8 # use 0.02 for tall skinny trees, 0.7 for fat trees
draw_tree(win,
9,
theta,
MAXWIDTH*0.9, MAXWIDTH//2,
MAXHEIGHT-50,
-math.pi/2,
"brown" )
win.getMouse()
win.close()
main()
</showafterdate>